Trouble moving from multinormal to multi_student_t distribution

Modeling
1

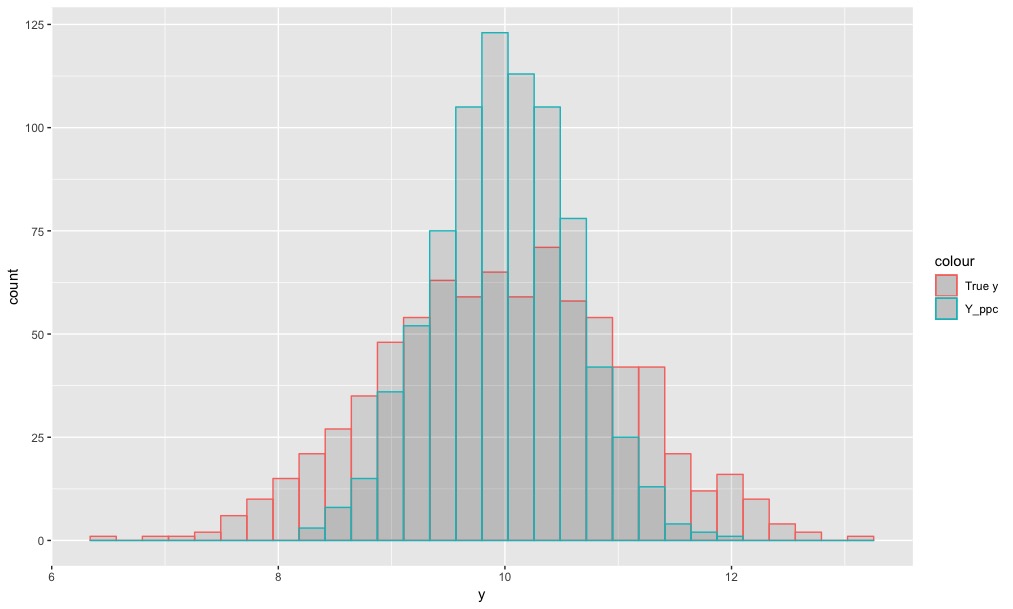
So I have a multi-normal model that behaves pretty well but when I do a posterior predictive check the y_ppc is a bit too confined when compared to the data Y value:

y_ppc_check
y_ppc_check.jpeg1013×609 43.8 KB

I thought I could change this by changing from a multi-normal to a multi_student_t distirbution.I set nu =2 rather than a parameter as I thought this would be an easier fit. However running this model gives me initialisation errors: Initialization between (-2, 2) failed after 100 attempts. z before crashing. I set init = 0 and then it will run but I’m getting almost all divergences.

Can any advise on where I’m going wrong here? I thought I was making a small change to minize issues but it seems not! Code below:

data{
    int<lower=0> NvarsX;  // num independent variables
    int<lower=0> NvarsY;  // num dependent variables
    int<lower=0> N;       // Total number of rows

    matrix[N, NvarsX] x;  // data for independent vars
    vector[NvarsY] y [N]; // data for dependent vars
}

parameters{
    cholesky_factor_corr[NvarsY] L_Omega; //For the correlations between outcome variables
    vector<lower=0>[NvarsY] L_sigma;      //Residual SD of outcome variables

    vector[NvarsY] Beta0;         // Intercepts for each Y
    vector[NvarsX] Beta [NvarsY]; // Coefficients for each X vs each Y
}

transformed parameters{
    vector[NvarsY] mu[N];
    matrix[NvarsY, NvarsY] L_Sigma;

    L_Sigma = diag_pre_multiply(L_sigma, L_Omega);

    for (i in 1:N){
        for (dv in 1:NvarsY){
            mu[i, dv] = Beta0[dv] + dot_product(to_vector(Beta[dv, 1:NvarsX]), x[i, 1:NvarsX]);
        }
    }
}

model{
    //Priors
    L_Omega ~ lkj_corr_cholesky(1);
    L_sigma ~ normal(0, 2.5);
    
    Beta0 ~ normal(0, 3);
    for (dv in 1:NvarsY){
        Beta[dv, 1:NvarsX] ~ normal(0, 2);
    }

    //likelihood
    //y ~ multi_normal_cholesky(mu, L_Sigma);
    y ~ multi_student_t(2, mu, L_Sigma);
}

generated quantities{
    matrix[NvarsY, NvarsY] Omega;
    matrix[NvarsY, NvarsY] Sigma;
    
    vector[NvarsY] mu_ppc[N];       // model predictions for posterior predictive check
    vector[NvarsY] y_ppc [N];       // model predictions for posterior predictive check
    
    // Generate correlation matrix
    Omega = multiply_lower_tri_self_transpose(L_Omega);
    Sigma = quad_form_diag(L_Omega, L_sigma);

    // Generate y_ppc    
    for (n in 1:N){
        for(dv in 1:NvarsY){
            mu_ppc[n, dv] = Beta0[dv] + dot_product(to_vector(Beta[dv, 1:NvarsX]), x[n, 1:NvarsX]);
        }
    }
    //y_ppc = multi_normal_cholesky_rng(mu_ppc, L_Sigma);
    y_ppc = multi_student_t_rng(2, mu_ppc, L_Sigma);
}
2

Why are you replacing a multi_normal_cholesky with just a multi_student_t? The latter takes a covariance matrix, not a Cholesky matrix.

3

Yeah I was just thinking that as I was reviewing the post. Why? Because I’ve nobody to ask except you guys and I prefer to try something before asking a question. It was my best effort.

Ok so is there a cholesky parameterised version of the multi_student_t distribution or I need to rewrite my model for a covariance amtrix in order to use student_t. That would slow things down right?

4

If there is a cholesky-parameterised version of the multi_student_t distribution, it isn’t documented. Probably the simplest thing to do is just to use tcrossprod(L_Sigma) as the third argument of multi_student_t.

1 Like
5

Ok great thanks @jjramsey - much appreciated!! I will try that!

6

That solved my init and divergences problems thanks @jjramsey! It hasn’t sovled my ppc problem but I’ve realised that is due to different Y values having slightly different spread. but thats ok I believe I can address that. Thanks for your help!