I am having some trouble with multi_student_t_rng. I might be misunderstanding something simple about multivariate student t distributions, but I assume that if I set the covariance matrix for the multivariate student t distribution to an eye matrix (i.e. ones on the diagonals, zeros elsewhere), then I am effectively generating a collection of K independent student’s t distributions. To check my understanding, I generated some samples using multi_student_t_rng with nu=5, mu=[0, 0]’, and Sigma=[[1,0],[0,1]]. I also generated some samples with student_t_rng with nu=5, mu=0, and sigma=1.
I expected these samples to have the same distribution. However, it looks like they differ. A density plot of the univariate sample matches the pdf of the student’s t distribution, but the multivariate sample does not appear to do so.
I am hoping I have made some trivial mistake, so I can fix it. Code and results follow, and the jupyter lab notebook export is attached. minimal_student_t.html (614.9 KB)
Can anyone spot and explain my mistake, please?
data {
int nsamp;
real<lower=0> nu;
}
transformed data {
matrix[2,2] S = [[1, 0], [0, 1]];
vector[2] mu = [0, 0]';
}
parameters {}
model {}
generated quantities {
array[nsamp] vector[2] mult_t;
array[nsamp] real uni_t;
mult_t = multi_student_t_rng(nu, rep_array(mu, nsamp), S);
uni_t = student_t_rng(nu, rep_array(0, nsamp), 1);
}
Here are KDE plots of the two variates in the multivariate sample and of the univariate sample, with the student t pdf from scipy.stats.
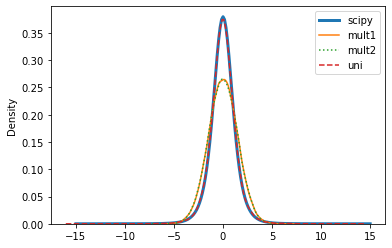
If the colors are hard to see, scipy and uni are on top of each other, and mult1 and mult2 are on top of each other.
