Hi everyone.
I’ve been doing some messing around with the spectral mixture kernel for GP regression. I’ve tried to implement this kernel in Stan, and I’m wondering why I’m struggling to replicate the authors’ results on one of their synthetic examples.
If I’m to attempt a very brief introduction, the spectral mixture kernel aims to represent a stationary covariance structure in terms of its spectral density, which is approximated using a mixture of Q Gaussians.
Expressed in terms of \tau = x_1 - x_2, the kernel itself is:
k(\tau) = \displaystyle\sum_{q=1}^{Q} w_q \exp{(-2 \pi^2 \tau^2\nu_q ) } \cos{(2 \tau \pi \mu_q )}
where the (hyper-)parameters, \mu_q and \nu_q, respectively represent the mean and variance of each of the Q components of the Gaussian mixture used to approximate the spectral density. The weights, w_q, represent the relative contribution of each mixture component.
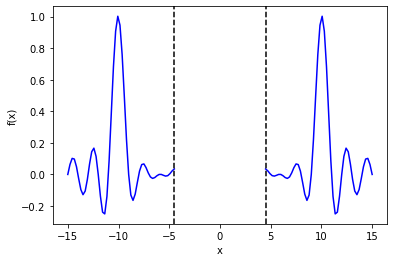
I’m trying to replicate the authors’ example on the “sinc” function, implemented in python as follows:
import numpy as np
sinc = lambda x: np.sin(np.pi * x) / (np.pi * x)
func = lambda x: sinc(x + 10) + sinc(x) + sinc(x - 10)
n = 300
x = np.concatenate([
np.linspace(-15, -4.5, int(n/2)),
np.linspace(4.5, 15, int(n/2))]
)
y = func(x)
The aim is to predict the value of the function between -4.5 and 4.5, given data outside of this region:
My (rather crude) Stan model is:
functions {
matrix L_cov_sm(vector x, vector mu, vector nu, vector w, real jitter, int N, int Q) {
matrix[N, N] C;
real tau;
real tmp;
for (i in 1:N){
for (j in 1:i){
tau = abs(x[i] - x[j]);
tmp = 0;
for (q in 1:Q){
tmp += w[q] * exp(-2 * square(pi()) * square(tau) * nu[q]) * cos(2 * tau * pi() * mu[q]);
}
if (i == j) {tmp += jitter;}
C[i, j] = tmp;
C[j, i] = tmp;
}
}
return cholesky_decompose(C);
}
}
data {
int<lower=1> N;
int<lower=1> Q;
vector[N] x;
vector[N] y;
real<lower=0> jitter;
}
parameters {
vector<lower=0>[Q] nu;
vector[Q] mu;
vector<lower=0>[Q] w;
}
transformed parameters {
matrix[N, N] L;
vector[N] meanv;
L = L_cov_sm(x, mu, nu, w, jitter, N, Q);
meanv = rep_vector(0, N);
}
model {
w ~ cauchy(0, 5);
mu ~ cauchy(0, 5);
nu ~ normal(0, 1);
y ~ multi_normal_cholesky(meanv, L);
}
Which, for the sake of providing a complete example, I’m running through pystan using:
import pystan
import multiprocessing
multiprocessing.set_start_method("fork")
Q = 10
data = {
'x': x,
'y': y,
'N': x.shape[0],
'Q': Q,
'jitter': 1e-10,
}
ret = smgp_sm.optimizing(data) # the model from before
As far as I can tell, the authors do not discuss prior distributions for any of the kernel parameters (the distributions for \mu, \nu and w you’re seeing in my model are an attempt to get the optimiser to behave better, though I suspect they’re still too vague to have much – if any – influence), and use gradient based optimisation to maximise the log likelihood.
I’ve been attempting to do the same using Stan’s optimiser.
I am occasionally getting sensible looking results using (the default) l-bfgs, and less occasionally getting sensible results using method='Newton'. I’m unsure whether the inconsistency I’m experiencing is due to just initialisation or initialisation and some kind of modelling error somewhere, as even when the posterior predictive distribution of the GP looks “about right” (I can include the code I use to do this if it’s valuable, but it’s pretty generic GP regression stuff), my values for \mu do not match the authors’.
I would really appreciate it if anyone with experience using this kernel could:
- a) Sanity check my model, and/or:
- b) Provide any advice on initialising the parameters.
I’ll add that my intention with this exercise was as a stepping stone to messing around with full sample-based inference of the kernel parameters, so any further advice or comments on specifying priors for \mu, \nu and w would be welcome, too: I know from a few experiments that some re-parametrisation is going to be necessary, but I’m not really sure where to start.
Thanks for reading!