Hi, I’m new to Stan and my model can not converge.
Here’s a brief introduction to my model.
I need to estimate the mortality rate for 21 countys in 21 years (1995~2015). Thus the data is one 21x21 matrix for births x and one for deaths y.
So denote underlying mortality rate as Alpha, this is a binomial distribution with y \sim binomial(x, Alpha). And it is obvious that the mortality rate should be quite small, say 96 deaths out of 22626.
For Alpha, I use a bayesian penalized spline regression model. The original model is shown in this picture (cut from the paper I read).
I did a little change to this original model.
-
\Psi in this original model is the log transformation of true mortality rate. Yet I found that when calculating true rate, \exp(\Psi) are not constrained in [0,1]. So I modeled \Psi as the logit transformation of true rate.
-
The original model has different sources of data, and my data is quite simple, so I simplified the data model part to
\delta_c \sim N(0, \nu_c), \nu_c \sim U(1, 10), suggesting that different county has different variation.
Here’s my stan code.
data {
int TT; // number of years, 21
int K; // number of splines, 13
int C; // number of countys, 21
real I; // between-knot intervals, set to 2.5 years
int x[C,TT]; // births
int y[C,TT]; // deaths
matrix[K,K-2] D_Kc; // transformation of difference matrix
matrix[TT,K] B; // calculated cubic spline matrix
}
parameters {
real chi;
real<lower=0> phi;
real sigma_lg[C];
real<lower=0> lambda_0_exp[C];
vector[C] lambda_1_unit;
real<lower=0> nu[C];
matrix[C,K-2] epsilon;
row_vector[TT] delta[C];
}
transformed parameters {
real<lower=0> sigma[C];
real lambda_0[C];
vector[C] lambda_1;
row_vector[K] alpha[C]; // spline coefficients
sigma = exp(sigma_lg);
lambda_0 = log(lambda_0_exp);
lambda_1 = lambda_1_unit * I;
for (c in 1:C){
for (k in 1:K)
alpha[c,k] = lambda_0[c] + lambda_1[c] * (k - K * 1.0 / 2) + D_Kc[k] * epsilon[c]';
}
}
model {
chi ~ normal(-3, sqrt(10));
phi ~ uniform(0,5);
sigma_lg ~ normal(chi, phi);
lambda_0_exp ~ uniform(1,1000);
lambda_1_unit ~ uniform(-0.25, 0.2);
nu ~ uniform(1, 10);
for (c in 1:C){
delta[c] ~ normal(0, nu[c]);
epsilon[c] ~ normal(0, sigma[c]);
target += binomial_logit_lpmf( y[c] | x[c] , exp(alpha[c] * B' + delta[c]) );
}
}
generated quantities {
row_vector<lower=0, upper=1>[TT] Alpha[C]; // estimated true mortality rate
for (c in 1:C)
Alpha[c] = inv_logit(alpha[c] * B' + delta[c]);
}
Here’s my R code.
library(bdefdata)
library(demest)
library(dplyr)
library(purrr)
library(tidyr)
library(boot)
library(latticeExtra)
library(rstan)
library(splines)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
y <- bdefdata::sweden_deaths
x <- bdefdata::sweden_births
C <- dim(x)[1]
TT <- dim(x)[2]
tpower <- function(x, t, p){
# Truncated p-th power function
(x - t) ^ p * (x > t)
}
bbase <- function(x, xl, xr, dx, deg){
# Construct a B-spline basis of degree ’deg’
knots <- seq(xl - deg * dx, xr + deg * dx, by = dx)
P <- outer(x, knots, tpower, deg)
n <- dim(P)[2]
D <- diff(diag(n), diff = deg + 1) / (gamma(deg + 1) * dx ^ deg)
B <- (-1) ^ (deg + 1) * P %*% t(D)
B
}
B <- round(bbase(1995:2015, 1995, 2015, 2.5, 3), 8)
K <- dim(B)[2]
I <- 2.5
D <- matrix(rep(0, (K-2)*K), nrow=K-2)
for (i in 1:K-2){
for (j in 1:K){
if (i == j | j == i + 2) D[i,j] = 1
if (j == i + 1) D[i,j] = -2
}
}
D_Kc <- t(D) %*% solve(D %*% t(D))
d <- list(C=C,
TT=TT,
K=K,
I=I,
x=x,
y=y,
D_Kc=D_Kc,
B=B)
set.seed(12)
initf <- function(chain_id){
list(lambda_0_exp = runif(C, 1, 1000),
lambda_1_unit = runif(C, -0.25, 0.2),
nu = runif(C, 1, 10),
epsilon = matrix(rnorm(C*(K-2), 0, 1), nrow=C)
)
}
n_chains <- 6
a <- lapply(1:n_chains, function(id) initf(chain_id = id))
f <- stan(file = 'mr.stan', data = d, chains = n_chains,
iter = 50000, warmup = 10000, thin = 10,
control = list(adapt_delta = 0.9),
init = a)
And the 6 chains do not converge. Warning message suggests “divergent transitions after warmup”, which is almost all of them.
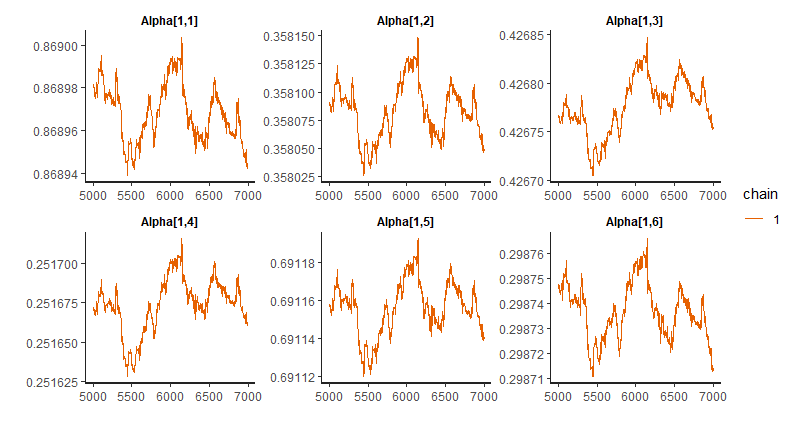
Here’s the traceplot of several Alpha.
Here’s another traceplot of another run with only one chain.
> sessionInfo()
R version 3.5.3 (2019-03-11)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 18362)
Matrix products: default
locale:
[1] LC_COLLATE=Chinese (Simplified)_China.936
[2] LC_CTYPE=Chinese (Simplified)_China.936
[3] LC_MONETARY=Chinese (Simplified)_China.936
[4] LC_NUMERIC=C
[5] LC_TIME=Chinese (Simplified)_China.936
attached base packages:
[1] splines stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] rstan_2.19.3 ggplot2_3.2.1 StanHeaders_2.19.0
[4] latticeExtra_0.6-28 RColorBrewer_1.1-2 lattice_0.20-38
[7] boot_1.3-23 tidyr_1.0.0 purrr_0.3.2
[10] dplyr_0.8.3 demest_0.0.0.202 dembase_0.0.0.108
[13] bdefdata_0.0.0.9002
I really need some suggestions. And if there’s naive mistakes in my code, please point them out. Thanks for your time : )