Hello!
I am trying to use stan to build mortality models that can be applied to multiple adjacent areas at the same time.
firstly, I have tried the following mortality model and this works well on my computer.
data {
int<lower=0> T; // number of years
int<lower=0> A; // number of age categories
int<lower=0> Tf; // number of forecast years
array[A*T] int<lower=0> death; // deaths
array[A*T] real<lower=0> expos; // exposures
}
transformed data {
array[A*T] real loge = log(expos); // log exposures
int<lower = 1> J = T + A - 1;
}
parameters {
vector[A] a; // alpha_x
simplex[A] b1; // beta_x, strictly positive and sums to 1
simplex[A] b2;
vector[T-2] ks; // vector of k_t differences
vector[J-3] gs;
real c1;
real c2;
real psi;
real<lower = 0> sigma_k; // standard deviation of the random walk
real<lower = 0> sigma_g;
}
transformed parameters {
vector[T] k;
vector[J] g;
array[A*T] real logm;
k[1] = 0;
k[2] = -sum(ks[1:(T-2)]);
k[3:T] = ks;
g[1] = 0;
g[J] = 0;
g[2] = -sum(gs[1:(J-3)]);
g[3:(J-1)] = gs;
for (j in 1:T) for (i in 1:A) {
logm[A*(j-1)+i] = loge[A*(j-1)+i] + a[i] + b1[i] * k[j] + b2[i] * g[j-i+A];
}
}
model {
target += poisson_log_lpmf(death| logm);
target += normal_lpdf(ks[1]| c1, sigma_k);
target += normal_lpdf(ks[2:(T-2)]| c1 + ks[1:(T-3)], sigma_k);
target += normal_lpdf(gs[1]|c2 + psi * (- c2),sigma_g);
target += normal_lpdf(gs[2]|c2 + gs[1] + psi * (- gs[1] - c2),sigma_g);
target += normal_lpdf(gs[3:(J-3)]|c2 + gs[2:(J-4)] + psi * (gs[2:(J-4)] - gs[1:(J-5)] - c2),sigma_g);
target += normal_lpdf(a|0,10);
target += normal_lpdf(c1|0,sqrt(10));
target += normal_lpdf(c2|0,sqrt(10));
target += normal_lpdf(psi|0,sqrt(10));
target += dirichlet_lpdf(b1|rep_vector(1, A));
target += dirichlet_lpdf(b2|rep_vector(1, A));
target += student_t_lpdf(sigma_k|4, 0, 1);
target += student_t_lpdf(sigma_g|4, 0, 1);
}
generated quantities {
vector[Tf] k_p;
vector[Tf] alpha_k_p;
vector[Tf] delta_k_p;
vector[Tf] g_p;
vector[T+Tf+A-1] g_f;
vector[A*Tf] mfore; // predicted death rates
vector[A*T] log_lik;
array[A*T] real m;
int pos1 = 1;
k_p[1] = c1 + k[T] + sigma_k * normal_rng(0,1);
for (t in 2:Tf){
k_p[t] = c1 + k_p[t-1] + sigma_k * normal_rng(0,1);
}
g_p[1] = c2 + g[J] + psi * (g[J] - g[J-1] - c2) + sigma_g * normal_rng(0,1);
g_p[2] = c2 + g_p[1] + psi * (g_p[1] - g[J] - c2) + sigma_g * normal_rng(0,1);
for (t in 3:Tf){g_p[t] = c2 + g_p[t-1] + psi * (g_p[t-1] - g_p[t-2] - c2) + sigma_g * normal_rng(0,1);}
g_f = append_row(g, g_p);
for (t in 1:Tf) for (i in 1:A) {
mfore[pos1] = exp(a[i] + b1[i] * k_p[t] + b2[i] * g_f[T+t-i+A]);
pos1 += 1;
}
for(i in 1:A*T){
m[i] = exp(logm[i] - loge[i]);
log_lik[i] = poisson_log_lpmf(death[i]|logm[i]);
}
}
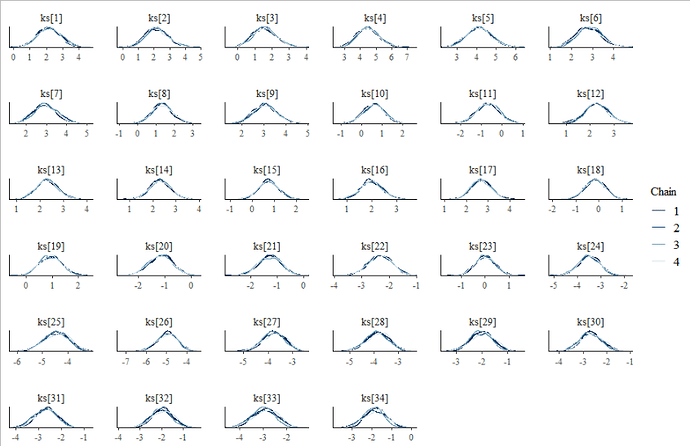
The following images show the model converges even with a short number of iterations(iter_warmup = iter_sampling = 1000).
I then tried to extend the model, and at the beginning I tried to apply the exact same model as before to P different regions.
data {
int<lower=0> T; // number of years
int<lower=0> A; // number of age categories
int<lower=0> P; // number of regions
int<lower=0> Tf; // number of forecast years
array[A*T*P] int<lower=0> death; // deaths
array[A*T*P] real<lower=0> expos; // exposures
}
transformed data {
array[A*T*P] real loge = log(expos); // log exposures
int AT = A*T;
int ATP = AT*P;
int<lower=0> J = T+A-1;
}
parameters {
array[P] vector[A] ap;
array[P] simplex[A] bp1;
array[P] simplex[A] bp2;
array[P] vector[T-2] kps;
array[P] vector[J-3] gps;
array[P] real cp1;
array[P] real cp2;
array[P] real psip;
array[P] real<lower = 0> sigma_kp;
array[P] real<lower = 0>sigma_gp;
}
transformed parameters {
array[P] vector[T] kp;
array[P] vector[J] gp;
array[ATP] real logm;
for(p in 1:P){
kp[p][1] = 1;
kp[p][2] = -sum(kps[p][1:(T-2)]);
kp[p][3:T] = kps[p];
gp[p][1] = 0;
gp[p][2] = -sum(gps[p][1:(J-3)]);;
gp[p][3:(J-1)] = gps[p];
gp[p][J] = 0;
}
for (p in 1:P) for (j in 1:T) for (i in 1:A) {
logm[AT*(p-1) + A*(j-1) + i] = loge[AT*(p-1) + A*(j-1) + i] +
ap[p][i] + bp1[p][i] * kp[p][j] + bp2[p][i] * gp[p][j-i+A];
}
}
model {
for(p in 1:P){
target += normal_lpdf(kps[p][1]| cp1[p], sigma_kp[p]);
target += normal_lpdf(kps[p][2:(T-2)]| cp1[p] + kps[p][1:(T-3)], sigma_kp[p]);
target += normal_lpdf(gps[p][1]|cp2[p] + psip[p] * (-cp2[p]), sigma_gp[p]);
target += normal_lpdf(gps[p][2]|cp2[p] + gps[p][1] + psip[p] * (gps[p][1] - cp2[p]), sigma_gp[p]);
target += normal_lpdf(gps[p][3:(J-3)]|cp2[p] + gps[p][2:(J-4)] + psip[p] * (gps[p][2:(J-4)] - gps[p][1:(J-5)] - cp2[p]), sigma_gp[p]);
target += normal_lpdf(ap[p]|0,10);
target += dirichlet_lpdf(bp1[p]|rep_vector(1, A));
target += dirichlet_lpdf(bp2[p]|rep_vector(1, A));
target += normal_lpdf(cp1[p]|0,sqrt(10));
target += normal_lpdf(cp2[p]|0,sqrt(10));
target += normal_lpdf(psip[p]|0,sqrt(10));
target += student_t_lpdf(sigma_kp[p]|4, 0, 1);
target += student_t_lpdf(sigma_gp[p]|4, 0, 1);
}
}
generated quantities {
array[P] vector[Tf] kp_p;
array[P] vector[Tf] gp_p;
array[P] vector[T+Tf+A-1] gp_f;
vector[A*Tf*P] mfore; // predicted death rates
vector[ATP] log_lik;
array[ATP] real m;
int pos1 = 1;
for(p in 1:P){
kp_p[p][1] = cp1[p] + kp[p][T] + sigma_kp[p] * normal_rng(0,1);
for (t in 2:Tf){kp_p[p][t] = cp1[p] + kp_p[p][t-1] + sigma_kp[p] * normal_rng(0,1);}
gp_p[p][1] = cp2[p] + gp[p][J] + psip[p] * (gp[p][J] - gp[p][J-1] - cp2[p]) + sigma_gp[p] * normal_rng(0,1);
gp_p[p][2] = cp2[p] + gp_p[p][1] + psip[p] * (gp_p[p][1] - gp[p][J] - cp2[p]) + sigma_gp[p] * normal_rng(0,1);
for (t in 3:Tf){gp_p[p][t] = cp2[p] + gp_p[p][t-1] + psip[p] * (gp_p[p][t-1] - gp_p[p][t-2] - cp2[p]) + sigma_gp[p] * normal_rng(0,1);}
gp_f[p] = append_row(gp[p], gp_p[p]);
}
for (p in 1:P) for (j in 1:Tf) for (i in 1:A) {
mfore[pos1] = exp(ap[p][i] + bp1[p][i] * kp_p[p][j] + bp2[p][i] * gp_f[p][T+j-i+A]);
pos1 += 1;
}
for(i in 1:ATP){
m[i] = exp(logm[i] - loge[i]);
log_lik[i] = poisson_log_lpmf(death[i]|logm[i]);
}
}
However, this model is extremely slow and does not converge when the data is very large (170892 pairs of deaths and expos data). So I tried to experiment with fewer data first.
I believe that this model should produce similar results to the former when P = 1 and the data used are the same. But it still fails to converge.
Is there something wrong with my coding or is there some feature of stan that I am not known?
Any help or comments are greatly needed, thanks.