This is a follow-up question from my previous post.
I would basically like to examine the effects of a predictor on the differences between two proportions (\frac{n_1}{N_1} - \frac{n_2}{N_2}). The input data are the four count variables from which to calculate the two proportions (n_1, N_1, n_2, N_2) and a predictor variable (x).
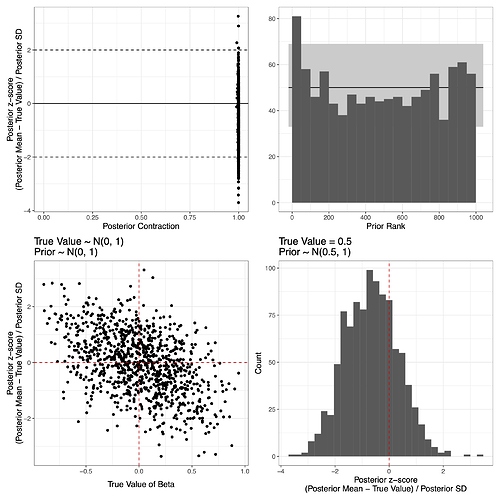
Based on the suggestions I received on my previous post, I am trying to follow @betanalpha’s simulation-based calibration and a principled Bayesian workflow as explained in Schad et al. (2020), and found that even though the model overall may look acceptable (I’m actually not very sure of this – Do extremely high contraction ratios in the upper left panel in the figure below suggest something like I should use a more informative prior?), there is a negative correlation (r = -0.47) between the true values of beta (i.e., slope for x) and the bias, as shown in the lower left panel.
I thought it might be because the prior is dragging the posterior towards 0, so I tested it again with a fixed true value (0.5) and the prior whose mean is the fixed value. As shown in the lower right panel, however, the bias still remains. An even more strongly negative correlation between bias and true values (r = -0.65) is observed in the intercept parameter (figure not shown).
I am wondering if there is a way to figure out possible reasons for the correlation and bias, and how I can go about fixing them.
Here is the Stan code used (identical to the code in my earlier post):
data {
int<lower=0> N; // total number of observations
int<lower=1> denom1[N]; // denominator of the first proportion
int<lower=1> denom2[N]; // denominator of the second proportion
int<lower=0> nom1[N]; // nominator of the first proportion
int<lower=0> nom2[N]; // nominator of the second proportion
real x[N]; // predictor variable
}
parameters {
real<lower=0, upper=1> theta1[N]; // the first proportion
real<lower=0, upper=1> theta2[N]; // the second proportion
real alpha; // intercept
real beta; // slope parameter for x
real<lower=0> sigma; // SD of the error term
}
transformed parameters {
real<lower=-1, upper=1> deltaP[N]; // Delta P
for (i in 1:N) {
deltaP[i] = theta1[i] - theta2[i];
}
}
model {
// priors
theta1 ~ beta(1, 1);
theta2 ~ beta(1, 1);
alpha ~ normal(0, 1);
beta ~ normal(0, 1); //beta ~ normal(0.5, 1); for the lower right panel
sigma ~ normal(0, 1) T[0, ];
for (i in 1:N) {
// estimating thetas based on denoms and noms
nom1[i] ~ binomial(denom1[i], theta1[i]);
nom2[i] ~ binomial(denom2[i], theta2[i]);
// deltaP is sampled from the truncated normal distribution whose mean is alpha + beta * x and the SD is sigma
deltaP[i] ~ normal(alpha + beta * x[i], sigma) T[-1, 1];
}
}
And here is the R cod used to perform simulation:
library("rstan")
library("brms")
# number of simultations
nsim <- 1000
# sample size per simulation
N <- 100
alpha_cf <- beta_cf <- sigma_cf <- Rhats <- div_trans <- neffRatio <- sbc_rank <- z_score <- contraction <- sbc_rank_alpha <- z_score_alpha <- contraction_alpha <- numeric(nsim)
x_cf <- deltaP_cf <- theta1_cf <- theta2_cf <- denom1_cf <- denom2_cf <- nom1_cf <- nom2_cf <- vector("list", nsim)
t <- proc.time()
for (j in 1:nsim) {
set.seed(j)
while (TRUE) {
# predictor values
x_cf[[j]] <- runif(N, -1, 1)
# True parameter values
alpha_cf[j] <- rnorm(1, 0, 1)
beta_cf[j] <- rnorm(1, 0, 1) # 0.5 for the lower right panel
sigma_cf[j] <- abs(rnorm(1, mean = 0, sd = 1))
deltaP_cf[[j]] <- alpha_cf[j] + beta_cf[j] * x_cf[[j]] + rnorm(N, sd = sigma_cf[j])
if (all(deltaP_cf[[j]] <= 1) & all(deltaP_cf[[j]] >= -1)) break
}
# theta values
theta1_cf[[j]] <- theta2_cf[[j]] <- numeric(N)
for (i in 1:N) {
if (deltaP_cf[[j]][i] > 0) {
theta1_cf[[j]][i] <- runif(1, deltaP_cf[[j]][i], 1)
theta2_cf[[j]][i] <- theta1_cf[[j]][i] - deltaP_cf[[j]][i]
} else {
theta2_cf[[j]][i] <- runif(1, abs(deltaP_cf[[j]][i]), 1)
theta1_cf[[j]][i] <- theta2_cf[[j]][i] + deltaP_cf[[j]][i]
}
}
# denoms and noms
denom1_cf[[j]] <- sample(10:100, size = N, replace = TRUE)
denom2_cf[[j]] <- sample(10:100, size = N, replace = TRUE)
nom1_cf[[j]] <- rbinom(N, denom1_cf[[j]], theta1_cf[[j]])
nom2_cf[[j]] <- rbinom(N, denom2_cf[[j]], theta2_cf[[j]])
### fit the model
fit_cf <- sampling(model_cf,
data = list(
N = N,
denom1 = denom1_cf[[j]],
denom2 = denom2_cf[[j]],
nom1 = nom1_cf[[j]],
nom2 = nom2_cf[[j]],
x = x_cf[[j]]
))
# extracting/calculating metrics indicating convergence issues
Rhats[j] <- rhat(fit_cf, pars = "beta")
div_trans[j] <- sum(subset(nuts_params(fit_cf), Parameter == "divergent__")$Value)
neffRatio[j] <- neff_ratio(fit_cf, pars = "beta")
## Slope parameter
# posterior
beta_post <- posterior_samples(fit_cf, pars = "beta")
thinned.pos <- seq(1, nrow(beta_post), 4) # thin to remove autocorrelation
sbc_rank[j] <- sum(beta_cf[j] < beta_post$beta[thinned.pos])
# sensitivity
post_mean_beta <- mean(beta_post$beta)
post_sd_beta <- sd(beta_post$beta) # posterior sd
z_score[j] <- (post_mean_beta - beta_cf[j]) / post_sd_beta
contraction[j] <- 1 - (post_sd_beta^2 / 1^2)
## Do the same for the intercept parameter
alpha_post <- posterior_samples(fit_cf, pars = "alpha")
thinned.pos_alpha <- seq(1, nrow(alpha_post), 4)
sbc_rank_alpha[j] <- sum(alpha_cf[j] < alpha_post$alpha[thinned.pos_alpha])
post_mean_alpha <- mean(alpha_post$alpha)
post_sd_alpha <- sd(alpha_post$alpha) # posterior sd
z_score_alpha[j] <- (post_mean_alpha - alpha_cf[j]) / post_sd_alpha
contraction_alpha[j] <- 1 - (post_sd_alpha^2 / 1^2)
}