I would like to know if anyone has translated an example from Bayesian Data Analysis (3rd edition) to Stan. That example is Stratified sampling in pre-election polling, chapter 8, page 207. I know that there is a repository where you can find examples from BDA3 in Stan (here, but there are no examples from chapter 8) and I could do that, but I prefer to ask before I begin.
Let’s begin with the nonhierarchical model. I will be using python. If you want to follow along with the code, first go here and download the file as .txt. I called it cbs_survey.txt.
Import some libraries:
import numpy as np
import matplotlib.pyplot as plt
import pystan
import pandas as pd
plt.style.use('seaborn-darkgrid')
plt.rc('font', size=12)
It is a survey of 1447 people, so:
participants = 1447
data = pd.read_csv('cbs_survey.txt', sep=' ', skiprows=2, skipinitialspace=True, index_col=False)
print(data)
We need the number of people of each region and each candidate.
data_obs = data[['bush', 'dukakis', 'other']].to_numpy()
print(data_obs)
And a variable called proportion:
proportion = data['proportion'].to_numpy() * participants
print(proportion)
And another variable:
valores = data_obs[:, :] * proportion.reshape(16, -1)
valores = np.round(valores)
np.sum(valores) # Check if the sum is equal to 1447
Now, Stan
model_non_hier="""
data {
int<lower=0> N;
int<lower=0> n;
int y_obs[N, n];
vector[n] alpha;
}
parameters {
simplex[n] theta[N];
}
model {
for (i in 1:N)
theta[i] ~ dirichlet(alpha);
for (i in 1:N)
y_obs[i] ~ multinomial(theta[i]);
}
"""
Now:
stan_model = pystan.StanModel(model_code=model_non_hier)
data2 = {'N': 16,
'n': 3,
'alpha': [1,1,1],
'y_obs': valores.astype(int)}
fit = stan_model.sampling(data=data2)
The output is very long.
print(fit.stansummary(digits_summary=5))
Inference for Stan model: anon_model_2a28c5090c429737936718a5aee45413.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta[1,1] 0.3007 0.0006 0.0643 0.1805 0.2566 0.2987 0.3413 0.4357 8933 0.9995
theta[2,1] 0.4902 0.0008 0.0726 0.3454 0.4426 0.4907 0.5382 0.6296 7457 0.9997
theta[3,1] 0.4648 0.0003 0.0379 0.3918 0.4387 0.4640 0.4902 0.5415 9417 0.9995
theta[4,1] 0.4587 0.0006 0.0566 0.3484 0.4198 0.4589 0.4974 0.5708 7798 0.9993
theta[5,1] 0.4011 0.0007 0.0690 0.2691 0.3541 0.3999 0.4479 0.5394 9671 0.9993
theta[6,1] 0.4424 0.0005 0.0510 0.3418 0.4083 0.4422 0.4758 0.5441 8823 0.9992
theta[7,1] 0.5041 0.0005 0.0467 0.4125 0.4723 0.5041 0.5361 0.5958 8730 0.9993
theta[8,1] 0.5474 0.0004 0.0412 0.4684 0.5191 0.5470 0.5772 0.6272 7904 0.9992
theta[9,1] 0.5420 0.0011 0.0984 0.3488 0.474 0.5443 0.6117 0.7277 7048 0.9994
theta[10,1] 0.4640 0.0005 0.0495 0.3675 0.4304 0.4641 0.4974 0.5617 8140 0.9994
theta[11,1] 0.5103 0.0006 0.0491 0.4110 0.4786 0.5098 0.5430 0.6038 6471 1.0000
theta[12,1] 0.5513 0.0004 0.0357 0.4815 0.5270 0.5506 0.5749 0.6215 7018 0.9993
theta[13,1] 0.4868 0.0008 0.0796 0.3304 0.4328 0.4865 0.5421 0.6381 8040 0.9992
theta[14,1] 0.5245 0.0006 0.0550 0.4146 0.4872 0.5255 0.5615 0.6307 7609 0.9998
theta[15,1] 0.5362 0.0004 0.0438 0.4496 0.5067 0.5373 0.5662 0.6197 9523 0.9996
theta[16,1] 0.5467 0.0005 0.0553 0.4364 0.5082 0.5471 0.5851 0.6519 8899 0.9997
theta[1,2] 0.5990 0.0008 0.0698 0.4569 0.5527 0.6008 0.6479 0.7298 7472 0.9993
theta[2,2] 0.4687 0.0008 0.0729 0.3284 0.4189 0.4679 0.5171 0.6174 7076 0.9997
theta[3,2] 0.4118 0.0004 0.0377 0.3386 0.3867 0.4115 0.4376 0.4858 8076 0.9997
theta[4,2] 0.5137 0.0006 0.0574 0.4014 0.4739 0.5140 0.5538 0.6282 7946 0.9994
theta[5,2] 0.4793 0.0007 0.0693 0.3462 0.4325 0.4794 0.5265 0.6144 8717 0.9993
theta[6,2] 0.4439 0.0005 0.0504 0.3453 0.4107 0.4431 0.4768 0.5447 8078 0.9993
theta[7,2] 0.3863 0.0004 0.0447 0.2973 0.3561 0.3854 0.4156 0.4760 8224 0.9993
theta[8,2] 0.3377 0.0004 0.0393 0.2636 0.3094 0.3373 0.3652 0.4153 7598 0.9993
theta[9,2] 0.2921 0.0010 0.0896 0.1357 0.2273 0.2865 0.3510 0.4831 7374 0.9993
theta[10,2] 0.4042 0.0005 0.0490 0.3086 0.3713 0.4038 0.4377 0.4997 7401 0.9997
theta[11,2] 0.4014 0.0006 0.0489 0.3059 0.3680 0.4007 0.4339 0.5005 6078 0.9996
theta[12,2] 0.3511 0.0004 0.0350 0.2808 0.3278 0.3510 0.3736 0.4225 7039 0.9996
theta[13,2] 0.4595 0.0009 0.0794 0.3089 0.4043 0.4587 0.5137 0.6184 7402 0.9993
theta[14,2] 0.3507 0.0006 0.0542 0.2478 0.3126 0.3489 0.3875 0.4623 8022 0.9994
theta[15,2] 0.3691 0.0004 0.0427 0.2854 0.3405 0.3685 0.3975 0.4549 7822 0.9995
theta[16,2] 0.3600 0.0005 0.0532 0.2594 0.3234 0.3589 0.3969 0.4663 8431 0.9996
theta[1,3] 0.1002 0.0004 0.0423 0.0333 0.0692 0.0952 0.1255 0.1975 7723 0.9993
theta[2,3] 0.0410 0.0003 0.0285 0.0051 0.0201 0.0347 0.0552 0.1128 6573 0.9999
theta[3,3] 0.1233 0.0002 0.0246 0.0793 0.1056 0.1223 0.1395 0.1750 8132 0.9999
theta[4,3] 0.0275 0.0002 0.0188 0.0032 0.0135 0.0236 0.0370 0.0749 6783 0.9997
theta[5,3] 0.1195 0.0005 0.0449 0.0459 0.0864 0.1152 0.1466 0.2226 8130 0.9995
theta[6,3] 0.1135 0.0003 0.0321 0.0577 0.0904 0.1112 0.1334 0.1824 7675 0.9992
theta[7,3] 0.1095 0.0003 0.0292 0.0603 0.0880 0.1073 0.1281 0.1701 7200 0.9994
theta[8,3] 0.1147 0.0003 0.0256 0.0689 0.0966 0.1132 0.1315 0.1691 7493 0.9994
theta[9,3] 0.1658 0.0009 0.0735 0.0503 0.1113 0.1582 0.2113 0.3322 6146 0.9995
theta[10,3] 0.1317 0.0004 0.0340 0.0724 0.1076 0.1297 0.1528 0.2042 7260 0.9997
theta[11,3] 0.0881 0.0003 0.0282 0.0409 0.0676 0.0855 0.1058 0.1517 7555 0.9993
theta[12,3] 0.0975 0.0002 0.0226 0.0583 0.0815 0.0959 0.1120 0.1456 6503 0.9997
theta[13,3] 0.0535 0.0004 0.0371 0.0060 0.0262 0.0458 0.0723 0.1464 6138 0.9994
theta[14,3] 0.1247 0.0004 0.0364 0.0619 0.0987 0.1217 0.148 0.2014 6789 0.9994
theta[15,3] 0.0946 0.0003 0.0266 0.0490 0.0754 0.0919 0.1113 0.1525 7251 0.9991
theta[16,3] 0.0932 0.0003 0.0315 0.0409 0.0706 0.0900 0.1123 0.1651 7889 0.9993
lp__ -1.4149e3 0.1127 4.2446-1.4241e3-1.4175e3-1.4145e3-1.4118e3-1.4076e3 1418 1.0038
Samples were drawn using NUTS at Tue Jul 30 17:33:35 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
Let’s reproduce Figure 8.1(a).
samples = fit.extract(permuted=True)['theta']
print(sample.shape)
diff3 = []
for i in range(16):
result3 = samples[:, i, 0] - samples[:, i, 1]
diff3.append(list(result3))
diff3 = np.asarray(diff3)
res3 = np.sum(diff3.T * proportion / np.sum(proportion), axis=1)
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(res3, bins=20, edgecolor='w', density=True)
plt.show()
Nice!
Now the book goes to the hierarchical model (page 209).
As an aid to constructing a reasonable model, we transform the parameters to separate
partisan preference and probability of having a preference:\alpha_{1j} = \dfrac{\theta_{1j}}{\theta_{1j} + \theta_{2j}},
\alpha_{2j} = 1 - \theta_{3j}.
To get \alpha_{1j} and \alpha_{2j}:
alpha_2j = np.round((1 - data['other'].to_numpy()) * data.proportion.to_numpy() * participants)
print(alpha_2j)
alpha_1j = valores[:, 0] / (valores[:, 0] + valores[:, 1]) * data.proportion.to_numpy() * participants
print(alpha_1j)
new_values = np.round(np.stack([alpha_1j, alpha_2j], axis=1))
print(new_values)
With Stan:
model_hier="""
data {
int<lower=0> N;
int<lower=0> n;
int post[N, n];
}
parameters {
vector[n] mu;
cholesky_factor_corr[n] L;
simplex[n] alphas[N];
vector[n] beta[N];
}
transformed parameters{
vector[n] theta[N];
for (i in 1:N)
theta[i] = inv_logit(beta[i]);
}
model {
L ~ lkj_corr_cholesky(3.0);
mu ~ cauchy(0, 5);
beta ~ multi_normal_cholesky(mu, L);
for (i in 1:N)
alphas[i] ~ dirichlet(theta[i]);
for (i in 1:N)
post[i] ~ multinomial(alphas[i]);
}
generated quantities {
corr_matrix[n] Sigma;
Sigma = multiply_lower_tri_self_transpose(L);
}
"""
I have to say I am not happy about the code.
stan_model2 = pystan.StanModel(model_code=model_hier)
data3 = {'N': 16,
'n': 2,
'post': new_values.astype(int)}
fit2 = stan_model2.sampling(data=data3, algorithm='HMC', iter=4000, verbose=True)
Of course, there are warnings:
WARNING:pystan:n_eff / iter below 0.001 indicates that the effective sample size has likely been overestimated
WARNING:pystan:Rhat above 1.1 or below 0.9 indicates that the chains very likely have not mixed
WARNING:pystan:Skipping check of divergent transitions (divergence)
WARNING:pystan:Skipping check of transitions ending prematurely due to maximum tree depth limit (treedepth)
The output is very long
print(fit2.stansummary(digits_summary=5))
Inference for Stan model: anon_model_958bb8552d6652a8814e6044bd42f4a8.
4 chains, each with iter=4000; warmup=2000; thin=1;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu[1] 2.2705e1 8.01884.6381e1 1.1962 3.6407 7.20241.7178e11.7396e2 33 1.1352
mu[2] 2.0993e1 4.87353.433e1 2.2160 4.9229 8.72791.931e11.4692e2 50 1.0651
L[1,1] 1.0 nan 0.0 1.0 1.0 1.0 1.0 1.0 nan nan
L[2,1] -0.000 0.0056 0.3769 -0.709 -0.275 0.0006 0.2848 0.7012 4423 0.9999
L[1,2] 0.0 nan 0.0 0.0 0.0 0.0 0.0 0.0 nan nan
L[2,2] 0.9210 0.0023 0.0976 0.6453 0.8878 0.9600 0.9904 0.9999 1741 1.0020
alphas[1,1] 0.2707 0.0002 0.0572 0.1649 0.2311 0.2686 0.3065 0.3915 39793 0.9996
alphas[2,1] 0.352 0.0006 0.0556 0.2468 0.3122 0.3519 0.3904 0.4620 8197 0.9998
alphas[3,1] 0.3770 0.0001 0.0308 0.3166 0.3565 0.3769 0.3975 0.4385 34281 0.9995
alphas[4,1] 0.3306 0.0005 0.0456 0.2474 0.2974 0.3295 0.3627 0.4174 7888 1.0011
alphas[5,1] 0.3426 0.0010 0.0577 0.2351 0.3024 0.3405 0.3821 0.4602 2831 1.0003
alphas[6,1] 0.3604 0.0002 0.0361 0.2878 0.3384 0.3600 0.3816 0.4350 19799 0.9995
alphas[7,1] 0.3890 0.0003 0.0362 0.3204 0.3638 0.3891 0.4134 0.4601 13714 0.9997
alphas[8,1] 0.4110 0.0005 0.0340 0.3451 0.3896 0.4106 0.4324 0.48 4225 1.0001
alphas[9,1] 0.4282 0.0004 0.0822 0.2730 0.3697 0.4263 0.4849 0.5934 33091 0.9995
alphas[10,1] 0.3791 0.0009 0.0393 0.3048 0.3516 0.3782 0.4053 0.4580 1595 1.0016
alphas[11,1] 0.3804 0.0003 0.0379 0.3069 0.3543 0.3802 0.4063 0.4566 9941 0.9996
alphas[12,1] 0.4053 0.0002 0.0291 0.3484 0.3852 0.4051 0.425 0.4637 22000 0.9997
alphas[13,1] 0.3529 0.0004 0.0701 0.2175 0.3060 0.3507 0.3983 0.4993 28748 0.9996
alphas[14,1] 0.4052 0.0002 0.0456 0.3173 0.3727 0.4055 0.4370 0.4955 33739 0.9995
alphas[15,1] 0.3970 0.0001 0.0325 0.3342 0.3747 0.3964 0.4189 0.4611 49240 0.9996
alphas[16,1] 0.3979 0.0004 0.0453 0.3108 0.3667 0.3974 0.4286 0.4883 11043 0.9997
alphas[1,2] 0.7292 0.0002 0.0572 0.6084 0.6934 0.7313 0.7688 0.8350 39793 0.9996
alphas[2,2] 0.648 0.0006 0.0556 0.5379 0.6095 0.6480 0.6877 0.7531 8197 0.9998
alphas[3,2] 0.6229 0.0001 0.0308 0.5614 0.6024 0.6230 0.6434 0.6833 34281 0.9995
alphas[4,2] 0.6693 0.0005 0.0456 0.5825 0.6372 0.6704 0.7025 0.7525 7888 1.0011
alphas[5,2] 0.6573 0.0010 0.0577 0.5397 0.6179 0.6594 0.6975 0.7648 2831 1.0003
alphas[6,2] 0.6395 0.0002 0.0361 0.5649 0.6183 0.6399 0.6615 0.7121 19799 0.9995
alphas[7,2] 0.6109 0.0003 0.0362 0.5398 0.5865 0.6108 0.6362 0.6796 13714 0.9997
alphas[8,2] 0.5889 0.0005 0.0340 0.52 0.5675 0.5893 0.6104 0.6548 4225 1.0001
alphas[9,2] 0.5717 0.0004 0.0822 0.4065 0.5150 0.5736 0.6302 0.7269 33091 0.9995
alphas[10,2] 0.6208 0.0009 0.0393 0.5419 0.5946 0.6217 0.6483 0.6951 1595 1.0016
alphas[11,2] 0.6195 0.0003 0.0379 0.5433 0.5937 0.6197 0.6456 0.6930 9941 0.9996
alphas[12,2] 0.5947 0.0002 0.0291 0.5362 0.575 0.5948 0.6147 0.6515 22000 0.9997
alphas[13,2] 0.6470 0.0004 0.0701 0.5006 0.6016 0.6493 0.6939 0.7824 28748 0.9996
alphas[14,2] 0.5948 0.0002 0.0456 0.5044 0.5629 0.5944 0.6272 0.6827 33739 0.9995
alphas[15,2] 0.6029 0.0001 0.0325 0.5388 0.5810 0.6035 0.6253 0.6657 49240 0.9996
alphas[16,2] 0.6020 0.0004 0.0453 0.5116 0.5713 0.6025 0.6333 0.6891 11043 0.9997
beta[1,1] 2.2713e1 8.01864.6367e1 0.7253 3.7020 7.29131.7041e11.7394e2 33 1.1354
beta[2,1] 2.2719e1 8.01924.6396e1 0.7869 3.6451 7.28721.7319e11.7264e2 33 1.1352
beta[3,1] 2.2694e1 8.02054.6386e1 0.7152 3.6263 7.24291.7117e11.7349e2 33 1.1352
beta[4,1] 2.2711e1 8.01274.6375e1 0.7990 3.7203 7.2744 1.72e11.7371e2 33 1.1350
beta[5,1] 2.2706e1 8.01994.6389e1 0.6911 3.6927 7.28541.7143e11.7308e2 33 1.1352
beta[6,1] 2.2696e1 8.01374.6386e1 0.7916 3.6592 7.29001.7171e11.7384e2 34 1.1350
beta[7,1] 2.2715e1 8.02274.6393e1 0.7666 3.7174 7.29451.7197e11.7365e2 33 1.1354
beta[8,1] 2.2714e1 8.01464.6374e1 0.7420 3.7158 7.28731.7187e11.7354e2 33 1.1352
beta[9,1] 2.2729e1 8.01774.6387e1 0.8191 3.6922 7.16941.7145e11.7301e2 33 1.1352
beta[10,1] 2.2718e1 8.01684.6386e1 0.8272 3.7168 7.22621.7146e11.744e2 33 1.1351
beta[11,1] 2.2725e1 8.01984.6402e1 0.8458 3.6746 7.2161.7197e11.7302e2 33 1.1351
beta[12,1] 2.2711e1 8.01864.638e1 0.6594 3.6695 7.27421.7207e11.7349e2 33 1.1352
beta[13,1] 2.2708e1 8.01604.637e1 0.6844 3.7449 7.25291.7199e11.7331e2 33 1.1352
beta[14,1] 2.2719e1 8.01824.6392e1 0.7666 3.6791 7.27351.7018e11.735e2 33 1.1352
beta[15,1] 2.2716e1 8.01634.6394e1 0.8257 3.6758 7.26291.7119e11.7331e2 33 1.1351
beta[16,1] 2.2715e1 8.01634.6387e1 0.7689 3.6845 7.22611.7126e11.731e2 33 1.1350
beta[1,2] 2.101e1 4.87323.4339e1 1.8136 4.9731 8.79371.943e11.4617e2 50 1.0649
beta[2,2] 2.1011e1 4.87093.4341e1 1.7563 5.0524 8.80251.9373e11.4657e2 50 1.0651
beta[3,2] 2.0995e1 4.87163.4329e1 1.6634 5.0308 8.7981.9455e11.4667e2 50 1.0649
beta[4,2] 2.1008e1 4.87323.4328e1 1.8091 5.0136 8.75131.9424e11.4693e2 50 1.0652
beta[5,2] 2.1034e1 4.86883.4318e1 1.8465 5.0907 8.73281.9448e11.4711e2 50 1.0650
beta[6,2] 2.1014e1 4.87743.4345e1 1.7678 5.0475 8.74091.9357e11.4671e2 50 1.0652
beta[7,2] 2.1019e1 4.87293.4342e1 1.8202 5.0471 8.77261.9426e11.4751e2 50 1.0650
beta[8,2] 2.1e1 4.87203.4343e1 1.7964 4.9918 8.78851.937e11.4724e2 50 1.0648
beta[9,2] 2.1003e1 4.87543.434e1 1.7889 4.9947 8.77091.9506e11.467e2 50 1.0651
beta[10,2] 2.1019e1 4.87453.4355e1 1.7801 5.0105 8.83531.9436e11.4755e2 50 1.0651
beta[11,2] 2.1011e1 4.88323.436e1 1.7745 4.9971 8.81831.9411e11.4697e2 50 1.0652
beta[12,2] 2.1e1 4.86893.4323e1 1.7969 5.0186 8.76581.9163e11.4668e2 50 1.0650
beta[13,2] 2.1024e1 4.86963.4322e1 1.7591 5.0657 8.77951.9546e11.4676e2 50 1.0645
beta[14,2] 2.1002e1 4.87323.4324e1 1.8039 4.9603 8.76831.9452e11.4686e2 50 1.0652
beta[15,2] 2.1013e1 4.87403.434e1 1.8079 4.9877 8.83411.9378e11.466e2 50 1.0654
beta[16,2] 2.1012e1 4.87293.4341e1 1.7040 5.0002 8.79891.9428e11.4713e2 50 1.0648
theta[1,1] 0.9628 0.0015 0.0904 0.6737 0.9759 0.9993 1.0 1.0 3549 1.0039
theta[2,1] 0.9627 0.0016 0.0897 0.6871 0.9745 0.9993 1.0 1.0 3053 1.0045
theta[3,1] 0.9631 0.0016 0.0900 0.6715 0.9740 0.9992 1.0 1.0 2994 1.0047
theta[4,1] 0.9642 0.0013 0.0869 0.6897 0.9763 0.9993 1.0 1.0 4015 1.0027
theta[5,1] 0.9629 0.0016 0.0884 0.6662 0.9757 0.9993 1.0 1.0 2989 1.0044
theta[6,1] 0.9628 0.0013 0.0896 0.6881 0.9749 0.9993 1.0 1.0 4184 1.0038
theta[7,1] 0.9633 0.0014 0.0885 0.6827 0.9762 0.9993 1.0 1.0 3702 1.0046
theta[8,1] 0.9629 0.0013 0.0904 0.6774 0.9762 0.9993 1.0 1.0 4262 1.0028
theta[9,1] 0.9652 0.0013 0.0832 0.6940 0.9756 0.9992 1.0 1.0 3682 1.0043
theta[10,1] 0.9645 0.0014 0.0858 0.6957 0.9762 0.9992 1.0 1.0 3582 1.0043
theta[11,1] 0.9650 0.0012 0.0827 0.6997 0.9752 0.9992 1.0 1.0 4558 1.0042
theta[12,1] 0.9627 0.0015 0.0897 0.6591 0.9751 0.9993 1.0 1.0 3395 1.0047
theta[13,1] 0.9627 0.0014 0.0899 0.6647 0.9769 0.9992 1.0 1.0 3858 1.0052
theta[14,1] 0.9632 0.0013 0.0893 0.6827 0.9753 0.9993 1.0 1.0 4132 1.0028
theta[15,1] 0.9643 0.0013 0.0858 0.6954 0.9753 0.9993 1.0 1.0 3811 1.0041
theta[16,1] 0.9638 0.0015 0.0868 0.6833 0.9755 0.9992 1.0 1.0 3231 1.0035
theta[1,2] 0.9855 0.0006 0.0429 0.8598 0.9931 0.9998 1.0 1.0 4995 1.0018
theta[2,2] 0.9848 0.0007 0.0458 0.8527 0.9936 0.9998 1.0 1.0 4314 1.0017
theta[3,2] 0.9846 0.0007 0.0454 0.8407 0.9935 0.9998 1.0 1.0 3969 1.0011
theta[4,2] 0.985 0.0006 0.0472 0.8592 0.9934 0.9998 1.0 1.0 5750 1.0013
theta[5,2] 0.9852 0.0007 0.0464 0.8637 0.9938 0.9998 1.0 1.0 4179 1.0008
theta[6,2] 0.9850 0.0006 0.0466 0.8541 0.9936 0.9998 1.0 1.0 5104 1.0019
theta[7,2] 0.9856 0.0006 0.0434 0.8606 0.9936 0.9998 1.0 1.0 4667 1.0007
theta[8,2] 0.9851 0.0006 0.0454 0.8577 0.9932 0.9998 1.0 1.0 4716 1.0008
theta[9,2] 0.9848 0.0006 0.0482 0.8567 0.9932 0.9998 1.0 1.0 5013 1.0013
theta[10,2] 0.9848 0.0006 0.0474 0.8557 0.9933 0.9998 1.0 1.0 5051 1.0013
theta[11,2] 0.9853 0.0006 0.0439 0.8550 0.9932 0.9998 1.0 1.0 4887 1.0009
theta[12,2] 0.9851 0.0006 0.0463 0.8577 0.9934 0.9998 1.0 1.0 5339 1.0006
theta[13,2] 0.9851 0.0006 0.0453 0.8531 0.9937 0.9998 1.0 1.0 5175 1.0003
theta[14,2] 0.9855 0.0006 0.0441 0.8586 0.9930 0.9998 1.0 1.0 4960 1.0016
theta[15,2] 0.9851 0.0006 0.0450 0.8591 0.9932 0.9998 1.0 1.0 4773 1.0011
theta[16,2] 0.9848 0.0007 0.0466 0.8460 0.9933 0.9998 1.0 1.0 4484 1.0013
Sigma[1,1] 1.0 nan 0.0 1.0 1.0 1.0 1.0 1.0 nan nan
Sigma[2,1] -0.000 0.0056 0.3769 -0.709 -0.275 0.0006 0.2848 0.7012 4423 0.9999
Sigma[1,2] -0.000 0.0056 0.3769 -0.709 -0.275 0.0006 0.2848 0.7012 4423 0.9999
Sigma[2,2] 1.01.0388e-188.708e-17 1.0 1.0 1.0 1.0 1.0 7027 0.9995
lp__ -1.4472e3 0.2517 5.6630-1.4594e3-1.4508e3-1.4469e3-1.4434e3-1.437e3 506 1.0095
Samples were drawn using HMC at Tue Jul 30 20:01:26 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
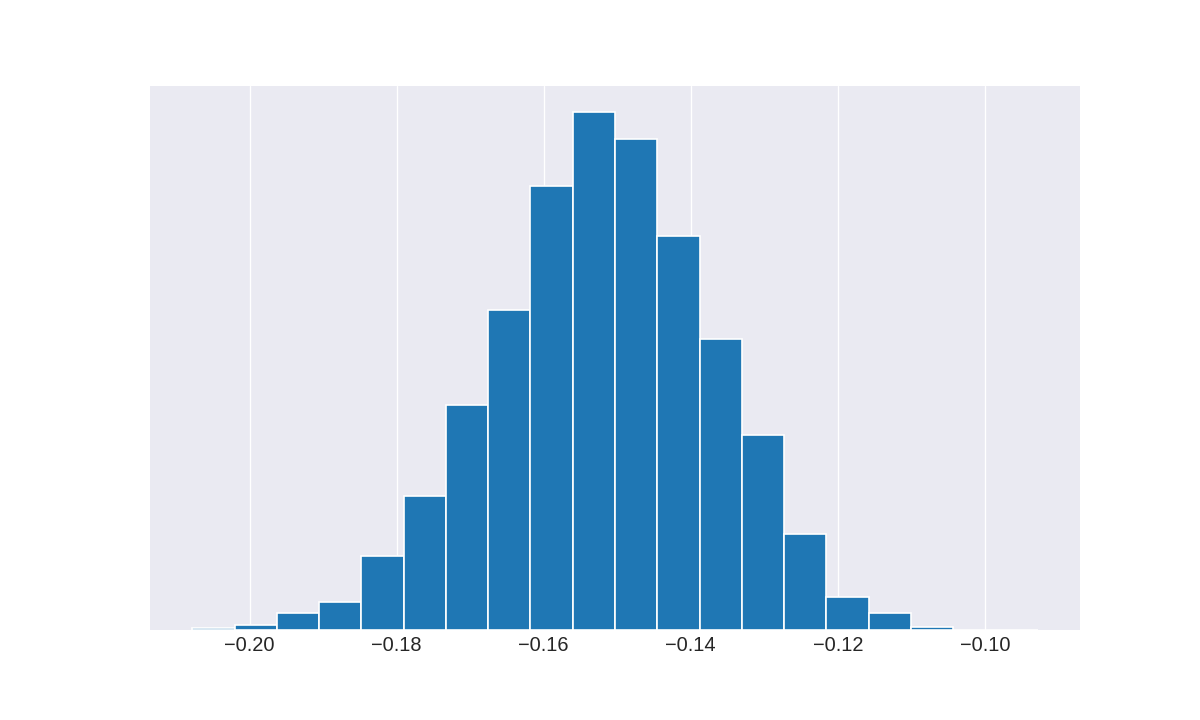
Let’s reproduce Figure 8.1(b)
samples2 = fit2.extract(permuted=True)['alphas']
th5 = []
for i in range(16):
result5 = 2 * samples2[:, i, 0] * samples2[:, i, 1] - samples2[:, i, 1]
th5.append(list(result5))
th5 = np.asarray(th5)
print(th5.shape)
res5 = np.sum(th5.T * proportion / np.sum(proportion), axis=1)
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(res5 , bins=20, edgecolor='w', density=True)
plt.show()
Do you know why that is weird?
The correct figure is (I think):
I have only changed the sign of res5. My Stan code could be wrong… but when you get the same figure with pymc3, you begin to doubt. The goal is then to improve the model (the diagnostics are not good), and that will be very hard.