Hi all,
—I am trying to fit a Bayesian hierarchical reinforcement learning model to my behavioral data. But I encountered three model fitting problems: divergent transitions , large R-hat values , and extremely low effective samples size . I failed to solve them after the following attempts and hereby seeking for some help. Let me walk through my study design first.
—( Study design ) Put simply, in my experiment participants ran a reinforcement learning go/no-go task. There are 4 within-subjects conditions (i.e., ‘goToWin’, ‘goToAvoid’, ‘nogoToWin’, ‘nogoToAvoid’), with 60 trials per condition, meaning that 240 trials per subject. Besides, each condition contains only one image, and images differ among these four training conditions. I have 72 subjects in total.
—( Model fitting ) Following is my reinforcement learning model with a hierarchical structure at the subject-level. In total, I have 20 hyper parameters, and note that I already employed both vectorization and non-centered parameterization in my Stan code. I fitted this model using 4 chains , with 2000 warm-up and 5000 iterations per chain.
data {
// number of subjects
int<lower=1> N;
// number of trials (i.e., 240 trials per subject)
int<lower=1>T;
// cue per trial for each subject: 1 = goToWin; 2 = goToAvoid; 3 = nogoToWin; 4 = nogoToAvoid
int<lower=1, upper=4> cue[N, T];
// action per trial for each subject: 0 = nogo and 1 = go
int<lower=0, upper=1> action[N, T];
// action per trial for each subject: -1 = loss, 0 = nothing/neutral, 1 = reward
real outcome[N, T];
}
transformed data {
vector[4] initV;
initV = rep_vector(0.0, 4);
}
parameters {
// in total we have ten parameters of interest:
// 1) xi
// 2) ep
// 3) b
// 4) pi
// 5) rhoRew
// 6) rhoPun
// 7) alpha_goToWin
// 8) alpha_goToAvoid
// 9) alpha_nogoToWin
// 10) alpha_nogoToAvoid
// 'mu_pr' contains ten aforementioned parameters at the population-level.
vector[10] mu_pr;
// 'sigma' contains ten variances/deviations correspond to the aforementioned ten population-level parameterss
vector<lower=0>[10] sigma;
vector[N] xi_pr; // each element follows a standard normal distribution
vector[N] ep_pr;
vector[N] b_pr;
vector[N] pi_pr;
vector[N] rhoRew_pr;
vector[N] rhoPun_pr;
vector[N] alpha_goToWin_pr;
vector[N] alpha_goToAvoid_pr;
vector[N] alpha_nogoToWin_pr;
vector[N] alpha_nogoToAvoid_pr;
}
transformed parameters{
vector<lower=0, upper=1>[N] xi; // bounded between [0, 1]
vector<lower=0, upper=1>[N] ep; // bounded between [0, 1]
vector[N] b; // unbounded, namely (-Inf, Inf)
vector[N] pi; // unbounded, namely (-Inf, Inf)
vector<lower=0>[N] rhoRew; // bounded as [0, Inf)
vector<lower=0>[N] rhoPun; // bounded as [0, Inf)
vector<lower=-1, upper=1>[N] alpha_goToWin; // bounded between [-1, 1]
vector<lower=-1, upper=1>[N] alpha_goToAvoid; // bounded between [-1, 1]
vector<lower=-1, upper=1>[N] alpha_nogoToWin; // bounded between [-1, 1]
vector<lower=-1, upper=1>[N] alpha_nogoToAvoid; // bounded between [-1, 1]
// vectorization and non-centered parameterization
xi = Phi_approx(mu_pr[1] + sigma[1] * xi_pr);
ep = Phi_approx(mu_pr[2] + sigma[2] * ep_pr);
b = mu_pr[3] + sigma[3] * b_pr;
pi = mu_pr[4] + sigma[4] * pi_pr;
rhoRew = exp(mu_pr[5] + sigma[5] * rhoRew_pr);
rhoPun = exp(mu_pr[6] + sigma[6] * rhoPun_pr);
alpha_goToWin = Phi_approx(mu_pr[7] + sigma[7] * alpha_goToWin_pr) * 2 - 1;
alpha_goToAvoid = Phi_approx(mu_pr[8] + sigma[8] * alpha_goToAvoid_pr) * 2 - 1;
alpha_nogoToWin = Phi_approx(mu_pr[9] + sigma[9] * alpha_nogoToWin_pr) * 2 - 1;
alpha_nogoToAvoid = Phi_approx(mu_pr[10] + sigma[10] * alpha_nogoToAvoid_pr) * 2 - 1;
}
model {
// define the priors for those hyper parameters
mu_pr[1] ~ normal(0, 1.0); // xi
mu_pr[2] ~ normal(0, 1.0); // ep
mu_pr[3] ~ normal(0, 10.0); // b
mu_pr[4] ~ normal(0, 10.0); // pi
mu_pr[5] ~ normal(0, 1.0); // rhoRew
mu_pr[6] ~ normal(0, 1.0); // rhoPun
mu_pr[7] ~ normal(0, 1.0); // alpha_goToWin
mu_pr[8] ~ normal(0, 1.0); // alpha_goToAvoid
mu_pr[9] ~ normal(0, 1.0); // alpha_nogoToWin
mu_pr[10] ~ normal(0, 1.0); // alpha_nogoToAvoid
sigma[1] ~ normal(0, 0.2); // xi
sigma[2] ~ normal(0, 0.2); // ep
sigma[3] ~ cauchy(0, 1.0); // b
sigma[4] ~ cauchy(0, 1.0); // Pavlovian bias
sigma[5] ~ normal(0, 0.2); // rhoRew
sigma[6] ~ normal(0, 0.2); // rhoPun
sigma[7] ~ normal(0, 0.2); // alpha_goToWin
sigma[8] ~ normal(0, 0.2); // alpha_goToAvoid
sigma[9] ~ normal(0, 0.2); // alpha_nogoToWin
sigma[10] ~ normal(0, 0.2); // alpha_nogoToAvoid
// define the priors for those individual parameters (i.e., Matt trick)
xi_pr ~ normal(0, 1.0);
ep_pr ~ normal(0, 1.0);
b_pr ~ normal(0, 1.0);
pi_pr ~ normal(0, 1.0);
rhoRew_pr ~ normal(0, 1.0);
rhoPun_pr ~ normal(0, 1.0);
alpha_goToWin_pr ~ normal(0, 1.0);
alpha_goToAvoid_pr ~ normal(0, 1.0);
alpha_nogoToWin_pr ~ normal(0, 1.0);
alpha_nogoToAvoid_pr ~ normal(0, 1.0);
for (s in 1:N) {
vector[4] actionWeight_go;
vector[4] actionWeight_nogo;
vector[4] qValue_go;
vector[4] qValue_nogo;
vector[4] sv;
vector[4] pGo;
actionWeight_go = initV;
actionWeight_nogo = initV;
qValue_go = initV;
qValue_nogo = initV;
sv[1] = alpha_goToWin[s];
sv[2] = alpha_goToAvoid[s];
sv[3] = alpha_nogoToWin[s];
sv[4] = alpha_nogoToAvoid[s];
for (t in 1:T) {
actionWeight_go[cue[s, t]] = qValue_go[cue[s, t]] + b[s] + pi[s] * sv[cue[s, t]];
actionWeight_nogo[cue[s, t]] = qValue_nogo[cue[s, t]];
pGo[cue[s,t]] = inv_logit(actionWeight_go[cue[s, t]] - actionWeight_nogo[cue[s,t]]);
{
pGo[cue[s, t]] *= (1 - xi[s]);
pGo[cue[s, t]] += (xi[s]/2);
}
// Likelihood function
action[s, t] ~ bernoulli(pGo[cue[s, t]]);
// update the stimulus Pavlovian value (per condition)
if (outcome[s, t] >= 0) {
sv[cue[s, t]] += ep[s] * (rhoRew[s] * outcome[s, t] - sv[cue[s, t]]);
} else {
sv[cue[s, t]] += ep[s] * (rhoPun[s] * outcome[s, t] - sv[cue[s, t]]);
}
// update the action values
if (action[s, t] == 1) {
if (outcome[s, t] >= 0) {
qValue_go[cue[s, t]] += ep[s] * (rhoRew[s] * outcome[s, t] - qValue_go[cue[s, t]]);
} else {
qValue_go[cue[s, t]] += ep[s] * (rhoPun[s] * outcome[s, t] - qValue_go[cue[s, t]]);
}
} else {
if (outcome[s, t] >= 0) {
qValue_nogo[cue[s, t]] += ep[s] * (rhoRew[s] *outcome[s, t] - qValue_nogo[cue[s, t]]);
} else {
qValue_nogo[cue[s, t]] += ep[s] * (rhoPun[s] *outcome[s, t] - qValue_nogo[cue[s, t]]);
}
}
} // end of the loop for the trial-level
} // end of the loop for the subject-level
}
generated quantities {
// In this block we will calculate the log-likelihood for each subject
// re-declare the aforementioned ten population-level parameters
real<lower=0, upper=1> mu_xi;
real<lower=0, upper=1> mu_ep;
real mu_b;
real mu_pi;
real<lower=0> mu_rhoRew;
real<lower=0> mu_rhoPun;
real<lower=-1, upper=1> mu_alpha_goToWin;
real<lower=-1, upper=1> mu_alpha_goToAvoid;
real<lower=-1, upper=1> mu_alpha_nogoToWin;
real<lower=-1, upper=1> mu_alpha_nogoToAvoid;
// declare the log-likelihood
real log_lik[N];
mu_xi = Phi_approx(mu_pr[1]);
mu_ep = Phi_approx(mu_pr[2]);
mu_b = mu_pr[3];
mu_pi = mu_pr[4];
mu_rhoRew = exp(mu_pr[5]);
mu_rhoPun = exp(mu_pr[6]);
mu_alpha_goToWin = Phi_approx(mu_pr[7]) * 2 - 1;
mu_alpha_goToAvoid = Phi_approx(mu_pr[8]) * 2 - 1;
mu_alpha_nogoToWin = Phi_approx(mu_pr[9]) * 2 - 1;
mu_alpha_nogoToAvoid = Phi_approx(mu_pr[10]) * 2 - 1;
{ // local section, this saves time and space
for (s in 1:N) {
vector[4] actionWeight_go;
vector[4] actionWeight_nogo;
vector[4] qValue_go;
vector[4] qValue_nogo;
vector[4] sv;
vector[4] pGo;
actionWeight_go = initV;
actionWeight_nogo = initV;
qValue_go = initV;
qValue_nogo = initV;
sv[1] = alpha_goToWin[s];
sv[2] = alpha_goToAvoid[s];
sv[3] = alpha_nogoToWin[s];
sv[4] = alpha_nogoToAvoid[s];
log_lik[s] = 0;
for (t in 1:T) {
actionWeight_go[cue[s, t]] = qValue_go[cue[s, t]] + b[s] + pi[s] * sv[cue[s, t]];
actionWeight_nogo[cue[s, t]] = qValue_nogo[cue[s, t]];
pGo[cue[s,t]] = inv_logit(actionWeight_go[cue[s, t]] - actionWeight_nogo[cue[s,t]]);
{
pGo[cue[s, t]] *= (1 - xi[s]);
pGo[cue[s, t]] += (xi[s]/2);
}
// log-likelihood
log_lik[s] += bernoulli_lpmf(action[s, t] | pGo[cue[s, t]]);
// update the stimulus Pavlovian value
if (outcome[s, t] >= 0) {
sv[cue[s, t]] += ep[s] * (rhoRew[s] * outcome[s, t] - sv[cue[s, t]]);
} else {
sv[cue[s, t]] += ep[s] * (rhoPun[s] * outcome[s, t] - sv[cue[s, t]]);
}
// update the action values
if (action[s, t] == 1) {
if (outcome[s, t] >= 0) {
qValue_go[cue[s, t]] += ep[s] * (rhoRew[s] * outcome[s, t] - qValue_go[cue[s, t]]);
} else {
qValue_go[cue[s, t]] += ep[s] * (rhoPun[s] * outcome[s, t] - qValue_go[cue[s, t]]);
}
} else {
if (outcome[s, t] >= 0) {
qValue_nogo[cue[s, t]] += ep[s] * (rhoRew[s] *outcome[s, t] - qValue_nogo[cue[s, t]]);
} else {
qValue_nogo[cue[s, t]] += ep[s] * (rhoPun[s] *outcome[s, t] - qValue_nogo[cue[s, t]]);
}
}
} // end of the loop for the trial-level
} // end of the loop for the subject-level
}
}
—( Warning messages ) However, I encountered the following model fitting problems: divergent transitions, large R-hat values, and extremely low effective samples size.
—( R-hat values and n_eff for all hyper parameters )
—( traceplot for all hyper parameters )
—( trankplot for all hyper parameters )
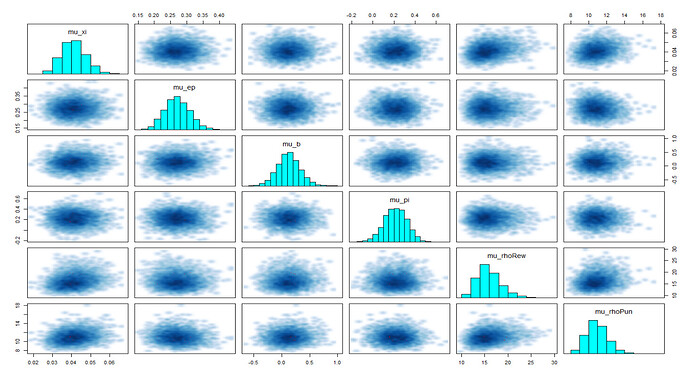
—( ‘pairs()’ to visualize all divergent transitions )
—( Model re-fitting and warning messages again ) Then, I re-fitted the same model using only 1 chain , with 1000 warm-up and 9000 iterations , besides, I also increased the ‘adapt_delta’ parameter to 0.99 . Once again, I got the following fitting problems:
—( R-hat values and n_eff for all hyper parameters )

—( traceplot for all hyper parameters )
—( ‘pairs()’ to visualize all divergent transitions )
—( Model re-re-fitting and warning messages again ) Finally, I re-refitted the same model using 8 chains , with 2,000 warm-up and 12,000 iterations , besides, I also increased the ‘adapt-delta’ parameter to 0.99 . But this time the situation became even worse.
—( traceplot and trank plot for all hyper parameters )
—( ‘pairs()’ to visualize all divergent transitions )
Does anyone see any clues in the aforementioned plots that I have missed? Or any other errors I’ve missed here, or have any thoughts about what might be going on here? I am worried that I am losing my mind and have set up the hierarchy wrong (i.e., perhaps model misspecification?) and just can’t see it. I would like to thank you and thank for any patience in advance.