I am looking forward to seeing what happens. Please be aware that this is not a validated approach and we actually need to do research to better understand the implications, but it looks promising at I think.
As @AlejandroCatalina explained previously, I am aware of the limitations of this method For the work I have to do it does not have to be bulletproof from a theoretical point of view. Nonetheless, I’m here to help, and I would be happy if this could open an “approximate” path that could help those who, in the community, face a problem similar to mine.
The solution @avehtari proposes would be interesting to try and should give at least an approximate idea for the selection of the variables. So it indeed looks interesting!
So @avehtari, @paul.buerkner, @AlejandroCatalina … I took some time to play with the model and I will split all the workflow in multiple posts.
The following two models are the Stan code that I used to generate a reproducible dataset (generate_data.stan) and to make inference about the parameters (ordinal_regression.stan).
I wrote the “generative code” looting Michael Betancourt’s code (so, thanks @betanalpha ! )
generate_data.stan generate_data.stan (976 Bytes) :
data {
int<lower = 0> N; // number of observation
int<lower = 0> M; // number of predictors
int<lower = 1> K; // number of ordinal categories
vector[K-1] c; // cut points
}
transformed data {
real<lower = 0, upper = 1> sig_prob = 0.05;
}
generated quantities {
vector[M] beta; // slopes
matrix[N, M] X; // predictors
vector[N] mu;
int y[N];
for (m in 1:M) {
if (bernoulli_rng(sig_prob)) {
if (bernoulli_rng(0.5)) {
beta[m] = normal_rng(10, 1);
} else {
beta[m] = normal_rng(-10, 1);
}
} else {
beta[m] = normal_rng(0, 0.25);
}
}
for (n in 1:N) {
for (m in 1:M) {
X[n, m] = normal_rng(0, 1); // all predictors are mean centered at 0 and standardized at 1
}
}
mu = X * beta;
for (n in 1:N) {
y[n] = ordered_logistic_rng(mu[n], c);
}
}
and ordinal_regression.stan ordinal_regression.stan (502 Bytes)
data {
int<lower = 0> N; // number of observation
int<lower = 0> M; // number of predictors
int<lower = 1> K; // number of ordinal categories
int<lower=1, upper=K> y[N]; // Observed ordinals
matrix[N, M] X; // predictors
}
parameters {
vector[M] beta; // slopes
ordered[K-1] c; // cut points
}
transformed parameters {
vector[N] mu = X * beta;
}
model {
c ~ student_t(3, 0, 2.5);
y ~ ordered_logistic(mu, c);
}
Then, with the following code I got slopes 30 slopes (relevant and irrelevant), 500 ordinal score son a 5-value scale, the predictor matrix, and I let stan do the inference.
remove(list = ls())
options(mc.cores = parallel::detectCores())
set.seed(123)
library(rstan)
rstan_options(auto_write = TRUE)
library(projpred)
N = 500 # number of observations
M = 30 # number of predictors
K = 5 # number of ordinal categories
c = sort(runif(n = K - 1, min = -5, max = 5))
generative = stan_model("./generate_data.stan")
gen = sampling(generative, data = list(N = N, M = M, K = K, c = c), seed = 123, algorithm = "Fixed_param", iter = 1, chains = 1)
beta = as.numeric(extract(gen, pars = "beta")$beta)
X = matrix(data = as.numeric(extract(gen, pars = "X")$X), nrow = N, ncol = M)
y = as.integer(extract(gen, pars = "y")$y)
model = stan_model("./ordinal_regression.stan")
fit = sampling(model, data = list(N = N, M = M, K = K, X = X, y = y), seed = 123, chains = 4)
mu = extract(fit, pars = "mu")
Emu = colMeans(mu$mu)
beta_out = extract(fit, pars = "beta")
beta_out = colMeans(beta_out$beta)
the “true” \beta are the following:
beta
[1] -0.233045611 -0.082993293 0.085635290 -0.135351220 -0.469997342
[6] 9.353118990 0.412084392 0.062155729 0.128925395 0.037598942
[11] 0.301502594 0.002788009 -0.075224657 -0.143522047 0.123930052
[16] 0.288065551 0.029104101 -0.023312894 -0.040097277 -0.174772110
[21] 9.476527099 0.008296223 -0.297025240 -0.221369662 -0.020534234
[26] 8.771793267 -12.259626932 0.456705693 0.185068152 -0.180819679
so, we should infer 4 relevant slopes (-12.259626932, 8.771793267, 9.353118990 , 9.476527099).
The followings are the modelled \beta:
eta_out
[1] -0.40676485 0.28088248 -0.07927991 -0.09320171 -0.80894627
[6] 16.42724226 1.48307589 0.45670540 -0.39804118 0.39808276
[11] 0.74836613 0.24019307 0.30879249 -0.20156108 0.23619630
[16] 0.62722394 0.17567108 -0.24024768 0.02899408 -0.32040050
[21] 17.71848729 0.03945813 -0.32671575 0.17693676 0.00956709
[26] 15.72181533 -21.54576394 0.03640765 0.66576612 -0.59754649
So, \beta are not very precise, neither the cut-points c are. However the relevant slopes are still relevant after the inference. Maybe better priors helps…
Now, with the posterior predictive distribution, the reference model can be set.
The following step is to set the reference model, in the way suggested by @avehtari.
mu = extract(fit, pars = "mu")
Emu = colMeans(mu$mu)
beta_out = extract(fit, pars = "beta")
beta_out = colMeans(beta_out$beta)
predfun = function(xt) t( beta %*% t(xt) )
sigma = rep(1.6, 4000)
ref = init_refmodel(X, Emu, gaussian(), x = X, predfun = predfun, dis = sigma)
To define the \sigma vector I set the nuber of iterations to 4000 (warmup+sampling), and as far as I understood the predictive projection, I used two times the predictor matrix X (one is the argumento of the predfun function) because I should project the X against the predicted \mu.
vs = varsel(ref, method = 'forward') finds 4 relevant \beta :
and the relevant sole are correctly identified:
selected = as.integer(vs$vind)[1:4]
beta_fitted = beta_out[selected]
[1] -21.54576 17.71849 16.42724 15.72182
So, the approximation works. However some useful commands do not work: for example:
suggest_size(vs)
[1] NA
Warning message:
In suggest_size(vs) :
Could not suggest model size. Investigate varsel_plot to identify if the search was terminated too early. If this is the case, run variable selection with larger value for nv_max.
suggest_size(vs, stat = "rmse") works and identifies 6 relevant slopes. cv_varsel(vs) does not work either:
Error in importance_sampling_object(unnormalized_log_weights = log_weights, :
is.matrix(unnormalized_log_weights) is not TRUE
In addition: Warning message:
Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.
I got so far, so now I would like to hear comment from your side. Thanks to guiding me through all this!
Cool!
Suggest size defaults to epld, and probably fails as the uncertainties in elpd differences are very small and difference goes to zero only with all variables. This might be related to fixing sigma. Alternative would be to estimate the sigma, too, which you can do by computing residual sigma for each beta and simulated data.
That seems like a bug. Do the projpred quickstart examples https://mc-stan.org/projpred/articles/quickstart.html work for you?
Thank you @fabio ! What is strange here that the ELPD decreases (becomes worse) when adding more predictors and has a quite weird scale. There may be something wrong here but I am not sure where. For me being able to replicate your experiments, could you tell me which version of projpred you used?
I also thought it was strange, but didn’t think much as it can’t be correct anyway as y is replaced with mu and sigma is fixed to 1.6. So currently you shouldn’t look at the elpd and it being wrong doesn’t affect the projection. RMSE is less sensitive to these issues. Of course if this latent space projpred seems to be useful, we should improve these functions and documentation.
If you have time it would be great if you repeat your experiment using the new refactored projpred version
devtools::install_github('stan-dev/projpred', ref="develop", build_vignettes = TRUE)
Especially interested if you get the same error with cv_varsel.
@paul.buerkner @avehtari: I will post something in the late evening.
@avehtari:, @pau the projpred quickstart example works:
I am using rstanarm_2.21.1 an projpred_1.1.6.
cvs_varsel() works, however, I get a warning:
Warning message:
Some Pareto k diagnostic values are slightly high. See help('pareto-k-diagnostic') for details.
but no error is raised. and the output of suggest_size() is 6 and not 7 as in the guide. I used iter = 550, chains =2, as in the guide. So @avehtari , if @paul.buerkner upgrades to the new projpred I could stick to my version and see what’s happening. Or just work on the development version… let me what you thinh it would be the best approach.
Great!
MCMC part has randomness which can show in suggested size, especially when using a small number of iterations. iter = 550 , chains =2 in the vignette wre used only to make the example quick, but they don’t reflect the recommended values.
You can use now what works. We hope to release the new projpred soon, so any additional testing will help, but no need to take the risk if you are worried about your time.
If I undersant correctly, the dis parameters is calculated as:
b_o = extract(fit, pars = "beta")
b_o = b_o$beta
sigma = apply(b_o,1, sd, na.rm = TRUE)
ref = init_refmodel(X, Emu, gaussian(), x = X, predfun = predfun, dis = sigma)
\sigma is far for being around 1.6, so maybe there is something “fishy” in my generative model:
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.089 6.053 6.583 6.624 7.149 10.485
and this is the graphical output of varsel_plot now:
RMSE still works better due to the approximation in the reference model. However, I’m here to help. I just start to grasp the concepts about projective variable selection, so keep in mind I could produce more entropy than results.
I will also try to run it myself later on this week. Thanks for testing @fabio!
If you need help by and end-user, I am here to help as a beta-tester.
The dispersion parameter sigma of the latent distribution is (implicitly) fixed for identification. Since you were using a latent logistic model, we know the latent SD is sqrt(pi^2/3) = 1.81 and people usually recommend something between 1.6 and that value. For comparison, if were had used a latent normal distribution, sigma would just be exactly 1.
so, souldn’t the scale parameter be calculated from X \beta? I calculated it just over \beta…
If we think of a linear Gaussian model (instead of an ordinal model), we have a parameter \sigma (sigma) which caputeres the residual standard deviation:
Clearly, \sigma cannot be computed just from the information in X \beta or \beta. In an ordinal model, \sigma is not identified as the ordinal responses lack scale information and so we (implictly) fix it for identification by used a latent distribution (normal or logistic) with fixed scale/dispersion.
For reference, I am now running this model with the new projpred. I will try to take a look into the ELPD as well to see what’s happening inside. Hopefully I’ll report something later on!
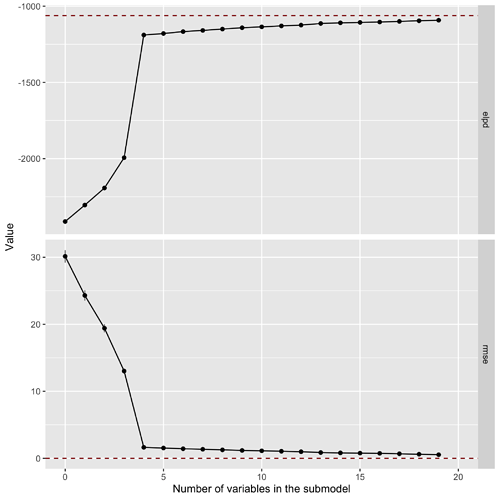
EDIT: I have now successfully run the model and this is the resulting variable selection plot:
It seems that the large number of data points make the standard error on the estimation quite small. Furthermore, because we are measuring the latent space, there seems to be some overfitting in place (RMSE of the reference model goes to 0).
I am now running cv_varsel to see if that outputs a more reasonable estimate. This is run on the latest projpred (in develop for now, yay!). The difference with @fabio’s results might be in sigma, which I took as the empirical standard deviation of mu.
The latest projpred requires some extra functions to be passed on to init_refmodel. We can probably turn this into a vignette (@avehtari and @paul.buerkner?) as this showcases yet another case of custom reference models.
EDIT2: If I now fix sigma to 1.6 for all draws I get this variable selection plot, which makes sense now as sigma is much smaller and fixed:
Running cv_varsel on the model with the empirical standard deviation returns basically the same result, with slightly corrected performances. In this case the standard deviation is probably too large. If we fix the dispersion to 1.6 the cross-validated variable selection looks like this:
which clearly indicates that the model is not very good (we already know that because we have the same fixed dispersion for all draws) while still roughly returning the same relevant variables (looking at RMSE).
That looks nice! I think it would be a good showcase for the vignette. Could you show the code you used for this example? I still wanted to play around with it as well but didn’t manage to do it yet…