Inquiries about variable selection using projpred

[kendyteng]

I am writing a paper that involves using projpred for covariate selection for my model, and I am hoping to get some help to get my analyses and their descriptions right.

I was constructing a Poisson BYM2 model for the risk of Salmonella infection at pig-farm level in Spain. I examined some covariates that were related to pig or farm numbers/types. During the variable selection process, the BYM2 component was not included in the model.

Like in the Quick Start vignette of prejpred, I used a regularised horseshoe prior to constructed my reference model, followed by the “cv_varsel” function as in the following code.

cv_varsel(M.pois.hs, method = 'forward', cv_method = 'loo')

The first question is that in the case of loo, how are the variables ranked for the forward process?

Here is how I wrote about the procedure. Could you please have a quick browse and see whether they are correctly done and stated?

The predictive projection technique proposed by (Piironen et al., 2018) was implemented for the covariate selection with ‘projpred’ package (Piironen et al., 2019). The selection process contained two steps. Firstly, a Bayesian penalised regression model with a regularised horseshoe prior and all the covariates was constructed as the reference model that warranted a good prediction ability. Secondly, a forward stepwise addition of covariates that increased the mean log predictive density the most in the leave-one-out cross-validation , starting from the intercept term, was performed. A minimal subset of these covariates in a model which had similar predictive power as the reference model, judged by the mean log predictive density, were to be included in the final model.

The other issue that I’ve encountered is that it seems that my covariates do not predict very well at all. Here is the graph from the following code.

print(varsel_plot(cvs, stats = c('elpd', 'rmse'), deltas = T))

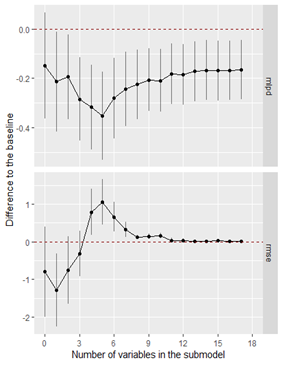
Eventually, I chose the first two covariates to be included in the model as in the regular projection (codes as below), the mlpd and mrse substantially improved after the inclusion of the second covariate.

vs <- varsel(M.pois.hs, method = "L1")
varsel_plot(vs, stats = c('elpd', 'mlpd'), deltas = T)

I wonder what are the comments on this scenario?

Thank you very much!
Cheers
Kendy

[torkar]

@kendyteng, the first plot is not visible to me?

[kendyteng]

Thank you @torkar! Can you see it now?

[torkar]

I think @avehtari is most likely the person to answer this!

[avehtari]

Thanks for moving the question here from email. I think this may be interesting also for others.

@kendyteng

M.pois.hs

Can you show how this is defined? It’s not necessary for answering your later questions, but helps to check if there might be other problems.

@kendyteng

Secondly, a forward stepwise addition of covariates that increased the mean log predictive density the most in the leave-one-out cross-validation , starting from the intercept term, was performed.

Secondly, a forward stepwise addition of covariates that decreased the Kullback-Leibler divergence from the reference model to the projected submodel. This stepwise addition finds the best model for each submodel size. A smallest submodel, having the minimal subset of these covariates which has similar predictive power as the reference model, judged by the mean log predictive density, is selected.

@kendyteng

The other issue that I’ve encountered is that it seems that my covariates do not predict very well at all.

Yes, these look bad. Can you post also plots with deltas = F? This would show also how bad the reference model is.

@kendyteng

Eventually, I chose the first two covariates to be included in the model as in the regular projection (codes as below)

I would say that cv_varsel is the regular one. varsel can be misleading in difficult cases.

[kendyteng]

Thank you very much, Aki!

@avehtari

Can you show how this is defined? It’s not necessary for answering your later questions, but helps to check if there might be other problems.

Yes, here it is.

f <- as.formula(paste("obs ~", 
                       paste(names(D.spldf.st)[9:31], collapse = "+"), 
                       "+offset(log(exp))"))
M.pois.hs <- brm(formula = f, data = D.spldf.st, 
                 family = poisson(), seed = 19871002,
                 set_prior(horseshoe(df = 1.5, par_ratio = 0.1)),
                 control = list(adapt_delta = 0.999999, max_treedepth = 12))

@avehtari

Yes, these look bad. Can you post also plots with deltas = F? This would show also how bad the reference model is.

Here are the graphs. I wonder how you judge how bad the reference model is?

@avehtari

I would say that cv_varsel is the regular one. varsel can be misleading in difficult cases.

Ok, I see. In this case, should I include any of the covariates? The covariates are actually from different data source. I don’t expect it to fit very well. The purpose is more to build a BYM2 model, but of course I was hoping that they could explain something.

[avehtari]

@kendyteng

Yes, here it is.

Where is the BYM part?

@kendyteng

set_prior(horseshoe(df = 1.5, par_ratio = 0.1)), control = list(adapt_delta = 0.999999,

Did you have problems with df=1, which would give more sparse results?

Did you have problems with smaller adapt_delta, as 0.999999 is very extreme?

@kendyteng

I wonder how you judge how bad the reference model is?

You can compare rmse to SD of target variable.

Also you could plot PPC plots with bayesplot to see more about how good your model is. I guess that you may have overdipersion compared to Poisson and negative binomial would be better.

@kendyteng

In this case, should I include any of the covariates?

Based on the current information yes. Let’s see PPC results and if negative binomial help at all.

[anon75146577]

Slightly orthogonal for the conversation but relevant: adding a bym2 component to the model can do surprising things to the covariates so even if you’re seeing “bad behaviour” it may still be correct https://www4.stat.ncsu.edu/~bjreich/papers/FixedEffectsYouLove.pdf

[kendyteng]

Thank you @anon75146577 for the paper! I’ve wondered about this for a while.

@avehtari
I did included the BYM part because I wasn’t able to project when I included it. I hope it was just I didn’t know how to do it so that I will be able to add the BYM term during the variable section.

@avehtari

Did you have problems with df=1, which would give more sparse results?
Did you have problems with smaller adapt_delta, as 0.999999 is very extreme?

I tried it again. Actually, adapt_delta = 0.99999 is enough, but I guess it’s still quite large?
When I specified df=1, it did give a bit more sparse results but the difference is quite small. I just attach the plots of df=1 here for comparison.

cvs1 <- cv_varsel(M.pois.hs1, method = 'forward', cv_method = 'loo')
print(varsel_plot(cvs1, stats = c('mlpd', 'rmse'), deltas = T))

print(varsel_plot(cvs1, stats = c('mlpd', 'rmse'), deltas = F))

@avehtari

Also you could plot PPC plots with bayesplot to see more about how good your model is. I guess that you may have overdipersion compared to Poisson and negative binomial would be better.

Here are some PCC plots of the Poisson model and negative-binomial and I compared them using loo. My workflow was to do the model selection with a Poisson model → add the BYM term → examine the fitness of the model with different family, including the negative-binomial model. Does this sound legit? Or it’s better I do it at this stage?

ppc_rootogram(Y, yrep = Ysim.pois.hs)

ppc_rootogram(Y, yrep = Ysim.negbi.hs)

#standardised residuals of the observed vs predicted number
Ysim.pois.hs_mean <- colMeans(Ysim.pois.hs) #column mean
F.pois.hs_std_resid <- (Y - Ysim.pois.hs_mean) / sqrt(Ysim.pois.hs_mean) 
qplot(Ysim.pois.hs_mean, F.pois.hs_std_resid, ylab = "Standardised residuals",
      xlab = "Mean of the predict responses based on the fitted model")+ 
   hline_at(2) + hline_at(-2)

Ysim.negbi.hs_mean <- colMeans(Ysim.negbi.hs) #column mean
F.negbi.hs_std_resid <- (Y - Ysim.negbi.hs_mean) / sqrt(Ysim.negbi.hs_mean) 
qplot(Ysim.negbi.hs_mean, F.negbi.hs_std_resid, ylab = "Standardised residuals",
     xlab = "Mean of the predict responses based on the fitted model")+ 
  hline_at(2) + hline_at(-2) 

And I also used loo to compare these two models, and I’ve got 3 and 8 observations with a pareto_k > 0.7 in model ‘M.negbi.hs’ and ‘M.pois.hs’, respectively. So I used reloo.
loo(M.negbi.hs, M.pois.hs, reloo = T)

Computed from 4000 by 43 log-likelihood matrix

         Estimate   SE
elpd_loo   -126.0  9.0
p_loo         4.5  2.5
looic       252.0 18.0
------
Monte Carlo SE of elpd_loo is 0.2.

Pareto k diagnostic values:
                         Count Pct.    Min. n_eff
(-Inf, 0.5]   (good)     38    88.4%   31        
 (0.5, 0.7]   (ok)        5    11.6%   1280      
   (0.7, 1]   (bad)       0     0.0%   <NA>      
   (1, Inf)   (very bad)  0     0.0%   <NA>      

All Pareto k estimates are ok (k < 0.7).
See help('pareto-k-diagnostic') for details.

Output of model 'M.pois.hs':

Computed from 4000 by 43 log-likelihood matrix

         Estimate   SE
elpd_loo   -137.6 15.4
p_loo        26.4 12.3
looic       275.1 30.9
------
Monte Carlo SE of elpd_loo is NA.

Pareto k diagnostic values:
                         Count Pct.    Min. n_eff
(-Inf, 0.5]   (good)     40    93.0%   1         
 (0.5, 0.7]   (ok)        3     7.0%   799       
   (0.7, 1]   (bad)       0     0.0%   <NA>      
   (1, Inf)   (very bad)  0     0.0%   <NA>      

All Pareto k estimates are ok (k < 0.7).
See help('pareto-k-diagnostic') for details.

Model comparisons:
           elpd_diff se_diff
M.negbi.hs   0.0       0.0  
M.pois.hs  -11.5       7.4

It appears that negative-binomial model fits better although the standardised residuals from the Poisson model seems to be better.

[avehtari]

@kendyteng

Actually, adapt_delta = 0.99999 is enough, but I guess it’s still quite large?

Yes.

@kendyteng

When I specified df=1, it did give a bit more sparse results but the difference is quite small.

That is expected with as there is not that many variables. I was just interested whether you had problems with df=1, as learning problematic cases helps us understand horseshoe better.

The difference between Poisson and negative binomial is small. There doesn’t seem to be useful information in covariates.

@kendyteng

My workflow was to do the model selection with a Poisson model → add the BYM term → examine the fitness of the model with different family, including the negative-binomial model.

I would do the model selection also with negative-binomial as it includes Poisson as a special case (given sensible prior on overdispersion parameter).

I think projpred doesn’t support yet BYM, so it is sensible to do the variable selection first. You might get different result if you could do the variable selection with BYM included (or other spatial model), but I think it’s likely that these covariates just don’t have much useful information.

[kendyteng]

@avehtari

@kendyteng

Actually, adapt_delta = 0.99999 is enough, but I guess it’s still quite large?

Yes.

But would that be other problem to use large adapt_delta apart from it taking longer?
Sometimes the output recommends me to use an adapt_delta above 1, but I thought the max is 1, or not?

@avehtari

That is expected with as there is not that many variables. I was just interested whether you had problems with df=1, as learning problematic cases helps us understand horseshoe better.

I am happy to share the data for you to explore if you think that would help.

[mcol]

@kendyteng

But would that be other problem to use large adapt_delta apart from it taking longer?

Such extreme values of adapt_delta are generally indications of bad geometry,s such as funnel-like regions that the sampler has troubles exploring unless the stepsize becomes really small. This can sometimes be remedied with alternative formulations or stronger priors.

[kendyteng]

Thank you @mcol :)
Many thanks to @avehtari. Really appreciate you help!