Hey @ucfagls, thank you for the helpful answer. I apologize for the response lag. After putting this on the shelf for a while, and with the help from Steve Wild, it’s now clear how to make this work with brms. For posterity, I’ll work it out in two ways:
The single-level option
You’re right to bring up the identifiability issue. Happily, even modest priors solve that problem within the Bayesian context.
Load the focal packages and the data.
library(tidyverse)
library(brms)
library(splines)
data(cherry_blossoms, package = "rethinking")
d <- cherry_blossoms
rm(cherry_blossoms)
# drop missing cases
d2 <-
d %>%
drop_na(doy)
Define the knots and the b-splines.
num_knots <- 15
knot_list <- quantile(d2$year, probs = seq(from = 0, to = 1, length.out = num_knots))
B <- bs(d2$year,
knots = knot_list[-c(1, num_knots)],
degree = 3,
intercept = TRUE)
Make a new data set which includes B as a matrix column.
d3 <-
d2 %>%
mutate(B = B)
Fit the model.
b4.8 <-
brm(data = d3,
family = gaussian,
doy ~ 1 + B,
prior = c(prior(normal(100, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(exponential(1), class = sigma)),
iter = 2000, warmup = 1000, chains = 4, cores = 4,
seed = 4)
Here’s the model summary.
print(b4.8)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: doy ~ 1 + B
Data: d3 (Number of observations: 827)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 103.59 2.49 98.58 108.45 1.01 761 1071
B1 -3.19 3.88 -10.80 4.21 1.00 1591 2435
B2 -1.11 3.92 -8.82 6.62 1.00 1463 1859
B3 -1.27 3.68 -8.58 6.07 1.00 1332 1833
B4 4.56 2.96 -1.13 10.54 1.00 1046 1648
B5 -1.08 2.99 -6.89 4.78 1.00 954 1399
B6 4.03 3.02 -1.86 10.07 1.00 1056 1515
B7 -5.55 2.91 -11.23 0.30 1.00 981 1672
B8 7.57 2.92 1.92 13.29 1.00 1005 1583
B9 -1.22 2.97 -6.90 4.58 1.01 1001 1458
B10 2.79 3.03 -3.17 9.02 1.00 1019 1527
B11 4.42 3.00 -1.49 10.27 1.00 1056 1846
B12 -0.37 2.99 -5.98 5.70 1.00 1013 1551
B13 5.28 2.99 -0.52 11.07 1.00 1024 1768
B14 0.46 3.09 -5.44 6.74 1.00 1036 1712
B15 -1.05 3.37 -7.77 5.59 1.00 1215 2147
B16 -7.25 3.44 -14.01 -0.49 1.00 1287 1936
B17 -7.88 3.26 -14.24 -1.29 1.00 1246 1824
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 5.94 0.14 5.67 6.23 1.00 4173 2921
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
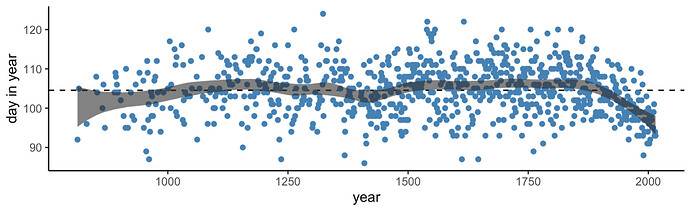
Make the bottom panel of McElreath’s Figure 4.13 (p. 118).
fitted(b4.8) %>%
data.frame() %>%
bind_cols(d3) %>%
ggplot(aes(x = year, y = doy, ymin = Q2.5, ymax = Q97.5)) +
geom_hline(yintercept = fixef(b4.8)[1, 1], linetype = 2) +
geom_point(color = "steelblue") +
geom_ribbon(alpha = 2/3) +
labs(x = "year",
y = "day in year") +
theme_classic()
The multilevel option
It seems like we can get a pretty close s()-based analogue with a little tweeking. Here’s my attempt.
b4.11 <-
brm(data = d2,
family = gaussian,
doy ~ 1 + s(year, bs = "bs", k = 19),
prior = c(prior(normal(100, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(student_t(3, 0, 5.9), class = sds),
prior(exponential(1), class = sigma)),
iter = 2000, warmup = 1000, chains = 4, cores = 4,
seed = 4,
control = list(adapt_delta = .99))
Parameter summary:
posterior_summary(b4.11)[-22, ] %>% round(2)
Estimate Est.Error Q2.5 Q97.5
b_Intercept 104.54 0.20 104.14 104.95
bs_syear_1 -0.09 0.33 -0.75 0.57
sds_syear_1 1.31 0.59 0.54 2.80
sigma 5.98 0.15 5.70 6.28
s_syear_1[1] -1.37 1.67 -5.50 1.02
s_syear_1[2] -0.38 0.10 -0.60 -0.19
s_syear_1[3] 0.40 0.24 -0.09 0.88
s_syear_1[4] 1.19 0.42 0.40 2.08
s_syear_1[5] 0.78 0.61 -0.43 2.04
s_syear_1[6] 0.11 0.78 -1.38 1.79
s_syear_1[7] 0.48 0.93 -1.36 2.39
s_syear_1[8] 0.33 1.01 -1.59 2.44
s_syear_1[9] 0.95 1.00 -0.96 3.09
s_syear_1[10] -0.80 0.95 -2.82 1.02
s_syear_1[11] -0.43 0.92 -2.38 1.33
s_syear_1[12] -0.20 0.93 -2.08 1.69
s_syear_1[13] 0.57 1.06 -1.33 2.88
s_syear_1[14] 1.04 1.21 -0.92 3.82
s_syear_1[15] -0.03 1.10 -2.33 2.20
s_syear_1[16] 1.47 1.46 -0.82 4.86
s_syear_1[17] 1.54 1.54 -0.77 5.38
Make the s()-based alternative to the bbottom panel of McElreath’s Figure 4.13.
fitted(b4.11) %>%
data.frame() %>%
bind_cols(d3) %>%
ggplot(aes(x = year, y = doy, ymin = Q2.5, ymax = Q97.5)) +
geom_hline(yintercept = fixef(b4.11)[1, 1], linetype = 2) +
geom_point(color = "steelblue") +
geom_ribbon(alpha = 2/3) +
labs(x = "year",
y = "day in year") +
theme_classic()
Here we might compare the bias weights from the two models with a coefficient plot.
bind_rows(
# single level
fixef(b4.8)[-1, -2] %>%
data.frame() %>%
mutate(number = 1:n(),
fit = "single level") %>%
select(fit, number, everything()),
# multilevel (with `s()`)
posterior_samples(b4.11) %>%
select(bs_syear_1, contains("[")) %>%
pivot_longer(-bs_syear_1, names_to = "number") %>%
mutate(bias = bs_syear_1 + value,
number = str_remove(number, "s_syear_1") %>% str_extract(., "\\d+") %>% as.integer()) %>%
group_by(number) %>%
summarise(Estimate = mean(bias),
Q2.5 = quantile(bias, probs = 0.025),
Q97.5 = quantile(bias, probs = 0.975)) %>%
mutate(fit = "multilevel") %>%
select(fit, number, everything())
) %>%
mutate(number = if_else(fit == "multilevel", number + 0.1, number - 0.1)) %>%
# plot
ggplot(aes(x = Estimate, xmin = Q2.5, xmax = Q97.5, y = number, color = fit)) +
geom_pointrange(fatten = 1) +
scale_color_viridis_d(option = "A", end = 2/3, direction = -1) +
theme_classic()
I’ll be uploading a more detailed walk-out of this workflow in my ebook, soon. In the meantime, the updated code lives on GitHub.