I have used brms to generate Stan code for a zero inflated Beta regression with interval censoring. I then used the example code provided by Hans Van Calster in this feature request, to modify the way the model handles censoring.
I used that model on data of leaf damage (10491 observations, zero or interval censored: 0, (0, .05], (.05, .25] or (.25, 1), clustered by taxon and location).
Stan code
// generated with {brms} 2.22.8 **and modified**
functions {
real zero_inflated_beta_lpdf(real y, real mu, real phi, real zi) {
row_vector[2] shape = [mu * phi, (1 - mu) * phi];
if (y == 0) {
return bernoulli_lpmf(1 | zi);
} else {
return bernoulli_lpmf(0 | zi) +
beta_lpdf(y | shape[1], shape[2]);
}
}
}
data {
int<lower=1> N; // total number of observations
vector[N] Y; // response variable
///////////////////////////////////////////////////////////////////////////////////////
// censoring indicator: 0 = event, 1 = right, -1 = left, 2 = interval censored
array[N] int<lower=-1,upper=2> cens;
// right censor points for interval censoring
vector[N] rcens;
///////////////////////////////////////////////////////////////////////////////////////
int<lower=1> K; // number of population-level effects
matrix[N, K] X; // population-level design matrix
int<lower=1> Kc; // number of population-level effects after centering
int<lower=1> K_zi; // number of population-level effects
matrix[N, K_zi] X_zi; // population-level design matrix
int<lower=1> Kc_zi; // number of population-level effects after centering
// data for group-level effects of ID 1
int<lower=1> N_1; // number of grouping levels
int<lower=1> M_1; // number of coefficients per level
array[N] int<lower=1> J_1; // grouping indicator per observation
// group-level predictor values
vector[N] Z_1_1;
// data for group-level effects of ID 2
int<lower=1> N_2; // number of grouping levels
int<lower=1> M_2; // number of coefficients per level
array[N] int<lower=1> J_2; // grouping indicator per observation
// group-level predictor values
vector[N] Z_2_1;
// data for group-level effects of ID 3
int<lower=1> N_3; // number of grouping levels
int<lower=1> M_3; // number of coefficients per level
array[N] int<lower=1> J_3; // grouping indicator per observation
// group-level predictor values
vector[N] Z_3_1;
// data for group-level effects of ID 4
int<lower=1> N_4; // number of grouping levels
int<lower=1> M_4; // number of coefficients per level
array[N] int<lower=1> J_4; // grouping indicator per observation
// group-level predictor values
vector[N] Z_4_zi_1;
// data for group-level effects of ID 5
int<lower=1> N_5; // number of grouping levels
int<lower=1> M_5; // number of coefficients per level
array[N] int<lower=1> J_5; // grouping indicator per observation
// group-level predictor values
vector[N] Z_5_zi_1;
// data for group-level effects of ID 6
int<lower=1> N_6; // number of grouping levels
int<lower=1> M_6; // number of coefficients per level
array[N] int<lower=1> J_6; // grouping indicator per observation
// group-level predictor values
vector[N] Z_6_zi_1;
int prior_only; // should the likelihood be ignored?
}
transformed data {
matrix[N, Kc] Xc; // centered version of X without an intercept
vector[Kc] means_X; // column means of X before centering
matrix[N, Kc_zi] Xc_zi; // centered version of X_zi without an intercept
vector[Kc_zi] means_X_zi; // column means of X_zi before centering
for (i in 2:K) {
means_X[i - 1] = mean(X[, i]);
Xc[, i - 1] = X[, i] - means_X[i - 1];
}
for (i in 2:K_zi) {
means_X_zi[i - 1] = mean(X_zi[, i]);
Xc_zi[, i - 1] = X_zi[, i] - means_X_zi[i - 1];
}
///////////////////////////////////////////////////////////////////////////////////////
// censoring indices
int Nevent = 0;
int Nrcens = 0;
int Nlcens = 0;
int Nicens = 0;
array[N] int Jevent;
array[N] int Jrcens;
array[N] int Jlcens;
array[N] int Jicens;
for (n in 1:N) {
if (cens[n] == 0) {
Nevent += 1;
Jevent[Nevent] = n;
} else if (cens[n] == 1) {
Nrcens += 1;
Jrcens[Nrcens] = n;
} else if (cens[n] == -1) {
Nlcens += 1;
Jlcens[Nlcens] = n;
} else if (cens[n] == 2) {
Nicens += 1;
Jicens[Nicens] = n;
}
}
///////////////////////////////////////////////////////////////////////////////////////
}
parameters {
vector[Kc] b; // regression coefficients
real Intercept; // temporary intercept for centered predictors
real<lower=0> phi; // precision parameter
vector[Kc_zi] b_zi; // regression coefficients
real Intercept_zi; // temporary intercept for centered predictors
vector<lower=0>[M_1] sd_1; // group-level standard deviations
array[M_1] vector[N_1] z_1; // standardized group-level effects
vector<lower=0>[M_2] sd_2; // group-level standard deviations
array[M_2] vector[N_2] z_2; // standardized group-level effects
vector<lower=0>[M_3] sd_3; // group-level standard deviations
array[M_3] vector[N_3] z_3; // standardized group-level effects
vector<lower=0>[M_4] sd_4; // group-level standard deviations
array[M_4] vector[N_4] z_4; // standardized group-level effects
vector<lower=0>[M_5] sd_5; // group-level standard deviations
array[M_5] vector[N_5] z_5; // standardized group-level effects
vector<lower=0>[M_6] sd_6; // group-level standard deviations
array[M_6] vector[N_6] z_6; // standardized group-level effects
///////////////////////////////////////////////////////////////////////////////////////
// latent imputed values for censored observations
vector<lower=Y[Jrcens[1:Nrcens]], upper=1>[Nrcens] Yright;
vector<lower=0, upper=Y[Jlcens[1:Nlcens]]>[Nlcens] Yleft;
vector<lower=Y[Jicens[1:Nicens]], upper=rcens[Jicens[1:Nicens]]>[Nicens] Yint;
///////////////////////////////////////////////////////////////////////////////////////
}
transformed parameters {
vector[N_1] r_1_1; // actual group-level effects
vector[N_2] r_2_1; // actual group-level effects
vector[N_3] r_3_1; // actual group-level effects
vector[N_4] r_4_zi_1; // actual group-level effects
vector[N_5] r_5_zi_1; // actual group-level effects
vector[N_6] r_6_zi_1; // actual group-level effects
real lprior = 0; // prior contributions to the log posterior
r_1_1 = (sd_1[1] * (z_1[1]));
r_2_1 = (sd_2[1] * (z_2[1]));
r_3_1 = (sd_3[1] * (z_3[1]));
r_4_zi_1 = (sd_4[1] * (z_4[1]));
r_5_zi_1 = (sd_5[1] * (z_5[1]));
r_6_zi_1 = (sd_6[1] * (z_6[1]));
lprior += student_t_lpdf(Intercept | 3, 0, 2.5);
lprior += gamma_lpdf(phi | 0.01, 0.01);
lprior += logistic_lpdf(Intercept_zi | 0, 1);
lprior += student_t_lpdf(sd_1 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
lprior += student_t_lpdf(sd_2 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
lprior += student_t_lpdf(sd_3 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
lprior += student_t_lpdf(sd_4 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
lprior += student_t_lpdf(sd_5 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
lprior += student_t_lpdf(sd_6 | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
}
model {
// likelihood including constants
if (!prior_only) {
// initialize linear predictor term
vector[N] mu = rep_vector(0.0, N);
// initialize linear predictor term
vector[N] zi = rep_vector(0.0, N);
mu += Intercept + Xc * b;
zi += Intercept_zi + Xc_zi * b_zi;
for (n in 1:N) {
// add more terms to the linear predictor
mu[n] += r_1_1[J_1[n]] * Z_1_1[n] + r_2_1[J_2[n]] * Z_2_1[n] + r_3_1[J_3[n]] * Z_3_1[n];
}
for (n in 1:N) {
// add more terms to the linear predictor
zi[n] += r_4_zi_1[J_4[n]] * Z_4_zi_1[n] + r_5_zi_1[J_5[n]] * Z_5_zi_1[n] + r_6_zi_1[J_6[n]] * Z_6_zi_1[n];
}
mu = inv_logit(mu);
zi = inv_logit(zi);
///////////////////////////////////////////////////////////////////////////////////////
// Uncensored data
for (i in 1:Nevent) {
int n = Jevent[i];
target += zero_inflated_beta_lpdf(Y[n] | mu[n], phi, zi[n]);
}
// Right-censored
for (i in 1:Nrcens) {
int n = Jrcens[i];
target += zero_inflated_beta_lpdf(Yright[i] | mu[n], phi, zi[n]);
}
// Left-censored
for (i in 1:Nlcens) {
int n = Jlcens[i];
target += zero_inflated_beta_lpdf(Yleft[i] | mu[n], phi, zi[n]);
}
// Interval-censored
for (i in 1: Nicens) {
int n = Jicens[i];
target += zero_inflated_beta_lpdf(Yint[i] | mu[n], phi, zi[n]);
}
}
///////////////////////////////////////////////////////////////////////////////////////
// priors including constants
target += lprior;
target += std_normal_lpdf(z_1[1]);
target += std_normal_lpdf(z_2[1]);
target += std_normal_lpdf(z_3[1]);
target += std_normal_lpdf(z_4[1]);
target += std_normal_lpdf(z_5[1]);
target += std_normal_lpdf(z_6[1]);
}
generated quantities {
// actual population-level intercept
real b_Intercept = Intercept - dot_product(means_X, b);
// actual population-level intercept
real b_zi_Intercept = Intercept_zi - dot_product(means_X_zi, b_zi);
}
The reason for the modification was that the brms model was really struggling to sample. The modified model finished sampling fast (considering the amount of data and model complexity), without issues and had good Rhats and Bulk_ESS values. Some more details here.
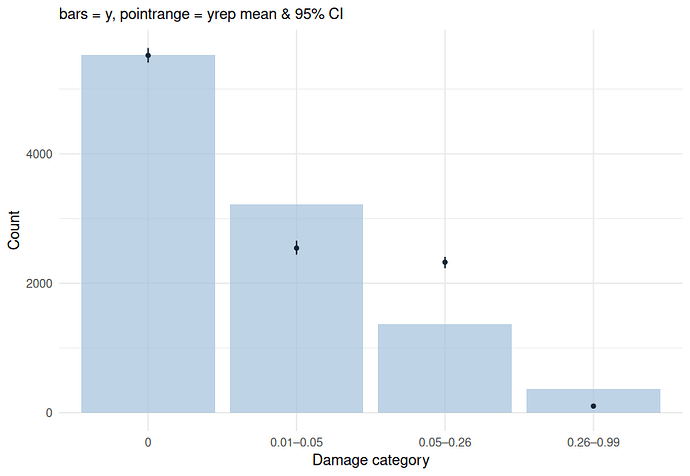
I am not sure what would be a good way to do a posterior predictive check for such a model. What I have tried is to generate predictions, impose on them the same interval censoring scheme and compare.
ppc = function(fit, data, ndraws = 10) {
observed = case_when(data$invert_damage.perc == 0 ~ "0",
data$invert_damage.perc < 6 ~ "0.01–0.05",
data$invert_damage.perc < 26 ~ "0.05–0.26",
data$invert_damage.perc >= 26 ~ "0.26–0.99")
ypred = posterior_predict(fit, ndraws = ndraws)
bins = function(x) {
case_when(x == 0 ~ "0",
x < 0.06 ~ "0.01–0.05",
x < 0.26 ~ "0.05–0.26",
x >= 0.26 ~ "0.26–0.99")
}
sim_bins = apply(ypred, 1, function(x) table(factor(bins(x),
levels = c("0",
"0.01–0.05",
"0.05–0.26",
"0.26–0.99"))))
sim_df = as.data.frame(t(sim_bins))
sim_df$draw = 1:nrow(sim_df)
obs_counts = table(factor(observed,
levels = c("0",
"0.01–0.05",
"0.05–0.26",
"0.26–0.99")))
obs_df = data.frame(Category = names(obs_counts),
Observed = as.numeric(obs_counts))
sim_summary = sim_df %>%
pivot_longer(cols = -draw,
names_to = "Category",
values_to = "Simulated") %>%
group_by(Category) %>%
summarise(mean = mean(Simulated),
lower = quantile(Simulated, 0.025),
upper = quantile(Simulated, 0.975))
plot_df = left_join(obs_df, sim_summary, by = "Category")
ggplot(plot_df, aes(x = Category)) +
geom_col(aes(y = Observed), fill = "#a2c0d9", alpha = 0.7) +
geom_pointrange(aes(y = mean, ymin = lower, ymax = upper),
color = "#152736", size = .25, fatten = 2) +
labs(y = "Count", x = "Damage category",
subtitle = "bars = y, pointrange = yrep mean & 95% CI") +
theme_minimal()
}
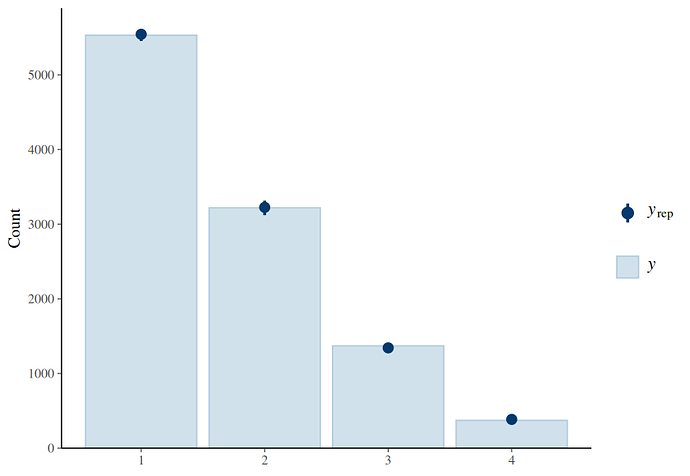
Do you think this is a valid approach to evaluate the model? The result is not particularly encouraging. I have also used a cumulative probit model (four levels, same predictors), which seemed to do a much better job: