Parallel autodiff v3

Developers
1

Hi!

The discussions on parallel autodiff v2 lead to a few considerations

  1. we really would like to run the parallel phase to also run during the reverse sweep
  2. we concentrate on the reduce sum only => so only a single output
  3. we want to keep track of all var’s which are part of anything running parallel => this means we cannot use closures which have any var in them (@Bob_Carpenter I hope we can have a flag for the closures indicating if these capture data only)

With all these points we can actually code a map_rect style thing which only relies on our current nested AD. At least this is what I think can be done. However, the down-side is that quite a few vari’s need to be copied around and moreover to make this thing convenient to use we need to use C++ tuples to make use of the ... magic thing… and here I would very much appreciate help. More details below.

The best news is: This can be implemented on the back of our current AD system. No need to refactor the thing!

The only bad news is that this technique can likely not be used for higher-order autodiff, but oh well… if you need parallelism then you probably anyway cannot afford higher-order derivatives (which would anyway be better off being parallelized differently, I think).

What I have done is to code up a basic prototype with a restricted interface geared toward the example I use, a hierarchical poisson log-lik. For this case I did

  • test that we get correct derivatives with/without threading…looks good
  • test that nested parallelism works… it does
  • write a benchmark to test if the extra copying work is harming us or not…its not so much harming (and can even be improved with more clever coding)

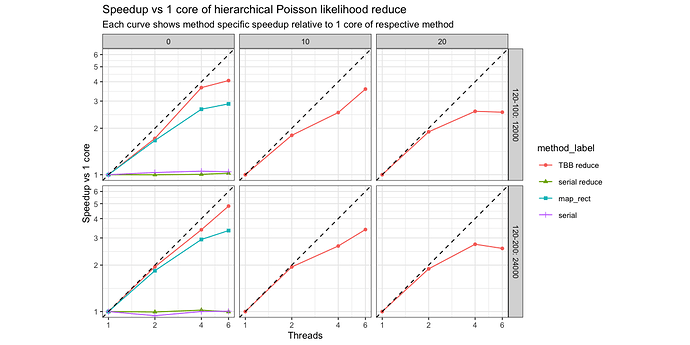
The benchmark results are for 12 \cdot 10^3 terms of a normalized log-likelihood which is grouped in 10 (dense) or 100 (sparse) groups. The dense case represents lots of data per group and this implies less copying overhead than the sparse case. I wanted to see how bad the copying overhead is hurting us… as there is not much of a difference we are fine from my perspective here.

The benchmarks are run with the perf-math repository on my 6-core MacBook Pro. So this is the profiled call to the grad call which should reflect the net speedup in an actual Stan model.

execution_time
execution_time1944×1200 173 KB

execution_speedup_serial
execution_speedup_serial1944×1200 170 KB

So we get quite decent speedups here which are totally usable. I should have the time next year to run the respective Stan model with this.

What is left?

I would really need a few hands here to help me out with the C++ magic which needs to happen to make this function a convenient function to use… and folks from the stanc3 compiler hopefully can also join to bind this to the Stan language.

The files are on the stan-math repo in the proto-parallel-v3 branch:

The benchmarks are from here. The repo contains, I think, all what is needed to get the above plots.

I am tagging a few people who I know are good with C++ magic for these tuples + type wrangling… @andrjohns @bbbales2 @tadej @stevebronder … sorry if I forgot you.

Should we drop the v2 parallel autodiff refactor thing? If all of what I did is correct… then probably the answer is yes for the moment being. Refactoring the AD sub system turns out to be a minefield. It takes a lot of energy from quite a few people to get this over, so it’s good if we can stay with what we have.

Happy new year!

Best,
Sebastian

5 Likes
2

This is talking about the need for placeholder vars so that when we have multiple grads() running we don’t have any race conditions?

When different threads start nested stacks, are those separate from the main stack? Is this what makes this work?

That’s fine with me.

+1 Excellent New Year reference

I looked at the current C++. Without actually understanding what the TBB stuff is, I like it. I am curious what’s possible at the interface level. I guess that’ll determine what C++ we need to write. I’m happy to help with the coding here.

Yeah, I am curious here what options we have.

Just to refresh, the inputs would be similar to map rect? Except now the inside function should return a scalar and we’re going to accumulate it?

I vaguely remember from a long time ago (I think this: Parallel reduce in the Stan language) that there may have been some different goals at the interface as a result of TBB doing the scheduling for us (but I forget what these were).

So roughly we were replacing something like:

for(n in 1:N) {
  target += some_lpdf(as[n], ...)
}

with:

target += parallel_map_reduce(some_lpdf, as, ...)

and there are shared params and whatnot in the (…).

@seantalts and @Bob_Carpenter, the goal here is to provide automatic parallelism for functions that act like lpdfs (all functions return a scalar and they all get added up). I assume what is possible right now looks a lot like map_rect, and eventually we want to take advantage of closures to make the interface clean.

So there’s reasons those functions would take all sorts of different things. And we get the packing/unpacking problem.

In the interim, is there anything fancier we can do with an interface like this with the new compiler?

3

Also thanks for putting this together with benchmarks and stuff so quickly!

4

Does automatic mean the user still controls it by calling a function, e.g. your parallel_map_reduce(some_lpdf example? What would your dream interface to it look like? That one seems reasonable to me because it lets a user manually mark where they’d like to use parallelism (which I think is a required escape hatch for any parallelism system), and will take some serious compiler work to get closures to pack/unpack correctly (needs to be done anyway). We could aim for using @rybern’s factor graphs to automatically parallelize stuff with some compiler flag as well, but I’m not sure that would completely replace manual controls.

5

The parallelization would be controlled by a function call, yeah.

So like if this were R, something like:

sum(sapply(my_list, my_function))

parallel_map_reduce would handle the parallelism internally. It’d be a blocking call, so it doesn’t return until it’s done.

Yeah, I think this is more the direction I was going. Do you see any opportunities to getting stuff into these functions easier than map_rect? Closures eventually, but were tuples gonna be in the new compiler or anything like that?

6

Maybe. If you look at the C++ code you see that the user functor is passed in as type only. This guarantees that there is no internal state (any var) in the functor over which we do not have any control. This is the same logic as used for map_rect. This way it is guranteed that every variable needed to call the functor is passed in as argument such that we know about it (and things do not hide in a closure).

It works exactly like map_rect. So the work chunks are executed on one of the threads available to the TBB (this can include the “main” thread). Each of these work chunks will start_nested and then stop the nesting after its done. The results are stored as doubles (the value of the aggregated sum and the partials of the arguments). On the main thread we then call the “build” method of the operands_and_partials such that only there the result gets added to the AD tape.

No. I really want to free the users from packing / unpacking. So I definitely want to use so-called C++ parameter packs. I added a lengthy comment in the C++ which describes what I have hard-coded now and what we need to engineer.

Correct. The ... is super important so that users can pass in their data structures in their shapes and forms as they wish to use to code up their model. No more packing is a hard design goal for me. Only then users will start using this a lot more.

I am not sure why we get packing/unpacking problems. If we manage to wrangle the parameter packs, see here, which is a C++11 feature, then we can free the users (and the compiler as well) from packing / unpacking. It will require some nasty C++ plumbing though (probably similar to what you have done for adj_jac_apply?).

The stanc3 compiler should allow for variable length functions (so the number of arguments is flexible). See my comment in C++

/*
 * The ReduceFunction is expected to have an operator with the
 * signature
 *
 * inline T operator()(std::size_t start, std::size_t end,
 *                     std::vector<int>& sub_slice, std::vector<T>& lambda,
 *                     const std::vector<int>& gidx) const
 *
 * So the input data is sliced into smaller pieces and given into the
 * reducer. Which exact sub-slice is given to the function is defined
 * by start and end index. These can be used to map data to groups,
 * for example. It would be good to extend this signature in two ways:
 *
 * 1. The large std::vector which is sliced into smaller pieces should
 *    be allowed to be any data (so int, double, vectors, matrices,
 *    ...). In a second step this should also be extended to vars
 *    which will require more considerations, but is beneficial. One
 *    could leave this generalization to a future version.
 *
 * 2. The arguments past sub_slice should be variable. So the
 *    arguments past sub_slice would need to be represented by the
 *    "..." thing in C++. The complication for this is managing all
 *    the calls.
 *
 * So the parallel_reduce_sum signature should look like
 *
 * template <class ReduceFunction, class InputIt, class T, ...>
 * constexpr T parallel_reduce_sum(InputIt first, InputIt last, T init,
 *                                std::size_t grainsize, ...)
 *
 * which corresponds to a ReduceFunction which looks like
 *
 * inline T operator()(std::size_t start, std::size_t end,
 *                     std::vector<InputIt*>& sub_slice, ...)
 *
 * Note that the ReduceFunction is only passed in as type to prohibit
 * that any internal state of the functor is causing trouble. Thus,
 * the functor must be default constructible without any arguments.
 *
 */
template <class ReduceFunction, class InputIt, class T, class Arg1>
constexpr T parallel_reduce_sum(InputIt first, InputIt last, T init,
                                std::size_t grainsize, std::vector<Arg1>& varg1,
                                const std::vector<int>& idata1) {

Actually, I thought about making entire Stan models use this. So if we could ask users to write their model block such that the model block does not always accumulate log-prob over all summands, but over a sub-set which we can control from the outside, then that would be great… but it’s probably easier to let users write a model block which just calls parallel_reduce_sum.

I hope the above C++ comment is sufficient to understand how this is supposed to work. I am currently putting together a real Stan model. I am happy to add these files to some branch on github so that you can see how one would put it together when using a bit of C++ user functions.

7

Oh I’m happy to go with this. Definitely something I’d prefer too.

So in map rect we passed in arrays of things. Is the situation now that every mapped function gets the exact same arguments and then figures out on its own which data it needs to access with the first/last iterators?

So:

target += parallel_map_reduce(my_lpdf, a1, a2, a3, ...)

Would be equivalent to the original:

for(n in 1:N) {
  target += my_lpdf(a1, a2, a3, ...)
}

Ideally I’d be able to parallelize things like (this is code generated by brms – so really I’d like brms to parallelize things like):

vector[N] mu = temp_Intercept + Xc * b;
for (n in 1:N) {
  mu[n] += r_1_1[J_1[n]] * Z_1_1[n] + r_1_2[J_1[n]] * Z_1_2[n] +
    r_2_1[J_2[n]] * Z_2_1[n] +
    r_3_1[J_3[n]] * Z_3_1[n] + r_3_2[J_3[n]] * Z_3_2[n] +
    r_4_1[J_4[n]] * Z_4_1[n] +
    r_5_1[J_5[n]] * Z_5_1[n] +
    r_6_1[J_6[n]] * Z_6_1[n] + r_6_2[J_6[n]] * Z_6_2[n] +
    r_7_1[J_7[n]] * Z_7_1[n] + r_7_2[J_7[n]] * Z_7_2[n] +
    r_8_1[J_8[n]] * Z_8_1[n] +
    r_9_1[J_9[n]] * Z_9_1[n] +
    r_10_1[J_10[n]] * Z_10_1[n] +
    r_11_1[J_11[n]] * Z_11_1[n] + r_11_2[J_11[n]] * Z_11_2[n];
}

target += binomial_logit_lpmf(Y | trials, mu);

So that breaks down to:

  1. Compute N mus (can all be done independently)
  2. Evaluate binomial_logit_lpmf on each
  3. Accumulate them in target

And there are a toooooon of arguments. Xc is a matrix, all the r__ things are vectors and the Z__ things are vectors too.

8

Oh yeah maybe I messed that up. In your designs, the first two arguments are ranges, right?

So it’s we’re going for:

target += parallel_map_reduce(my_lpdf, a1, a2, a3, ...)

Which would replace:

target += my_lpdf(1, N, a1, a2, a3, ...)

Where the meaning of the first to arguments of my_lpdf are saying “compute and accumulate terms of this lpdf from 1 to N”

This is cause TBB will pass in start/stop indices to each of the lpdf calls?

9

Yes, with map rect people had to pack and unpack. In the new design people can use the start and end index to grab what they want from the shared parameters which we allow to be of any shape users wish them to be … then it will be easy for users to structure things according to their needs. However, there is one special argument, which is the first one. In my mind this is an array over whatever you want to iterate over. So in Stan we have

Custom_lpdf(1, N, big_array, a1, a2, …)

And our parallel reduce sum will make calls which look Like

Custom_lpdf(start, end, Slice_of_big_array, a1, a2, …)

We need this for efficiency. The thing with the shared parameters is that these get copied a lot, but the sliced big array will only be doubled in memory.

I can post tomorrow a working Stan model.

…and, yes, we should aim for @paul.buerkner and @bgoodri being happy with this so that it lands in the main r packages. This will scale the user base of this instantly to big N.

10

I need to see some examples to better understand how this would interact with what I am trying to do in brms. And, as @bbales pointed out, there may be a lot of arguments passed to custom_lpdf and I am not sure what parts of the brms Stan code I can re-write to evaluate in parallel and which parts we have to run serially in the end simply because writing the custom_lpdf would be too complex in a lot of cases.

11

Many programs have this structure, indeed. While it would be desirable to build up the “mu” vector with parallelism as well, this bit is not so performance critical in most cases, I think. The big chunk of work is happening in the lpmf call.

Here is a fully worked out Stan model example. It simulates fake data for a hierarchical poisson model and evaluates it in three flavors: new approach, map_rect, vanilla serial code. There is just one tuning parameter right now needed, which is the so-called “grainsize”. This tells the TBB how large the chunks should be. The value of “0” for grainsize let’s the TBB choose it automatically, which you can see from the benchmarks does not work really well. There is some guidance in the TBB doc on how to choose it.

The different columns in the plot are for different grainsize, the rows are for two problem sizes of 12 \cdot 10^3 and 24 \cdot 10^3 number of terms which are grouped into 100 groups.

method-relative-scale-poisson
method-relative-scale-poisson1200×600 97.1 KB

Files needed to run this:

If others want to play with it, I can probably make the script which generates these plots available in a way which makes it straightforward to run it.

In the meantime I have also refactored the C++ code a bit so that it is now a lot easier to work with.

Since this pattern is very useful, I think, we could actually consider realizing a simplified version now and build this out later. That would mean to fix the number of arguments now and to restrict the types somewhat which can be used in order to make coding this up simpler. In a later version we then make the types more flexible and allow for parameter packs. This could be realized quickly… unless more workforce with extensive knowledge on C++ parameter pack/meta programming/whatever else magic join this effort (though, I will at least give it a try to do the parameter packs).

2 Likes
12

This look great, definitely harvests a lot of the low hanging fruits. Let me know if I can help in any way. Once the kernel generator is finished we could extend this exact same for GPUs which would make GPUs usable outside the “big nodes” concept.

13

The looks great! I have a couple of questions to clarify the new design.

  1. Do I understand it correctly that hierarchical_reduce is the only function to be defined by the user in the end or does the user also have to define parallel_hierarchical_reduce themselves in the end?
  2. I don’t see y being sliced explictely but only log_lambda_group. Is it because the first argument will be automatically sliced according to start:end?
  3. Do I understand correctly that gidx is not necessary in general but just something you used to demonstrate the flexibility of your design?
  4. Would it be possible to define hierarchical_reduce also as an lpmf function directly that is with y (or y_slice) as first argument rather than start and end as first arguments?
14
  1. Yes, the user would only define hierarchical reduce. The parallel function would be a Stan provided function which you pass in the reduce function.
  2. The slicing is done automatically for the first argument. So the first argument is only passed in according to the sub range start to end. These are automatically determined by the tbb library.
  3. Gidx is only required for this problem to code this specific model. If I manage the c++ parameter packs then we can have an arbitrary number of arguments. … as many as you need for your problem.
  4. We can certainly discuss the order of the arguments. You are probably right in that start and end should not be first (then maybe last?)

I am glad you like it…let’s see how general we can get this to work.

15

Great, that sounds good to me.

  1. I think this is ok, but just for my benefit: Is there a way to do manual slicing for the first argument as well?
  2. I would be in favor of having start and end last.
16

No, you cannot control the slicing directly…but you can control what is being sliced over which is basically the control you are looking for.

We can discuss the arguments.

17

Hi!

@paul.buerkner Why would you want to control slicing? Can you give an example? I think you can always reorder/restructure things and choose your set of elements which are being sliced according to your needs (I hope).

The thing about what is being sliced is that only this argument gets copied in the small and sliced chunks into the functor. The shared arguments always get copied as a whole for every evaluation of the reduce function. So if the TBB decides for your problem to make C chunks. Then we will endup with a doubling of the input which is being sliced in memory, while the shared arguments get copied C times. That’s the crux.

With the benchmarks I posted I noticed that the TBB reduce overall walltime was not really good when compared to its competitors. So we should not only look at scaling, but also at the total wall time.

Below are bechmarks where I restructure the program such that the slicing is done over the groups. Since we have per group many observations, this is more efficient. I also added another method which is “serial reduce”. This is calling the reduce function which I pass to the TBB - it’s just doing the reduce in a single go, i.e. as if the TBB would be calling just one chunk.

method-relative-scale-poisson
method-relative-scale-poisson1200×600 70.2 KB

And here the total walltime per case:

reduce-sum-runtime-poisson-static
reduce-sum-runtime-poisson-static800×480 46.4 KB

So we see that the grainsize=0 is ok for this problem which makes sense as the slicing is over the groups which themselves generate a lot more work. I am quite happy with the results. We go from 22s down to less than 5s here with an approach which is manageable by users to write (I hope).

Wrt. to placing the start/end indices, I am still in favor of putting them upfront, because I see these additional indices as going with the thing which we sliced - so it should show up there, I think. Moreover, to use this facility efficiently we are probably anyway have to deviate a bit from our standards. If you used to write this

target += binomial_logit_lpmf(big_y| big_mu, n);

where we assume this is a random effects model so that big_mu is of the same length as big_y which often is the case in this setting. Then we really should write this:

## in-efficient, because big_mu (a costly var) gets copied for every evaluation
target += parallel_reduce_sum(binomial_reducer, big_y, big_mu, n);
## a lot more efficient as the big_mu is only doubled in memory, while the data big_y is cheap to copy many times
target += parallel_reduce_sum(binomial_reducer, big_mu, big_y, n);

I am almost leaning toward coding up a version where you can use 5 vectors or so (real arrrays) which would be hard-coded for the moment. In an updated version we can make the arguments flexible.

Sebastian

(side-note: the shared data arguments are not needed to be copied, but it’s a lot easier for me to code it up like this for now…others are welcome to improve the code, of course…but I doubt that avoiding copies of the data is a big performance drag at least in most Stan typical problems)

EDIT: I forgot to add the model generating the above benchmark:

18

Not sure if there are many use cases for controlling the slicing also of the first argument but one would be autoregressive models, in which we have to use former response values in the predictor term. Not sure if this would be any good use case for reduce at all, I just wanted to better understand the natural limitations of the proposal.

I understand your logic for putting start and end upfront and I am fine with that as well.

19

If you mean a model like this:

model {
  y[2:N] ~ normal(alpha + beta * y[1:(N - 1)], sigma);
}

then you can give as first argument to the reducer y[2:N] and as second argument y. This would slice up y[2:N] and you can pick what you need from the y argument. The y would be given as a full vector and you would pick y[start:end] out of it (due to the offset of 1 between those two arrays).

Copying y for each evaluation isn’t nice, but then this is only data for one; and in a later version we will almost for sure be able to avoid the copying of the data arguments.

Would that work?

20

Yes, indeed that would work by using y in two arguments. Thanks!