Ordinary least squares vs Stan: different results?

Modeling
1

I have a least squares inference problem, and wanted to replace my Stan program with WLS. However, for some data, I get very different results, which I find very puzzling (see also here or here).

I am providing a specific example, with 29 data points, and the results of least squares and Stan. I simplified the problem to homoscadastic errors (yerr=1, i.e., OLS). In blue is a plot of the data:
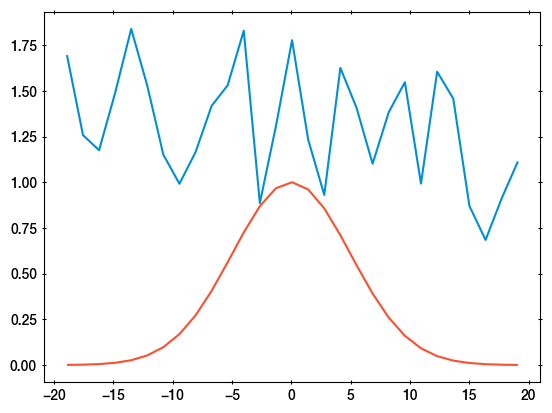
wls-data

I fit with three components: 1) a constant, 2) a linear component, 3) a fixed shape (red curve). The normalisations are free parameters called y0, k, norm. They receive flat, unconstrained priors.

Below is my code, data and analysis:

import numpy as np
import cmdstanpy
import matplotlib.pyplot as plt
import corner
from statsmodels.regression.linear_model import WLS

# data:

data = {'N': 29, 'x0': 5895.6,
	'weight': np.array([7.8281132e-04, 2.0987201e-03, 5.2415314e-03, 1.2138436e-02,
       2.6183469e-02, 5.2412681e-02, 9.7503543e-02, 1.6878714e-01,
       2.7118218e-01, 4.0531352e-01, 5.6230277e-01, 7.2535461e-01,
       8.6879617e-01, 9.6697074e-01, 9.9991941e-01, 9.6047860e-01,
       8.5685223e-01, 7.1017146e-01, 5.4648513e-01, 3.9075232e-01,
       2.5953308e-01, 1.5991287e-01, 9.1608725e-02, 4.8663702e-02,
       2.4034550e-02, 1.1002056e-02, 4.6862061e-03, 1.8525344e-03,
       6.7856628e-04]),
       'x': np.array([5876.689 , 5878.041 , 5879.3965, 5880.7485, 5882.1045, 5883.458 ,
       5884.8115, 5886.1685, 5887.5225, 5888.8804, 5890.235 , 5891.5933,
       5892.948 , 5894.304 , 5895.6636, 5897.02  , 5898.3794, 5899.737 ,
       5901.0967, 5902.4546, 5903.8125, 5905.174 , 5906.532 , 5907.894 ,
       5909.2534, 5910.616 , 5911.9756, 5913.336 , 5914.699 ]), 
      'y': np.array([1.6952891 , 1.2575909 , 1.1748848 , 1.488376  , 1.8385803 ,
       1.528486  , 1.1511977 , 0.9915795 , 1.1635164 , 1.4170816 ,
       1.5301417 , 1.8289143 , 0.8856548 , 1.3066483 , 1.7767009 ,
       1.2338594 , 0.93022835, 1.625354  , 1.4074879 , 1.1009187 ,
       1.3825897 , 1.546863  , 0.99267375, 1.6045758 , 1.4572536 ,
       0.8702313 , 0.68421644, 0.911552  , 1.1132364 ]), 
       'yerr': np.array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])}
data['dx'] = data['x'] - data['x0']

# plot the data
plt.plot(data['dx'], data['y'])
plt.plot(data['dx'], data['weight'])
plt.savefig('wls-data.pdf')
plt.close()


# run WLS
# prepare WLS matrix
A = np.column_stack((np.ones(data['N']), data['dx'], data['weight']))
wls_results = WLS(data['y'], A, data['yerr']**-2).fit()
# wls_results = OLS(data['y'], A).fit()   # this gives the same results
params = wls_results.params
cov_matrix = wls_results.cov_params()
y0_fit, k_fit, norm_fit = params
y0_err, k_err, norm_err = np.sqrt(np.diag(cov_matrix))

# run Stan
# write the Stan code to a file
stan_code = """
data {
  int N;            // number of data points
  vector[N] dx;     // x data points
  vector[N] y;      // y data points
  vector[N] yerr;   // y uncertainty
  vector[N] weight; // weight describing feature shape
}
parameters {
  real y0;     // continuum normalisation
  real k;      // continuum slope
  real norm;   // feature strength
}
model {
  // assume Gaussian measurement errors
  y ~ normal(y0 + k * dx + norm * weight, yerr);
}
"""
model_name = 'wls'
filename = 'wls.stan'
with open(filename, 'w') as fout:
	fout.write(stan_code)

sm = cmdstanpy.CmdStanModel(stan_file=filename, model_name=model_name)
fit = sm.sample(data=data, iter_sampling=100000, iter_warmup=4000, chains=4, show_console=False, show_progress=True)
print(fit.summary())
print(fit.diagnose())
norm = fit.stan_variable('norm')
y0 = fit.stan_variable('y0')


# plot results:
corner.corner(
	np.transpose([y0, fit.stan_variable('k'), norm]), labels=['y0', 'k', 'norm'],
	plot_datapoints=False, plot_density=False, levels=np.exp(-np.arange(5)))
corner.corner(
	np.random.multivariate_normal(params, cov_matrix, size=len(norm)), labels=['y0', 'k', 'norm'],
	fig=plt.gcf(), color='b', plot_datapoints=False, plot_density=False, levels=np.exp(-np.arange(5)))
plt.savefig('wls_corner.pdf')

# compare means and errors of the two techniques:
print(' same norm?', norm_fit, norm.mean(), 'err:', norm_err, norm.std())
print(' same y0?', y0_fit, y0.mean(), 'err:', y0_err, y0.std())

The Stan diagnostics are all ok, and Rhat is 1.

I get the same means (first two numbers), but much larger uncertainties with Stan:

 same norm? 0.11509463050765173 0.11374671140722921 err: 0.15857910773382997 0.5286261376859842
 same y0? 1.2708374766432424 1.2714545692049999 err: 0.07524091396160146 0.25075389547048704

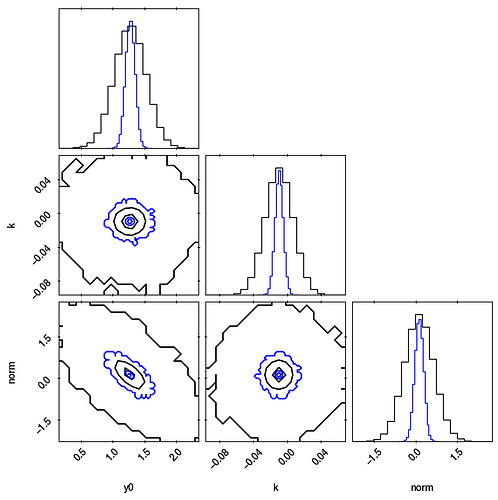
Here is a pairs/corner plot comparing the results from Stan (black) to the least squares covariance (blue):

wls_corner
wls_corner714×716 33.7 KB

Why do the results not coincide in this setting?

2

Nevermind, I found the bug. I was using statsmodels incorrectly.

The covariance needs to be scaled by wls_results.scale.

Changing the line
cov_matrix = wls_results.cov_params()
to
cov_matrix = wls_results.cov_params() / wls_results.scale
gives consistent results between the Stan code and least squares.

3

Why is the model given by

y ~ normal(y0 + k * dx + norm * weight, yerr);

In particular, why are you multiplying norm*weight in the stan version? Usually, weighted least squares is equivalent to dividing the errors by the weight (in the WLS docs, this is described in the inverse way, “If you supply 1/W then the variables are pre- multiplied by 1/sqrt(W).” (I’m also unclear on your weight vs sqrt(weight).)

4

Sorry, this is a poorly chosen variable name. I did not use weight in the Stan code for the errors. The errors are stored in yerr, which is 1 in this example. weight is the shape of one component (red curve in the first plot).