New to Stan - trying to estimate individual-level data using Bayesian inference

General
,
1

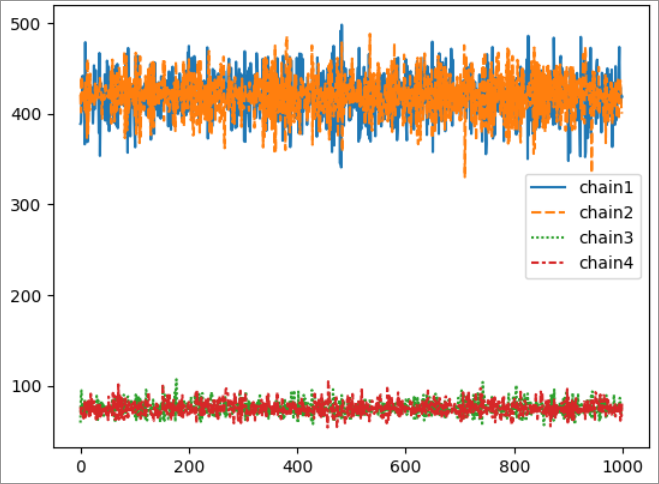
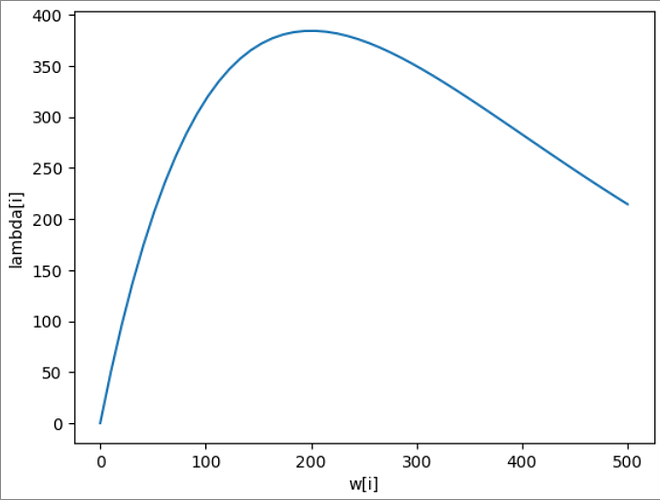
I am brand new to Bayesian inference, Stan and Rstan. I am attempting to infer individual-level worm burdens based on individual-level egg outputs, initially just with very simple dummy data. I have generated dummy data:

#generate dummy data for worm counts, based on a negative binomial distribution
worms <- rnbinom(1000, size = 0.5, mu = 20)

#density dependence of fecundity in worms
lambda <- ifelse(worms > 0, 5.2*worms*exp((worms - 1)*-0.005), 0)

#now use worm data to generate egg counts per individual
eggs <- rpois(length(worms), lambda)

I then set up a simple stan model:

// data block
data {
  int<lower = 0> N;
  array[N] int<lower = 0> egg_count; // egg count data
  real<lower = 0> fec; // worm fecundity
  real dd; // density dependence term
}

// parameter block
parameters {
  array[N] real<lower = 0> worms; // estimate worm number
}

// model block
model {
  // no priors
  // likelihood function
  for (i in 1:N) {
    egg_count[i] ~ poisson(fec*worms[i]*exp((worms[i] - 1)*dd)); // egg count is poisson distributed based on worms * fecundity * density dependence
  }
}

I then run the model using RStan:

#prepare dataset to pass to stan
worm_data <- list(N = length(eggs),
                  egg_count = eggs,
                  fec = 5.2,
                  dd = -0.005)

#run model
wb.model <- stan(
  file = "X.stan",
  data = worm_data,
  iter = 30000,
  chains = 3,
  verbose = FALSE
)

Weirdly, the model is able to infer worm burdens well at low egg count values, but does not converge at higher egg count values. I have tried increasing the iterations on the model, but it still does not converge.

What am I doing wrong?

Thanks in advance for the help.