Hi,
I am using the brms package in R (version 4.3.0) to fit a two-level cross-classified random intercepts only mixed effects location-scale model to ratings data. My MELS model is
mod0 <- brm(bf(dbr ~ 1 + T2 + T3 + (1 | tch) + (1 | stu),
sigma ~ 1 + T2 + T3 + (1 | tch) + (1 | stu)),
iter = 10000,
chains = 4,
cores = 4,
control = list(adapt_delta=0.90),
data = df)
The issue is when looking a posterior distributions for certain parameters, the chains show no variation from the starting value. Here’s an example of what I’m seeing:
The location covariates T2 and T3 appear acceptable but posteriors for all other parameters look similar to the location and scale intercepts seen in the image above. I tried troubleshooting: increased number of iterations from default to 10,000, increased adapt_delta from default to .90, simplified the model by dropping correlations between location/scale random effects. None of these fixed the issue. I am currently running a model with stronger priors to determine if this is an identification issue. If that doesn’t work… Any ideas what may be causing this?
Thanks in advance,
-Jennifer
2 Likes
Can you say more about the data? For example: What are T2, T2, tch (teacher?) & stu (student?); how many unique values of tch and stu are there; and how many observations per tch / stu? It will also help to show plots of the variation you are modeling. For example, the posterior estimate for the b_T2 and b_T3 location params is effectively zero but it’s not clear whether that’s due to the convergence issues or it’s what the data indicates.
1 Like
Of course. These are teacher ratings of student behavior using the Direct Behavior Ratings (DBR) scale. Students were rated twice per day (morning and afternoon) for five days in the fall, winter, and spring of a single academic year. The composite rating score ranged from 0-30. Total numer of observations is 7113, number of teachers = 61 and number of students = 583 after removing missing responses. Since students generally received the same rating in the morning and afternoon, I took the average of the two ratings for each day. Teachers (tch) should have rated the same 10 students (stu) each time period. Each teacher should have assigned 150 daily average ratings for the academic year and each student should have 15 daily average ratings for the year. But there were missing responses. The table below gives the mean, min, and max number of observations for teacher and student.
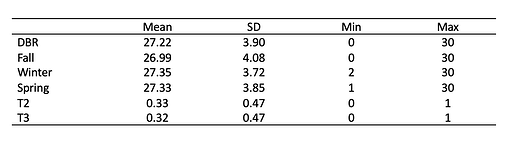
There was little change in slope across all 15 time points (five avg daily ratings per data collection period). So I looked at change in intercept between daily collection periods. T2 and T3 are the difference in ratings from Fall to Winter (T2) and Fall to Spring (T3), respectively. Below is a table of descriptive statistics for the variables in the data set.
Below are plots of residual variance distribution for 20 teachers (first plot) and distribution plots for 30 students (second plot)
1 Like
Thank you for the detailed description; this is an interesting study. Although your ultimate goal is to fit the MELS model, it might be helpful – though also more work – to start with a simpler model on an aggregate version of your dataset, get that model to converge and fit well, and then expand the model / data in consecutive steps. For example, perhaps you can start by averaging the 5 ratings per quarter into a single rating & dropping the winter and spring indicators T2 and T3. I would also consider simplifying the variance formula until I get the model to converge. This process may make it a bit easier to figure out what kind of priors to choose as well.
Also it seems that the structure might be nested (students within teachers); that’s how I understand the statement “teachers rated the same 10 students”. If these effects are indeed nested, then this can be specified with (1 | tch / stu).