Jacobian of softmax tansformation of a (n-1 degrees of freedom) unbounded parameter

[stemangiola]

Hello Community,

I have a dirichlet regression

simplex_parameter ~ dirichlet(softmax(X * alpha_parameter) * phi_parameter)

I would like to compare MC with variational bayes, however Isuppose this does not play well with a posterior that is beta shaped (bounded at 0,1). Using unbouded parameter (with the right n-1 degrees of freedom) might make it more compativle with variational (?).

softmax(n_minus_1_df_parameter) ~ dirichlet(softmax(X * alpha_parameter) * phi_parameter);

// jacobian ...

Hence, my question about variable transformation.

[stemangiola]

Sorry for tagging you directly, but I was wondering if @Bob_Carpenter or @avehtari had some advise on this.

(@martinmodrak)

[martinmodrak]

I am not sure I understand exactly what you are after but (Jacobian of) transformations between spaces with different dimensions were discussed at: Non-invertible change of variables?

Is this what you are after?

Best of luck!

[stemangiola]

As far as I can understand (please @betanalpha correct if wrong )

there is one-to-one correspondence between

an unbounded (-Inf, Inf) vector with n-1 degrees of freedom, and a simplex.

I was imagining that softmax transformation would require some Jacobian correction similar to the log transformation.

[betanalpha]

See https://arxiv.org/abs/1010.3436. The Stan manual also has a derivation based on the stick breaking process, or at least it used to.

[stemangiola]

@andrjohns I tried to implement your jacobian correction in a dummy model. Considered my still very poor knowledge on the matter, I was wondering if you could guess why it is not converging.

Model using simplex

transformed data{    vector[4] alpha = [1,2,3,4]';     }
parameters{	         simplex[4] prop;                  }
model{               prop ~ dirichlet(alpha);          }

Model using softmax

functions{
    vector sum_to_zero(vector v){
    	int K = rows(v)+1;
    	vector[K] v_0;
	
    	v_0[1:(K-1)] = v;
    	v_0[K] = -sum(v_0[1:(K-1)]);
	
	    return(v_0);
    }
}
transformed data{
	int K = 4;
	int N = 1;

	vector[K] alpha = [1,2,3,4]';
	matrix[K,K] ident = diag_matrix(rep_vector(1,K));
}
parameters{     vector[K-1] rate_raw;    }
transformed parameters{
	simplex[K] prop[N];
	prop[1] = softmax(sum_to_zero(rate_raw));
}
model{
    for(n in 1:N) {
    	matrix[K,K] jacobian;
    	prop[n] ~ dirichlet(alpha);
	
    	for(i in 1:K) {  for(j in 1:K) {
    		jacobian[i,j] = prop[n,i] * (ident[i,j] - prop[n,j]);
        }}

    	target += log_determinant(jacobian);
    }
}

There were 2075 divergent transitions after warmup.

Thanks!

[andrjohns]

This will be something to call in someone with deeper knowledge for.

@betanalpha we’re trying to implement the jacobian correction for giving a prior to the softmax of a vector, but sampling is terrible.

Where the Jacobian of the softmax s(x) is given by:

J_x(s) = \text{diag}(s) - ss^T

A reproducible example is below:

stancode = "data {
  int K;
}

transformed data{
  vector[K] alpha = [1,2,3,4]';
  matrix[K,K] ident = diag_matrix(rep_vector(1,K));
}

parameters{
 vector[K] prop;
}

transformed parameters {
  simplex[K] prop_soft = softmax(prop);
}

model{
  prop_soft ~ dirichlet(alpha);

  target += log_determinant(diag_matrix(prop_soft) - prop_soft*prop_soft');
}"

mod = stan(model_code=stancode,data=list(K=4))

Is there a step we’ve missed here?

[betanalpha]

The sampling is terrible because that model is over-parameterized. Multiplying all elements of prop by a constant yields the same prop_soft, and because the target density depends only on prop_soft it will be invariant to such scalings. Consequently the target density will be non-identified and nearly impossible to completely sample.

Note that there is a more general, well-known result – if each exp(prop) follows a distribution specified by a gamma density function with shape parameter \alpha_{n} then the pushforward distribution of prop_soft will be given by a Dirichlet density with parameters \{\alpha_{1}, \ldots, \alpha_{N} \}. This can be useful for forward sampling but it’s not very useful for inference due to the inherent degeneracy.

[stemangiola]

@betanalpha

The sampling is terrible because that model is over-parameterized. Multiplying all elements of prop by a constant yields the same prop_soft , and because the target density depends only on prop_soft it will be invariant to such scalings. Consequently the target density will be non-identified and nearly impossible to completely sample.

If I’m not mistaking you are referring to that prop must have K-1 degrees of freedom. I have implemented the non-overparametrised model but we still get non-convergence.

Is it possible we are doing some trivial mistake in the implementation of the jacobian?

functions{
	vector sum_to_zero(vector v){
		int K = rows(v)+1;
		vector[K] v_0;
		
		v_0[1:(K-1)] = v;
		v_0[K] = -sum(v_0[1:(K-1)]);
		
		return(v_0);
	}
}
transformed data{
  int K = 4;
  vector[K] alpha = [1,2,3,4]';
  matrix[K,K] ident = diag_matrix(rep_vector(1,K));
}
parameters{  vector[K-1] prop; }
transformed parameters {
  simplex[K] prop_soft = softmax(sum_to_zero(prop));
}
model{
  prop_soft ~ dirichlet(alpha);
  target += log_determinant(diag_matrix(prop_soft) - prop_soft*prop_soft');
}

Afterall if I ignore the Jacobian the model “kind of” works (obviously with some divergencies)

functions{
	vector sum_to_zero(vector v){
		int K = rows(v)+1;
		vector[K] v_0;
		
		v_0[1:(K-1)] = v;
		v_0[K] = -sum(v_0[1:(K-1)]);
		
		return(v_0);
	}
}
transformed data{
  int K = 4;
  vector[K] alpha = [1,2,3,4]';
}
parameters{  vector[K-1] prop; }
transformed parameters {  simplex[K] prop_soft = softmax(sum_to_zero(prop));  }
model{    prop_soft ~ dirichlet(alpha);    }

---

P.S. One of the goals of using uncontrained + jacobian implementation is to allow this model

transformed data{    vector[4] alpha = [1,2,3,4]';     }
parameters{	         simplex[4] prop;                  }
model{               prop ~ dirichlet(alpha);          }

To be more amenable to variational bayes, with the prop parameter being more symetric/normal-like

[betanalpha]

Something is definitely wrong in the first implementation – it looks like the adaptation is failing. It could be numerical problems. You’ll have to follow up with careful investigation of the diagnostics and Hamiltonian Monte Carlo statistics.

[stemangiola]

@andrjohns actually it’s strange that

First implementation you proposed was looking like this

jacobian[i,j] = prop[n,i] * (ident[i,j] - prop[n,j]);

Second, the ident matrix disappeared

diag_matrix(prop_soft) - prop_soft*prop_soft'

is possible that a typo happened?

[andrjohns]

No, they’re mathematically identical. The second form is just a more concise expression.

Consider the 2-element case as an example:

diag(s) - ss^T

Expands to:

\begin{bmatrix}s_1 & 0 \\0 & s_2 \end{bmatrix} - \begin{bmatrix}s_1^2 & s_1s_2 \\s_2s_1 & s_2^2 \end{bmatrix}

\begin{bmatrix}s_1 -s_1^2 & -s_1s_2 \\-s_2s_1 & s_2 - s_2^2 \end{bmatrix}

Which is the same as:

\begin{bmatrix}s_1 (1-s_1) & s_1(0-s_2) \\s_2(0-s_1) & s_2(1 - s_2) \end{bmatrix}

Which is what the loop with an identity matrix was expressing

[stemangiola]

With limited knowledge in Jocabians it comes hard to even “poke” the statement to see what part can cause such abrupt failure.

afterall it’s just one line of code :)

[stemangiola]

@andrjohns

Where the Jacobian of the softmax s(x)s(x) is given by:

Jx(s)=diag(s)−ssT

Could you please point me to a reference where the above is described? I will try to investigate a bit better and maybe try stackexchange

[andrjohns]

Sure, there are two references I used for this:

Softmax with cross-entropy

The Softmax function and its derivative - Eli Bendersky's website

[stemangiola]

Thanks a lot,

this model “works” (with some divergencies caused by extreme correlation of parameters that I will try to solve with)

there was apossible mistake in this prop_soft*prop_soft' instead of prop_soft'*prop_soft

functions{
	vector sum_to_zero(vector v){
		int K = rows(v)+1;
		vector[K] v_0;
		
		v_0[1:(K-1)] = v;
		v_0[K] = -sum(v_0[1:(K-1)]);
		
		return(v_0);
	}
}
transformed data{
  int K = 4;
  vector[K] alpha = [1,2,3,4]';
  matrix[K,K] ident = diag_matrix(rep_vector(1,K));
}
parameters{  vector[K-1] prop; }
transformed parameters {
  simplex[K] prop_soft = softmax(sum_to_zero(prop));
}
model{
  prop_soft ~ dirichlet(alpha);
  //target += log_determinant(diag_matrix(prop_soft) - prop_soft'*prop_soft);
}

[andrjohns]

there was apossible mistake in this prop_soft*prop_soft' instead of prop_soft'*prop_soft

Unfortunately that’s not the case. prop_soft*prop_soft' gives a K x K matrix, whereas prop_soft'*prop_soft gives a 1 x 1 matrix:

The notation in the link above used s^Ts because they were treating the softmax as returning a row-vector

[stemangiola]

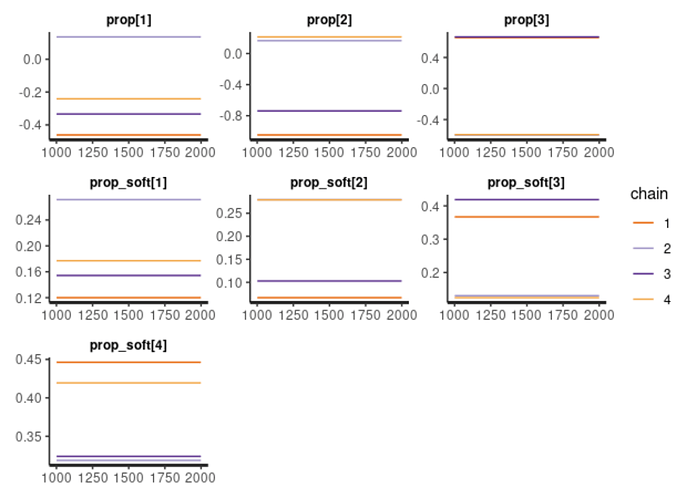
OK what is puzzling me that if I use this model with no jacobian, and with QR approach to N-1 degrees of freedom vector (Test: Soft vs Hard sum-to-zero constrain + choosing the right prior for soft constrain).

functions{
vector Q_sum_to_zero_QR(int N) {
    vector [2*N] Q_r;

    for(i in 1:N) {
      Q_r[i] = -sqrt((N-i)/(N-i+1.0));
      Q_r[i+N] = inv_sqrt((N-i) * (N-i+1));
    }
    return Q_r;
  }

  vector sum_to_zero_QR(vector x_raw, vector Q_r) {
    int N = num_elements(x_raw) + 1;
    vector [N] x;
    real x_aux = 0;

    for(i in 1:N-1){
      x[i] = x_aux + x_raw[i] * Q_r[i];
      x_aux = x_aux + x_raw[i] * Q_r[i+N];
    }
    x[N] = x_aux;
    return x;
  }
}
transformed data{
  int K = 4;
  vector[K] alpha = [1,2,3,4]';
  matrix[K,K] ident = diag_matrix(rep_vector(1,K));
  
  vector[2*K] Q_r = Q_sum_to_zero_QR(K);
  real x_raw_sigma = inv_sqrt(1 - inv(K));
}
parameters{  vector[K-1] prop; }
transformed parameters {
  simplex[K] prop_soft = softmax(sum_to_zero_QR(prop, Q_r));
}
model{
  prop_soft ~ dirichlet(alpha);
  prop ~ normal(0, x_raw_sigma);
}```

```r
fit2 = stan(model_code=stancode, cores=4, iter = 10000, warmup = 1000)

I get same marginal posterior of the simplex compared to the the source model

transformed data{    vector[4] alpha = [1,2,3,4]';     }
parameters{	         simplex[4] prop;                  }
model{               prop ~ dirichlet(alpha);  

fit= stan(model_code = stancode, cores=4, iter = 10000, warmup = 1000)

tidybayes::spread_draws(fit2, prop_soft[N]) %>% 
    select(N,prop_soft) %>% 
    arrange(N,prop_soft) %>%
    mutate(i = 1:n()) %>% 
    left_join(
        tidybayes::spread_draws(fit, prop[N]) %>% 
            select(N,prop) %>%
            arrange(N,prop) %>%
            mutate(i = 1:n()) 
    ) %>% 
    ggplot(aes(prop, prop_soft)) + 
    geom_point() + 
    facet_wrap(~N) + 
    geom_abline()

pairs softmax - no jacobian

pairs source model

Then, when I add the simple jacobian everything goes crazy.

[stemangiola]

Actually I can see a bit of curvature compared to the comparison of two sampling of the source simplex model.

However the curvature seems rather small.

[stemangiola]

Just a small study for highlighting the consequences of the absence of Jacobian correction. Summary: I notice that for the model stated above, where it really makes the difference is for K = 2. But maybe I am not getting some important nuances of the Jacobian correction.

For K = 2 (x-axis is the simplex from a native non transformed model)

For K = 3 (x-axis is the simplex from a native non transformed model)

For K = 4 (x-axis is the simplex from a native non transformed model)

However for K=3 we can see curvature if alpha = [1,1,1].

Anyway this was just a personal experiment that might be intersting for some.