So given a simple sinusoid-measured-noisily, one would think a straightforward model like this would be sufficient:
data{
int n ;
vector[n] y ;
vector[n] x ;
}
transformed data{
vector[n] y_scaled = (y-mean(y))/sd(y) ;
}
parameters{
real<lower=0> noise ;
real<lower=0> frequency ;
vector[2] phamp ; // phase & amplitude (but a transform thereof)
}
transformed parameters{
real amp = sqrt(dot_self(phamp));
real phase = atan2(phamp[1],phamp[2]);
vector[n] f = amp * sin(x*frequency - phase) ;
}
model{
noise ~ weibull(2,1) ; //peaked at ~.8, zero-at-zero, ~2% mass >2
amp ~ weibull(2,1) ; //ditto
target += log(amp) ; // jacobian for setting a prior on amp given it's derivation from phamp
// phase has an implied uniform prior
frequency ~ ... ; // prior on frequency should account for the range and spacing of x
y_scaled ~ normal(f,noise) ;
}
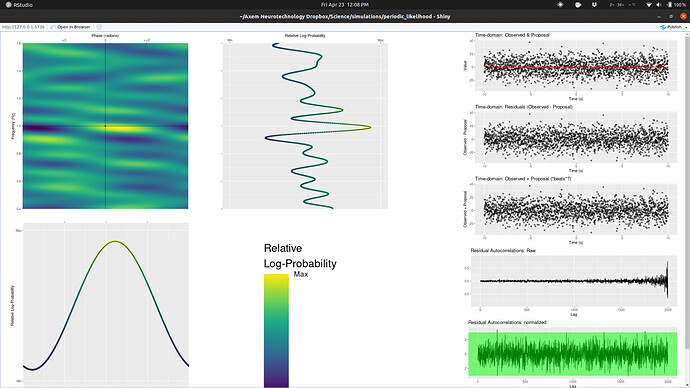
But it turns out that the likelihood topography (code to generate/explore here)
of even this simple model is massively multimodal:
in the frequency dimension in a confoundingly complex manner (i.e. it’s not just harmonics), causing typical multimodal sampling issues (different chains finding different modes).
I’ve cast a wide net in trying to find solutions to this, including bugging a bunch of astrophysics folks who I imagined must encounter this issue a ton, but so far as I can tell no one has developed any robust solutions to this (the astro folks seem to have contented themselves with simply doing a maximum-likelihoood search in a very constrained frequency range).
While it’s straightforward to reframe things as a Gaussian Process with a periodic kernel, this can be very compute-intensive (something I’d like to avoid as ultimately I’ll be looking to do inference in a realtime context), so I’ve been trying to come up with alternative solutions. I recently started learning about Hidden Markov Models, insipring a couple possible applications of HMMs to this periodic signals problem. My first thought was to model the derivative of the periodic signal as positive or negative, and that works to a degree, but felt pretty kludgey.
Then I realized that the derivative part is unnecessary (well, for sinusoids at least), leading me to think about the general structure whereby a periodic signal is modelled as an HMM with K states reflecting K ordered means with a transition matrix such that each state has a non-zero probability of transitioning to only it’s neighbors:
data{
int n ;
vector[n] y ; // assumed to be scaled with zero mean
int<lower=3> k ; //must be odd
}
transformed data{
int j = (k-1)/2 ; // num states on either side of the halfway state
}
parameters{
simplex[k] p0 ; // initial state probabilities
simplex[3] tp_arr[k-2] ; // transition probability for all but the most extreme
simplex[2] tp_ext[2] ; //transition probabilities for the extreme-most states
positive_ordered[j] m_pos ; // state means (should these maybe be simply equidistant?)
// positive_ordered[j] m_neg ; // for a sinusoid, can assume neg means same spacing as pos means
real<lower=0> noise ; //measurement noise
}
transformed parameters {
vector[k] m ;
m[j+1] = 0.0 ; // halfway state has 0 mean
for(i_j in 1:j){
// m[(j+1)-i_j] = -m_neg[i_j] ;
m[(j+1)-i_j] = -m_pos[i_j] ;
m[(j+1)+i_j] = m_pos[i_j] ;
}
matrix[k, k] tp_mat = rep_matrix(0,k,k) ;
for(i_k in 2:(k-1)){
tp_mat[i_k,(i_k-1):(i_k+1)] = tp_arr[i_k-1]' ;
}
tp_mat[1,1:2] = tp_ext[1]' ;
tp_mat[k,(k-1):k] = tp_ext[2]' ;
matrix[k, n] state_ll ;
for(i_n in 1:n) {
for(i_k in 1:k){
state_ll[i_k,i_n] = normal_lpdf(y[i_n]|m[i_k],noise) ;
}
}
}
model{
noise ~ std_normal() ;
m_pos ~ std_normal() ;
// m_neg ~ std_normal() ;
target += hmm_marginal(state_ll, tp_mat, p0) ;
}
generated quantities{
vector[n] fk ;
vector[n] fm ;
{
matrix[k,n] p = hmm_hidden_state_prob(state_ll, tp_mat, p0) ;
for(i_n in 1:n){
real highest_p = 0 ;
for(i_k in 1:k){
if(p[i_k,i_n]>highest_p){
highest_p = p[i_k,i_n] ;
fk[i_n] = i_k ;
fm[i_n] = m[i_k] ;
}
}
}
}
}
With this model, as K increases, we get more states that are closer together and thereby smoother and smoother realizations of data y. I’m thinking then that maybe there’s math that works out a representation for the limit of K=\infty, where I suspect the frequency of the true signal will determine the structure of the transition matrix, or whatever limit-level entity serves the role of the transition matrix.
But I’m super math-untrained, so thought I’d query the folks here on whether that’s possible. Thoughts anyone?
(One thing I’ll add as a post script: as expressed above, the sequential-K HMM only weakly implicates periodicity whereby each state should have an equal chance of proceeding to either of it’s neighbors. This “fits” periodic data where we pass through the state going both ways, but doesn’t fully reflect that the previous state determines the transition probabilities of the current state. But I guess that’s the fundamental nature/point of HMMs? And if I want to convey a transition that’s deterministic, I’m back in the function world of the first model above? I still wonder if some additional useful constraint might be achieved by, in addition to the HMM on the raw signal, also doing an HMM on the derivative, which I think would imply/induce the kind of transition directionality I’m thinking might be more periodic-accurate.)