testFrame <- data.frame(First=sample(1:10, 20, replace=T),
Second=sample(1:20, 20, replace=T), Third=sample(1:10, 20, replace=T),
Fourth=rep(c(“Alice”,“Bob”,“Charlie”,“David”), 5),
Fifth=rep(c(“Edward”,“Frank”,“Georgia”,“Hank”,“Isaac”),4))
basically I can go with:
1, model.matrix(~ 0+First + Second + Third + Fourth + Fifth, data=testFrame)
2, model.matrix(~ First + Second + Third + Fourth + Fifth, data=testFrame)
Since coxph does not have intercept, should I go with matrix 1? Or should I still feed the stan survival model with the most commonly used matrix 2?
Thank you for your advice in advance.
Hi, the answer really depends on how you code the Stan model so either one could be fine. Can you be clearer about your model?
1 Like
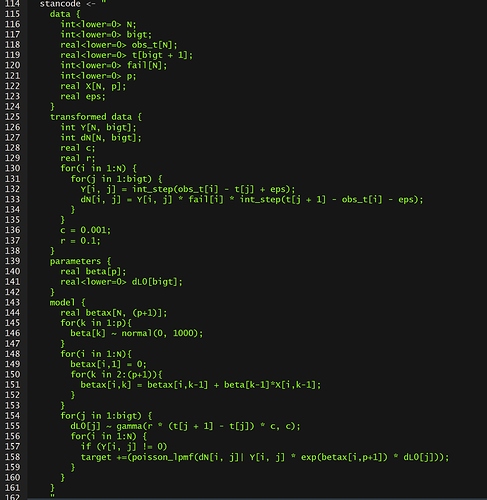
Thank you very much for your reply. Here is my model I learnt and modified from Leuk: Cox regression openbugs model.
http://www.openbugs.net/Examples/Leuk.html
See if you can identify a baseline hazard parameter in the Stan code. If not then your model matrix needs an intercept. The Cox model has an interesting interpretation but the piece you’re thinking about is just a regression for the log hazard
The stan code does have a baseline hazard modeled in. My question is even if I omit the intercept, design matrix one has one more factor than design matrix two, which one is proper in this case? In coxph, it has one less factor, i.e. use design matrix two but without intercept.
If you already have an intercept (log baseline hazard) then adding the intercept using the model matrix results in confounded parameters (log baseline hazard and intercept). So don’t do that one, it won’t work well.