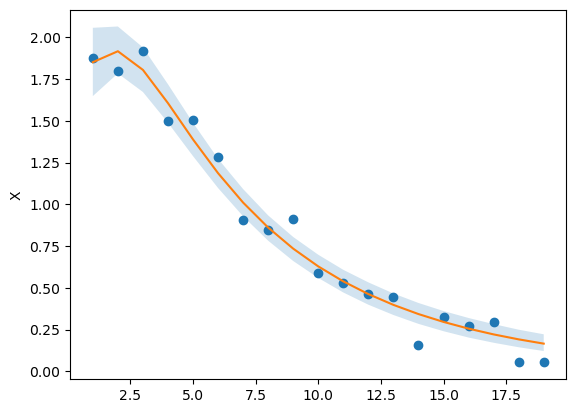
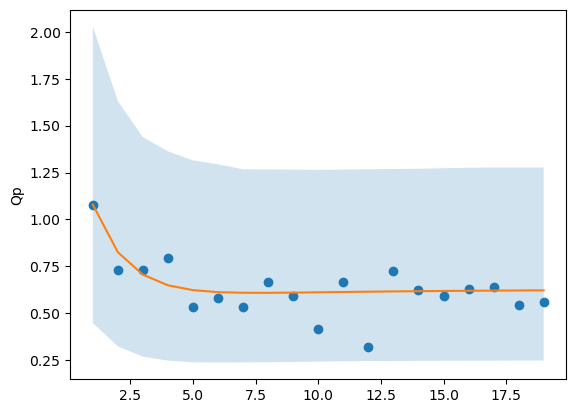
Hey @cgoold and @wds15, thanks for the help. I tried the lognormal distribution, it didn’t seem to help too much. I haven’t tried sundials, because that involves recompiling STAN, which I’m not sure I want to do just yet. Placing bounds on the parameters helped. Here’s what I’ve got:
#%%
import numpy as np
import pystan as pyst
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import pandas as pd
#%% Set up the parameters and initial conditions
rho = 0.7
Kp = 2
mu = 0.7
q0 = 0.3
d = 0.5
init = [5, 1, 2]
params = (rho, Kp, mu, q0, d)
t = np.arange(0, 20, 1)
t0 = t[0]
ts = t[1:]
#%% STAN SOLVER
droop_stan_s = """
functions{
real[] droop(real t,
real[] y,
real[] theta,
real[] x_r,
int[] x_i){
real dydt[3];
dydt[1] = 1*(1 - y[1]) - theta[1]*(y[1] / (theta[2] + y[1]))*y[3];
dydt[2] = theta[1]*(y[1] / (theta[2] + y[1])) - theta[3]*(y[2] - theta[4]);
dydt[3] = y[3]*theta[3]*(1 - theta[4]/y[2]) - theta[5]*y[3];
return dydt;
}
}
data{
int<lower=1> T;
real t0;
real ts[T];
real y0[3];
real theta[5];
}
transformed data{
real x_r[0];
int x_i[0];
}
transformed parameters{
}
generated quantities{
real yhat[T,3];
yhat = integrate_ode_rk45(droop, y0, t0, ts, theta, x_r, x_i);
}
"""
droop_comp_s = pyst.StanModel(model_code=droop_stan_s)
#%% Simulate data
solver_dict = {'T': len(ts), 't0': t0, 'ts': ts, 'y0': init, 'theta': params}
sim_data = droop_comp_s.sampling(data=solver_dict,
algorithm='Fixed_param',
iter=1, chains=1)
yhat = sim_data.extract('yhat')['yhat']
yhat_obs = yhat + np.random.normal(0, 0.1, yhat.shape)
plt.plot(ts, yhat[0,:,0], 'b-', yhat_obs[0,:,0], 'bo', label='P')
plt.plot(ts, yhat[0,:,1], 'r-', yhat_obs[0,:,1], 'ro', label='Qp')
plt.plot(ts, yhat[0,:,2], 'k-', yhat_obs[0,:,2], 'ko', label='X')
plt.legend()
plt.savefig('/home/nate/Desktop/data.png')
plt.show()

#%% STAN estimator
droop_stan_e = """
functions{
real[] droop(real t,
real[] y,
real[] theta,
real[] x_r,
int[] x_i){
real dydt[3];
dydt[1] = 1*(1 - y[1]) - theta[1]*(y[1] / (theta[2] + y[1]))*y[3];
dydt[2] = theta[1]*(y[1] / (theta[2] + y[1])) - theta[3]*(y[2] - theta[4]);
dydt[3] = y[3]*theta[3]*(1 - theta[4]/y[2]) - theta[5]*y[3];
return dydt;
}
}
data{
int<lower=1> T;
real y[T,3];
real t0;
real ts[T];
}
transformed data{
real x_r[0];
int x_i[0];
}
parameters{
real<lower=0> y0[3];
real<lower=0> rho;
real<lower=0> Kp;
real<lower=0> mu;
real<lower=0> q0;
real<lower=0, upper=1> d;
vector<lower=0>[3] sigma_y;
}
transformed parameters{
real yhat[T,3];
real theta[5];
theta[1] = rho;
theta[2] = Kp;
theta[3] = mu;
theta[4] = q0;
theta[5] = d;
yhat = integrate_ode_rk45(droop, y0, t0, ts, theta, x_r, x_i);
}
model{
for(t in 1:T){
y[t] ~ lognormal(log(yhat[t]), sigma_y);
}
sigma_y ~ lognormal(-1, 1);
y0 ~ normal(0,1);
rho ~ normal(0,1);
Kp ~ normal(0,1);
mu ~ normal(0,1);
q0 ~ normal(0,1);
d ~ normal(0,1);
}
generated quantities{
}
"""
droop_comp_e = pyst.StanModel(model_code=droop_stan_e)
#%%
estimate_dict = {'T': len(ts), 't0': t0, 'ts': ts, 'y': yhat_obs[0]}
droop_output = droop_comp_e.sampling(data=estimate_dict,
iter=1000, chains=4)
Gradient evaluation took 0.00069 seconds
1000 transitions using 10 leapfrog steps per transition would take 6.9 seconds.
Adjust your expectations accordingly!
Gradient evaluation took 0.000793 seconds
1000 transitions using 10 leapfrog steps per transition would take 7.93 seconds.
Adjust your expectations accordingly!
Gradient evaluation took 0.000711 seconds
1000 transitions using 10 leapfrog steps per transition would take 7.11 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 1000 [ 0%] (Warmup)
Gradient evaluation took 0.011008 seconds
1000 transitions using 10 leapfrog steps per transition would take 110.08 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 1000 [ 0%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: lognormal_lpdf: Location parameter[3] is nan, but must be finite! (in 'unknown file name' at line 48)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 100 / 1000 [ 10%] (Warmup)
Iteration: 200 / 1000 [ 20%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
Iteration: 300 / 1000 [ 30%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 400 / 1000 [ 40%] (Warmup)
Iteration: 100 / 1000 [ 10%] (Warmup)
Iteration: 500 / 1000 [ 50%] (Warmup)
Iteration: 501 / 1000 [ 50%] (Sampling)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 1 / 1000 [ 0%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: integrate_ode_rk45: parameter vector[3] is inf, but must be finite! (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 600 / 1000 [ 60%] (Sampling)
Iteration: 200 / 1000 [ 20%] (Warmup)
Iteration: 1 / 1000 [ 0%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: lognormal_lpdf: Location parameter[3] is -inf, but must be finite! (in 'unknown file name' at line 48)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 700 / 1000 [ 70%] (Sampling)
Iteration: 100 / 1000 [ 10%] (Warmup)
Iteration: 300 / 1000 [ 30%] (Warmup)
Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Exception: Max number of iterations exceeded (1000000). (in 'unknown file name' at line 43)
If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Iteration: 800 / 1000 [ 80%] (Sampling)
Iteration: 200 / 1000 [ 20%] (Warmup)
Iteration: 100 / 1000 [ 10%] (Warmup)
Iteration: 900 / 1000 [ 90%] (Sampling)
Iteration: 400 / 1000 [ 40%] (Warmup)
Iteration: 300 / 1000 [ 30%] (Warmup)
Iteration: 200 / 1000 [ 20%] (Warmup)
Iteration: 1000 / 1000 [100%] (Sampling)
Elapsed Time: 21.0428 seconds (Warm-up)
23.1567 seconds (Sampling)
44.1995 seconds (Total)
Iteration: 500 / 1000 [ 50%] (Warmup)
Iteration: 501 / 1000 [ 50%] (Sampling)
Iteration: 400 / 1000 [ 40%] (Warmup)
Iteration: 600 / 1000 [ 60%] (Sampling)
Iteration: 300 / 1000 [ 30%] (Warmup)
Iteration: 500 / 1000 [ 50%] (Warmup)
Iteration: 501 / 1000 [ 50%] (Sampling)
Iteration: 700 / 1000 [ 70%] (Sampling)
Iteration: 600 / 1000 [ 60%] (Sampling)
Iteration: 400 / 1000 [ 40%] (Warmup)
Iteration: 700 / 1000 [ 70%] (Sampling)
Iteration: 800 / 1000 [ 80%] (Sampling)
Iteration: 800 / 1000 [ 80%] (Sampling)
Iteration: 500 / 1000 [ 50%] (Warmup)
Iteration: 501 / 1000 [ 50%] (Sampling)
Iteration: 900 / 1000 [ 90%] (Sampling)
Iteration: 900 / 1000 [ 90%] (Sampling)
Iteration: 1000 / 1000 [100%] (Sampling)
Elapsed Time: 20.9352 seconds (Warm-up)
12.3998 seconds (Sampling)
33.335 seconds (Total)
Iteration: 1000 / 1000 [100%] (Sampling)
Elapsed Time: 44.4743 seconds (Warm-up)
17.4008 seconds (Sampling)
61.875 seconds (Total)
Iteration: 600 / 1000 [ 60%] (Sampling)
Iteration: 700 / 1000 [ 70%] (Sampling)
Iteration: 800 / 1000 [ 80%] (Sampling)
Iteration: 900 / 1000 [ 90%] (Sampling)
Iteration: 1000 / 1000 [100%] (Sampling)
Elapsed Time: 34.9841 seconds (Warm-up)
18.2123 seconds (Sampling)
53.1963 seconds (Total)
droop_output.plot()
#%%
theta = pd.DataFrame(droop_output.extract('theta')['theta'],
columns = ('rho', 'Kp', 'mu', 'q0', 'd'))
plt.errorbar(params, theta.mean(), yerr=theta.std(), fmt='o')
plt.plot([0,2], [0,2], 'k:')
plt.savefig('/home/nate/Desktop/params.png')
plt.close()

y0 = pd.DataFrame(droop_output.extract('y0')['y0'],
columns=['P', 'Qp', 'X'])
plt.errorbar(init, y0.mean(), yerr=y0.std(), fmt='o')
plt.plot([0,5], [0,5], 'k:')
plt.savefig('/home/nate/Desktop/inits.png')
plt.close()

The process still seems to be slow, taking about a minute to run 1000 iterations. Is that just normal for ODE solvers because the numerical solver itself is slow?
Also, any suggestion for helping estimate Kp? The half saturation constant is the only parameter that appears to be consistently underestimated in the model (though it is usually not all that biologically interesting, anyway).
All of this is building up to another question, which is how to accurately estimate the values of a compartment when data are only available for some of the compartments (as in, how can I accurately estimate the parameters as well as Qp when I only have data for X and P, but that’s a different question).