Hi,
I’m currently working on an occupancy model where I am modeling the number of detections with a Poisson detection model instead of a binary detection model. Roughly, for site i \in \{ 1, 2, \dots, \textrm{n_site} \}, z_i \sim \textrm{Bernoulli} ( \psi), where \psi is the occupancy probability and for survey j \in \{ 1, 2, \dots, \textrm{n_survey} \}, the detection history is modeled as y_{ij} \sim \textrm{Poisson} ( z_i \times \lambda_{ij}), where y_{ij} is a positive integer or 0 and \lambda_{ij} are the site-and-survey specific detection rates. Of course, to fit this model in Stan the discrete occupancy states z_i are marginalised out.
The full model is a bit more complicated than this, as sites are nested within regions. For the occupancy probabilities, I am modeling the region-specific occupancy probabilities with a Gaussian random effect on the log odds of \psi. I’m also interested in temporal and spatial variation in \lambda_{ij}. This model runs quite well without many divergent transitions (<1%) and posterior predictions match the observed data well.
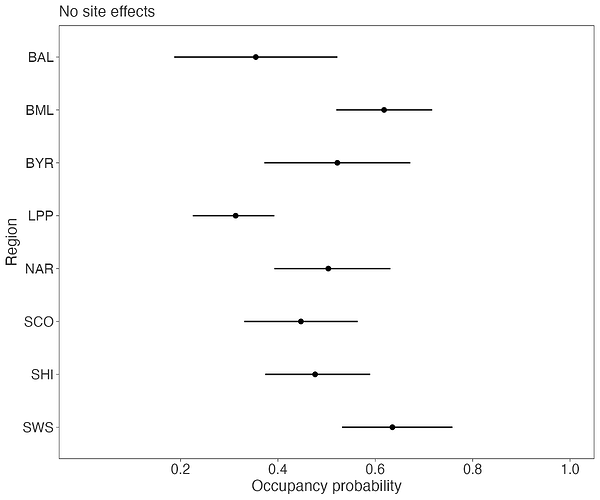
Now, something interesting happens with the occupancy probabilities when I model the log detection rates with site-specific random effects through a Gaussian process. First, if I completely ignore site-level variation in the detection rates, my region-specific occupancy probabilities look like this:
When I add noncentered site-level Gaussian random effects (with region-level standard deviations log_lambda_spat_s[r]) to the log detection rate like so:
\\ ...
for (r in 1:n_region) {
vector[n_site[r]] log_lambda_spat = log_lambda_spat_s[r] * log_lambda_z[1:n_site[r], r];
}
\\ ...
My region-specific occupancy probabilities look similar and sensible:
However, when I add noncentered site-level random effects through a Gaussian process using the sites-specific UTM coordinates like this, where log_lambda_spat_s[r] are the region-specific marginal SDs and log_lambda_spat_l[r] are region-specific length-scales with inverse Gamma priors:
\\ ...
for (r in 1:n_region) {
log_lambda_spat = cholesky_decompose(add_diag(
gp_exp_quad_cov(utm[r, 1:n_site[r]], log_lambda_spat_s[r], log_lambda_spat_l[r]),
1e-9))
* log_lambda_z[1:n_site[r], r];
}
\\ ...
There is a big impact on my occupancy probabilities:
So, it appears that incorporating spatial site-level variation through a Gaussian process has a big influence on my occupancy probabilities and they look totally different than when the site-level variation is just modeled as Gaussian random effects. I don’t think I’ve really mis-specified anything, but I’ll add the full model code below just in case. However, I definitely seem to have the problem isolated to the addition of spatial random effects as opposed to just Gaussian random effects.
Is this expected behaviour of a GP, or is there something obviously causing this? I realise it’s not that much of a Stan-specific issue, but I couldn’t think of where else to pose the question.
Model code:
functions {
/**
* Log probability of partial sum over regions of continuous-time occupancy model
*
* @param seq_region Sequence of regions from 1 to n_region
* @param start Start of seq_region for partial sum
* @param end End of seq_region for partial sum
* @param y Detection history
* @param q Number of detections per site
* @param n_site Number of sites per region
* @param n_survey_max Maximum number of possible "surveys" (night hours) in detection history
* @param n_survey Number of "surveys" (night hours) per site
* @param n_date Number of dates in detection history
* @param n_hour Maximum number of hours per night
* @param log_tau Log time of "survey" expressed as log number of hours per "survey" per site
* @param surveys Indices of "surveys" conducted per site
* @param utm UTM coordinates per site
* @param logit_psi_a Log odds occupancy intercept
* @param logit_psi_region Region effects on log odds occupancy
* @param log_lambda_a Log hourly detection (call) rate intercept
* @param log_lambda_region Region effects on log hourly detection (call) rate
* @param log_lambda_spat_s Marginal SDs of spatial Gaussian process (GP) on log hourly detection (call) rate per region
* @param log_lambda_spat_l Length scales of spatial GP on log hourly detection (call) rate per region
* @param log_lambda_spat_l_prior Inverse gamma shape and scale parameters for length scales of spatial GP per region
* @param log_lambda_z z-scores of sites for spatial GPs
* @param log_lambda_date Date-level multivariate GP realisations per date and region
* @param log_lambda_hour Hour-level multivariate GP realisations per hour and region
* @param nb Binary indicating whether calls are modeled with negative binomial (nb = 1) or Poisson (nb = 0) distribution
* @param alpha Flexibility parameters of negative binomial distribution per region
*
* @return Log probability for subset of regions
*/
real partial_sum_lpmf(
data array[] int seq_region, data int start, data int end,
data array[,,] int y, data array[,] int q, data array[] int n_site, int n_survey_max, data array[,] int n_survey,
data int n_date, data int n_hour, data array[] matrix log_tau, data array[,,] int surveys, data array[,] vector utm,
real logit_psi_a, vector logit_psi_region, real log_lambda_a, vector log_lambda_region,
vector log_lambda_spat_s, vector log_lambda_spat_l, matrix log_lambda_spat_l_prior, matrix log_lambda_z,
matrix log_lambda_date, matrix log_lambda_hour,
data int nb, vector alpha) {
// initialise partial target
real ptarget = 0;
for (r in start:end) {
// initialise occupancy probabilities and hourly call rates and spatial GP
vector[n_site[r]] psi, log_psi, log1m_psi, log_lambda_spat;
matrix[n_survey_max, n_site[r]] log_lambda;
// occupancy probabilities
psi = rep_vector(inv_logit(logit_psi_a + logit_psi_region[r]), n_site[r]);
log_psi = log(psi);
log1m_psi = log1m(psi);
// spatial GP of call rates
ptarget += exponential_lupdf(log_lambda_spat_s[r] | 1);
ptarget += inv_gamma_lupdf(log_lambda_spat_l[r] | log_lambda_spat_l_prior[1, r], log_lambda_spat_l_prior[2, r]);
ptarget += std_normal_lupdf(log_lambda_z[1:n_site[r], r]);
log_lambda_spat = log_lambda_spat_s[r] * log_lambda_z[1:n_site[r], r]; // Gaussian effects
// log_lambda_spat = cholesky_decompose(add_diag(gp_exp_quad_cov(utm[r, 1:n_site[r]], log_lambda_spat_s[r], log_lambda_spat_l[r]), 1e-9)) * log_lambda_z[1:n_site[r], r]; // GP effects
// hourly call rates
log_lambda = rep_matrix(log_lambda_a + log_lambda_region[r], n_survey_max, n_site[r]);
log_lambda += rep_matrix(log_lambda_spat, n_survey_max)';
log_lambda += rep_matrix(to_vector(rep_matrix(log_lambda_date[:, r], n_hour)') + to_vector(rep_matrix(log_lambda_hour[:, r], n_date)), n_site[r]);
log_lambda += log_tau[r][:, 1:n_site[r]];
// flexibility parameter of negative binomial
ptarget += pc_nb_lupdf(alpha[r] | 1);
real phi = 1 / alpha[r];
// likelihood
for (s in 1:n_site[r]) {
if (nb) {
if (q[r, s] > 0) {
ptarget += log_psi[s] + neg_binomial_2_log_lupmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s], phi);
} else {
ptarget += log_sum_exp(log_psi[s] + neg_binomial_2_log_lupmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s], phi), log1m_psi[s]);
}
} else {
if (q[r, s] > 0) {
ptarget += log_psi[s] + poisson_log_lupmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s]);
} else {
ptarget += log_sum_exp(log_psi[s] + poisson_log_lupmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s]), log1m_psi[s]);
}
}
} // s
} // r
return ptarget;
}
/**
* Return a vector of gamma prior parameters where the probability mass is contained
* within pre-specified lower and upper bounds, using Stan's algebraic solver. See
* https://betanalpha.github.io/assets/case_studies/some_containment_prior_models.html
*
* @param params_guess Best guess of the shape and scale for the solver to start
* @param theta Lower and upper bounds of input
* @param tails Lower and upper bounds of probability mass
* @param x_i Integer array (must be included even if empty)
*
* @return Vector of inverse gamma shapes
*/
vector inv_gamma_prior(vector guess, vector theta, array[] real tails, array[] int x_i) {
vector[2] params;
params[1] = inv_gamma_cdf(theta[1] | guess[1], guess[2]) - tails[1];
params[2] = inv_gamma_cdf(theta[2] | guess[1], guess[2]) - tails[2];
return params;
}
/**
* Log of the density of the approximate penalised complexity (PC) prior for the flexibility parameter,
* parameterised as alpha = 1 / phi, of the negative binomial distribution.
* See: https://dansblog.netlify.app/posts/2022-08-29-priors4/priors4
*
* @param lambda Scaling parameter
* @param alpha Flexibility parameter of the negative binomial distribution
*
* @return Log probability density, dropping constant additive terms
*/
real pc_nb_lpdf(real alpha, real lambda) {
real sqrt_alpha = sqrt(alpha);
return log(lambda) - log(sqrt_alpha) - lambda * sqrt_alpha;
}
// get number of correlation from the number of dimensions
int n_cor(int n_dim) {
return n_dim * (n_dim - 1) / 2;
}
/**
* Vector of correlations from lower triangular Cholesky factor of correlation matrix
*
* @param Omega_L Lower triangular Cholesky factor of correlation matrix
*
* @return Vector of correlations
*/
// get vector of correlations from lower triangular Cholesky factor of correlation matrix
vector cors(matrix Omega_L) {
int n_dim = rows(Omega_L);
int n_rho = n_cor(n_dim);
vector[n_rho] rho;
matrix[n_dim, n_dim] Omega = multiply_lower_tri_self_transpose(Omega_L);
int r = 1;
for (k in 1:(n_dim - 1)) {
for (kk in (k + 1):n_dim) {
rho[r] = Omega[k, kk];
r = r + 1;
}
}
return rho;
}
}
data {
int n_region, n_site_max, n_survey_max, n_date, n_hour, grainsize, nb;
array[n_region] int<lower=1> n_site;
array[n_region, n_site_max] int n_survey;
array[n_region] matrix[n_site_max, n_survey_max] tau;
array[n_region, n_site_max, n_survey_max] int surveys, y;
array[n_region, n_site_max] vector[2] utm;
matrix<lower=0>[n_region, 2] dist;
}
transformed data {
array[n_region] matrix[n_survey_max, n_site_max] log_tau;
array[n_region, n_site_max] int q;
for (r in 1:n_region) {
log_tau[r] = log(tau[r])';
for (s in 1:n_site[r]) {
q[r, s] = sum(y[r, s, surveys[r, s, 1:n_survey[r, s]]]);
}
}
array[n_region] int seq_region = linspaced_int_array(n_region, 1, n_region);
array[n_date] real dates = linspaced_array(n_date, 1, n_date);
array[n_hour] real hours = linspaced_array(n_hour, 1, n_hour);
array[2] real tails = { 0.01, 0.99 };
array[0] int x_i;
matrix[2, n_region] log_lambda_spat_l_prior;
for (r in 1:n_region) {
log_lambda_spat_l_prior[:, r] = algebra_solver_newton(inv_gamma_prior, [1, 1]', dist[r]', tails, x_i);
}
matrix[2, 2] theta = [ [1, 1], [n_date, n_hour] ];
matrix[2, 2] log_lambda_temp_l_prior;
for (i in 1:2) {
log_lambda_temp_l_prior[:, i] = algebra_solver_newton(inv_gamma_prior, [1, 1]', theta[:, i], tails, x_i);
}
print("log_lambda_spat_l_prior: ", log_lambda_spat_l_prior);
print("log_lambda_temp_l_prior: ", log_lambda_temp_l_prior);
}
parameters {
real<lower=0, upper=1> psi_a;
real<lower=0> logit_psi_t;
vector[n_region] logit_psi_z;
real<lower=0> lambda_a;
real<lower=0> log_lambda_t;
// real log_lambda_spat_s_m;
// real<lower=0> log_lambda_spat_s_t;
vector<lower=0>[n_region] log_lambda_spat_s, log_lambda_spat_l;
matrix<lower=0>[n_region, 2] log_lambda_temp_s;
vector<lower=0>[2] log_lambda_temp_l;
array[2] cholesky_factor_corr[n_region] log_lambda_temp_O_L;
tuple(vector[n_region], vector[n_region], matrix[n_site_max, n_region], matrix[n_date, n_region], matrix[n_hour, n_region]) log_lambda_z;
vector<lower=0>[n_region] alpha;
}
transformed parameters {
real logit_psi_a = logit(psi_a);
vector[n_region] logit_psi_region = logit_psi_t * logit_psi_z;
real log_lambda_a = log(lambda_a);
vector[n_region] log_lambda_region = log_lambda_t * log_lambda_z.1;
// vector[n_region] log_lambda_spat_s = exp(log_lambda_spat_s_m + log_lambda_spat_s_t * log_lambda_z.2);
matrix[n_date, n_region] log_lambda_date = cholesky_decompose(add_diag(gp_exp_quad_cov(dates, 1, log_lambda_temp_l[1]), 1e-9)) * log_lambda_z.4 * diag_pre_multiply(log_lambda_temp_s[:, 1], log_lambda_temp_O_L[1])';
matrix[n_hour, n_region] log_lambda_hour = cholesky_decompose(add_diag(gp_exp_quad_cov(hours, 1, log_lambda_temp_l[2]), 1e-9)) * log_lambda_z.5 * diag_pre_multiply(log_lambda_temp_s[:, 2], log_lambda_temp_O_L[2])';
}
model {
// occupancy priors
target += beta_lupdf(psi_a | 1, 1);
target += exponential_lupdf(logit_psi_t | 1);
target += std_normal_lupdf(logit_psi_z);
// detection priors
target += exponential_lupdf(lambda_a | 1);
target += exponential_lupdf(log_lambda_t | 1);
// target += std_normal_lupdf(log_lambda_spat_s_m);
// target += exponential_lupdf(log_lambda_spat_s_t | 1);
target += exponential_lupdf(to_vector(log_lambda_temp_s) | 1);
for (i in 1:2) {
target += inv_gamma_lupdf(log_lambda_temp_l[i] | log_lambda_temp_l_prior[1, i], log_lambda_temp_l_prior[2, i]);
target += lkj_corr_cholesky_lpdf(log_lambda_temp_O_L[i] | 2);
}
target += std_normal_lupdf(log_lambda_z.1);
target += std_normal_lupdf(log_lambda_z.2);
target += std_normal_lupdf(to_vector(log_lambda_z.4));
target += std_normal_lupdf(to_vector(log_lambda_z.5));
// likelihood
target += reduce_sum(partial_sum_lupmf, seq_region, grainsize,
y, q, n_site, n_survey_max, n_survey,
n_date, n_hour, log_tau, surveys, utm,
logit_psi_a, logit_psi_region, log_lambda_a, log_lambda_region,
log_lambda_spat_s, log_lambda_spat_l, log_lambda_spat_l_prior, log_lambda_z.3,
log_lambda_date, log_lambda_hour,
nb, alpha);
}
generated quantities {
array[2] vector[n_cor(n_region)] log_lambda_temp_rho;
for (i in 1:2) {
log_lambda_temp_rho[i] = cors(log_lambda_temp_O_L[i]);
}
matrix[n_site_max, n_region] log_lambda_spat = rep_matrix(0, n_site_max, n_region);
vector[sum(n_site)] log_lik = rep_vector(0, sum(n_site));
{
for (r in 1:n_region) {
vector[n_site[r]] psi, log_psi, log1m_psi;
matrix[n_survey_max, n_site[r]] log_lambda;
psi = rep_vector(inv_logit(logit_psi_a + logit_psi_region[r]), n_site[r]);
log_psi = log(psi);
log1m_psi = log1m(psi);
// log_lambda_spat[1:n_site[r], r] = cholesky_decompose(add_diag(gp_exp_quad_cov(utm[r, 1:n_site[r]], log_lambda_spat_s[r], log_lambda_spat_l[r]), 1e-9)) * log_lambda_z.3[1:n_site[r], r];
log_lambda_spat[1:n_site[r], r] = log_lambda_spat_s[r] * log_lambda_z.3[1:n_site[r], r];
log_lambda = rep_matrix(rep_vector(log_lambda_a + log_lambda_region[r], n_survey_max), n_site[r]);
log_lambda += rep_matrix(log_lambda_spat[1:n_site[r], r], n_survey_max)';
log_lambda += rep_matrix(to_vector(rep_matrix(log_lambda_date[:, r], n_hour)') + to_vector(rep_matrix(log_lambda_hour[:, r], n_date)), n_site[r]);
log_lambda += log_tau[r][:, 1:n_site[r]];
real phi = 1 / alpha[r];
for (s in 1:n_site[r]) {
int i = sum(n_site[1:r]) - n_site[r] + s;
if (nb) {
if (q[r, s] > 0) {
log_lik[i] += log_psi[s] + neg_binomial_2_log_lpmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s], phi);
} else {
log_lik[i] += log_sum_exp(log_psi[s] + neg_binomial_2_log_lpmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s], phi), log1m_psi[s]);
}
} else {
if (q[r, s] > 0) {
log_lik[i] += log_psi[s] + poisson_log_lpmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s]);
} else {
log_lik[i] += log_sum_exp(log_psi[s] + poisson_log_lpmf(y[r, s, surveys[r, s, 1:n_survey[r, s]]] | log_lambda[surveys[r, s, 1:n_survey[r, s]], s]), log1m_psi[s]);
}
}
}
}
}
}
Thanks!
Matt