Fixing my multilevel model to avoid non physical results from the posterior prediction

Interfaces brms
1

Hello. I’m playing with brms trying to fit a multilevel model to rheological data, and I’m getting results for model prediction with no physical meaning. I’m here trying to get help in how to set up my model to avoid this problem. My background in statistics is lackluster, so pardon me if I make some mistake while writing this post.

Background: I have a very large database of lab measurements of the flow behaviour of a clay suspension, which behaves as a non newtonian fluid. Using a rotational rheometer, we force the sample through different shear rates, and record the applied shear stress on the fluid, through 4 different loading “phases”. We hypothesize that the fluid behaviour is dependant on the solids content of the sample and on the the test “phase”. The acquired database is as follows:

> head(dat_teste)
  sample   phase  SC   gamma   tau
1 A020102      2  60  70.030  3164
2 A020102      2  60  38.490  2810
3 A020102      2  60  20.480  2522
4 A020102      2  60  10.880  2292
5 A020102      2  60   5.796  2148
6 A020102      2  60   3.085  2028

In which ‘phase’ is the test phase (numeric, integer, categorized), ‘SC’ is the solids content (numeric, integer, categorized), ‘gamma’ is the recorded shear rate (numeric), and ‘tau’ is the recorded shear stress (numeric). There are two different values for ‘phase’ and three different values for ‘SC’ in the small part of the database I’m using as test.

The data, for a given sample, should follow the Herschel-Bulkley model:
\tau=a+b \gamma ^c
With a, b and c as the model parameters.

Model construction in brms: I’m following Granville Matheson’s brms nonlinear modelling syntax guide, which I could adapt with relative success. I set up my model as follows:

model_HB <- brms::bf(tau ~ a + b * (gamma^c),
                     a ~ 1 + (1|SC) + (1|SC:phase),
                     b ~ 1 + (1|SC) + (1|SC:phase),
                     c ~ 1 + (1|SC) + (1|SC:phase),
                     nl = TRUE)

prior <- c(prior(uniform(10, 5000), nlpar = 'a', lb = 10, ub = 5000),
           prior(uniform(1, 1000), nlpar = 'b', lb = 1, ub = 1000),
           prior(uniform(10^-3, 1), nlpar = 'c', lb = 10^-3, ub = 1))

fit1 <- brm(formula = model_HB ,
             data = dat_test,
             family = brmsfamily('Gaussian'),
             prior = prior,
             control = list(adapt_delta = 0.9),
             iter = 10000,
             warmup = 5000,
             thin = 5,
             chains = 4,
             seed = 123)

The fit appears to have run with no problems.

> summary(fit2)
Group-Level Effects: 
~SC (Number of levels: 3) 
                Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(a_Intercept)   643.46    337.97   228.17  1523.17 1.00     3726     3434
sd(b_Intercept)    63.67     79.45     1.70   292.74 1.00     3619     3865
sd(c_Intercept)     0.23      0.29     0.01     1.01 1.00     3527     3937

~SC:phase (Number of levels: 6) 
                Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(a_Intercept)   146.06    125.44    29.41   503.74 1.00     3520     3360
sd(b_Intercept)    35.06     31.49     1.80   118.06 1.00     3637     3643
sd(c_Intercept)     0.07      0.08     0.00     0.28 1.00     3713     3703

Population-Level Effects: 
            Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
a_Intercept   872.30    378.63   188.42  1719.29 1.00     3640     3363
b_Intercept    92.10     50.44    17.71   222.20 1.00     3623     3702
c_Intercept     0.49      0.15     0.15     0.82 1.00     3952     3774

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma   557.86      7.16   543.97   572.04 1.00     4081     3929

However, when investigating results, I came across this problem: when computing intervals from the posterior predictive distribution, I get negative values for ‘tau’, which have no physical meaning in this case.

> predictive_interval(fit2)
                   5%      95%
...
 [123,]  269.22861269 2101.801
 [124,]  164.59882127 1972.046
 [125,]   68.15528121 1889.180
 [126,]    7.18404354 1826.386
 [127,]  -45.07619383 1788.156
 [128,]  -76.17254151 1747.468
 [129,] -104.48853666 1745.090
 [130,] -121.93558750 1728.839
 [131,] -149.53286987 1693.427
 [132,] -120.25919652 1664.096

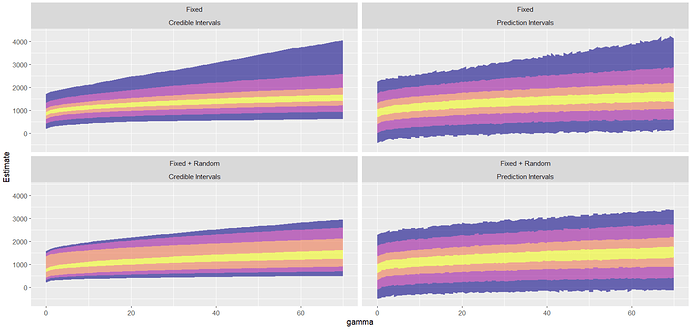
Following Matheson’s guide, I plotted this graph, which also shows this problem for the prediction intervals (obtained using the predict() function). Credible intervals (obtained using the fitted() function) seem fine.

Sem título
Sem título1472×703 71.7 KB

Can anyone please help me in figuring out how to fix this?
Any help is deeply appreciated.

  • R version 4.3.1
  • brms version 2.20.4
2

Welcome, @Fonseps, and thank you for providing such a clear explanation of your issue.

The short answer is that you are getting negative values of \tau in your intervals because (1) there is nothing structural in your model to prevent values of \tau < 0 and (2) the uncertainties in sd(SC) and sd(SC:phase) are so large that the values of a, b, and c in your posterior samples will sometimes be negative.

Let me unpack that more to show how this happens and what you might try to address the behavior.

(1) Choose a positive continuous response variable instead of the unbounded Gaussian.

Since \tau cannot be negative, you could consider changing the response distribution to one of the positive continuous distributions supported by Stan. Not knowing this area, I can’t offer good advice on which would be appropriate for the distribution of errors around \tau. If you go this route, be very mindful of the link function—you may need to transform the RHS of the H-B model.

(2) Add more informative priors to your group-level effects.

Look at the posterior medians (i.e., the Estimate column) for the two group-level sd(a_intercept) terms and the population level a_intercept in your model summary:

Compared to the population-level intercept, the group-level standard deviations are very large and will cause posterior samples of the a term that enters the H-B model to include negative values. We can see this if, for simplicity, we plug the posterior medians into

The implied distribution of the a parameter will include negative values, some of which are very large.

n <- 1e5
a <- 872.30 +  # a_intercept
  rnorm(n, mean = 0, sd = 643.46) + # ~SC sd(a_intercept)
  rnorm(n, mean = 0, sd = 146.06) # ~SC:phase sd(a_intercept)
hist(a)

image
image1052×786 11.4 KB

Maybe this is consistent with the physical interpretation of a, but I suspect it’s not given the bounds you set on the population-level intercept. Same goes for the other non-linear parameters b and c.

As a general practice, most Stan users will recommend using more informed priors rather than (un)bounded uniform distributions. Prior predictive checks are a good tool to help identify priors that are consistent with physical reality, and a number of guides are available (here here here).

Finally, and perhaps most beyond my depth, it’s not immediately clear from your data preview why you are modeling solid content (SC) as a group-level effect. If this is a categorical predictor and it’s reasonable to assume that the effects of group 60 are drawn from the same distribution as the other groups, then you can ignore this. However, it looks like the tutorial you are referencing doesn’t show any examples of population-level predictors for non-linear parameters. If SC is a continuous measure, you could modify the lines in your bf(...) call like so to treat it as a population-level slope:
a ~ 1 + SC + (1|phase)
Or, if you want to add group-level slopes for SC by phase:
a ~ 1 + SC + (1 + SC|phase)
And so on for the other non-linear parameters b and c. The language you use about phase makes it sound more like a group-level term, but generally speaking there’s no requirement that there be group-level effects in the non-linear parameter formulas.

I hope this helps, or at least gets you moving in the direction of a solution.

4 Likes