I first noticed this in real data, and finally have a fairly minimal reproducible example, as well as a fix, so I thought I’d post for folks to see and provide feedback. It would not surprise me if either I’ve made a mistake or if this is a known pathology. Attaching two models and R code here:
mvn_reliability.R (19.7 KB)
mvn.stan (1.7 KB)
pairwise.stan (2.7 KB)
(for the R code to work, put the stan files in a folder named stan_code)
The context is models using ~ multi_normal (and the cholesky and non-centered variants thereof) to express that multiple parameters/observables have the possibility of relationship.
Take for example multiple “things” I’ll call coefs (bc I originally observed this in a hierarchical model, and lazily didn’t rename things for this non-hierarchical minimal example), each observed from multiple human subjects. So it could be things like height, weight, income, etc, measured once for each subject. To model the relationships among the coefs, it’s common to just use a multivariate normal, with Stan code being:
data{
// num_subj: number of subj
int<lower=1> num_subj ;
// num_coef: number of coefficients modelled as intercorrelated
int<lower=1> num_coef ;
// subj_coef_array: array of values for each subj & coef
vector[num_coef] subj_coef_array[num_subj] ;
// num_cors: number of correlations implied by the number of coefficients; user-supplied bc Stan is strict in not permitting conversion from real to int.
// Must be: ((num_coef^2)-num_coef)/2
int num_cors ;
}
parameters{
// mean_coef: mean (across subj) for each coefficient
vector[num_coef] mean_coef ;
// sd_coef: sd (across subj) for each coefficient
vector<lower=0>[num_coef] sd_coef ;
// chol_corr: population-level correlations (on cholesky factor scale) amongst within-subject predictors
cholesky_factor_corr[num_coef] chol_corr ;
}
model{
////
// Priors
////
// normal(0,1) priors on all means
mean_coef ~ std_normal() ;
// weibull(2,1) priors on all sds (peaked at ~.8)
sd_coef ~ weibull(2,1) ;
// flat prior across sets of correlation matrices
chol_corr ~ lkj_corr_cholesky(1) ;
////
// Likelihood
////
// subj_coef_array as multivariate normal
subj_coef_array ~ multi_normal_cholesky(
rep_array(mean_coef,num_subj)
, diag_pre_multiply(sd_coef,chol_corr)
) ;
}
generated quantities{
// cor_vec: the lower-tri of the correlation matrix, flattened to a vector for efficient storage
vector[num_cors] cor_vec ;
{ // local env to avoid saving `cor`
matrix[num_coef,num_coef] cor = multiply_lower_tri_self_transpose(chol_corr) ;
int k = 0 ;
// extract lower-tri in column-major order
for(this_cor_col in 1:(num_coef-1)){
for(this_cor_row in (this_cor_col+1):num_coef){
k += 1 ;
cor_vec[k] = cor[this_cor_row,this_cor_col] ;
}
}
}
}
Generating data for this scenario where there are 100 subjects and 32 coefs, but all have zero true correlations, this model seems to be well-calibrated. The following plot shows a representation of the posterior for each of the (32*32-32)/2=496unique correlations, where they are stacked vertically with a colored bar showing the posterior interquartile range. The color of the bar indicates whether that correlation’s posterior 80% quantile interval includes the true value of zero (blue) or not (pink); we’d expect about 20% of the 80% intervals to exclude the true value, and that’s about what we get:
In fact, looking at the 50% and 80% calibrations quantitatively, they’re both a bit high:
> #coverage of 50% intervals
> binom.test(
+ x = sum(odd_mvn_cor_vec_info$fifty_covers_true)
+ , n = nrow(odd_mvn_cor_vec_info)
+ , p = .5
+ )
Exact binomial test
data: sum(odd_mvn_cor_vec_info$fifty_covers_true) and nrow(odd_mvn_cor_vec_info)
number of successes = 275, number of trials = 496, p-value = 0.01724
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5094720 0.5987465
sample estimates:
probability of success
0.5544355
> #coverage of 80% intervals
> binom.test(
+ x = sum(odd_mvn_cor_vec_info$eighty_covers_true)
+ , n = nrow(odd_mvn_cor_vec_info)
+ , p = .8
+ )
Exact binomial test
data: sum(odd_mvn_cor_vec_info$eighty_covers_true) and nrow(odd_mvn_cor_vec_info)
number of successes = 431, number of trials = 496, p-value =
6.483e-05
alternative hypothesis: true probability of success is not equal to 0.8
95 percent confidence interval:
0.8360367 0.8973839
sample estimates:
probability of success
0.8689516
A little weird, but let’s continue (though note this latter bit I only noticed while writing this up, so this may signal a bug that might in turn explain the below as well!).
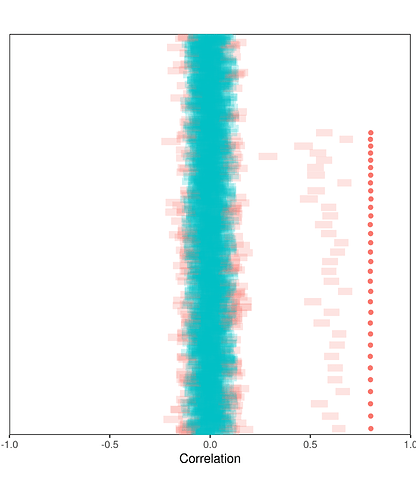
What if only most of the true correlations are all zero, but some are quite large? Here’s the same calibration plot for this mostly-zero-but-some-large scenario, this time with dots showing the true value of the non-zero correlations:
It’s clear that all of the non-zero correlations are dramatically under-estimated!
An alternative model that uses the same data declarations, is:
data{
// num_subj: number of subj
int<lower=1> num_subj ;
// num_coef: number of coefficients modelled as intercorrelated
int<lower=1> num_coef ;
// subj_coef_array: array of values for each subj & coef
vector[num_coef] subj_coef_array[num_subj] ;
// num_cors: number of correlations implied by the number of coefficients; user-supplied bc Stan is
// strict in not permitting conversion from real to int.
// Must be: ((num_coef^2)-num_coef)/2
int num_cors ;
}
transformed data{
// subj_coef_mat: just a reformat of subj_coef_array for convenience
matrix[num_subj,num_coef] subj_coef_mat ;
for(this_subj in 1:num_subj){
subj_coef_mat[this_subj] = transpose(subj_coef_array[this_subj]) ;
}
// corz_se: standard error for correlations on Fisher's Z scale
real corz_se = 1/sqrt(num_subj-3) ;
// obs_z: observed correlations, on Fisher's Z scale
vector[num_cors] obs_z ;
{
int k = 0 ;
vector[num_cors] obs_r ;
// looping over lower-tri to compute correlation between each column in subj_coef
for(this_coef in 1:(num_coef-1)){
for(this_other_coef in (this_coef+1):num_coef){
k += 1 ;
obs_r[k] = (
sum(
( subj_coef_mat[,this_coef] - mean(subj_coef_mat[,this_coef]) )
.* ( subj_coef_mat[,this_other_coef] - mean(subj_coef_mat[,this_other_coef]) )
)
) / (
(num_subj-1) * sd(subj_coef_mat[,this_coef]) * sd(subj_coef_mat[,this_other_coef])
) ;
}
}
obs_z = atanh(obs_r) ;
}
}
parameters{
// mean_coef: mean (across subj) for each coefficient
vector[num_coef] mean_coef ;
// sd_coef: sd (across subj) for each coefficient
vector<lower=0>[num_coef] sd_coef ;
// corz_vec: population-level correlations (on Fisher's-Z scale) among within-subject predictors
vector[num_cors] corz_vec ;
}
model{
////
// Priors
////
// normal(0,1) priors on all means
mean_coef ~ std_normal() ;
// weibull(2,1) priors on all sds (peaked at ~.8)
sd_coef ~ weibull(2,1) ;
// normal(0,.74) priors on all corz
// yields flat prior on abs(cor)<.7, and diminishing to zero by abs(cor)==1
// view in R via: hist(tanh(abs(rnorm(1e7)*.74)),br=1e4,xlim=c(0,1))
corz_vec ~ normal(0,.74) ;
////
// Likelihood
////
// looping over coefs to express structure that each is normally distributed
// (could this part be replaced with separate expressions for the sampling distribution of the mean and SD?)
for(this_coef in 1:num_coef){
subj_coef_mat[,this_coef] ~ normal(mean_coef[this_coef],sd_coef[this_coef]);
}
// expressing the structure for the pairwise correlations
obs_z ~ normal( corz_vec , corz_se ) ;
}
generated quantities{
// cor_vec: the upper-tri of the correlation matrix, flattened to a vector for efficient storage
vector[num_cors] cor_vec = tanh(corz_vec) ;
}
And with this model we get the calibration we expect on even the high correlations:
(omitted for brevity: plots of the no-high-correlations scenario and binomial tests of calibration, all showing good performance of this second model)