Has anyone seen examples of expert knowledge elicitation of probabilities using Bayesian inference?
Section 6.3 in this paper describes the general idea I am on the lookout for, but is a bit light on examples and prior work.
To be more concrete, let us assume we have a coin with an unknown bias and an appropriate prior (e.g. symmetric beta or uniform). Now let’s assume we ask multiple experts about the coin. Different questions could be:
- what side is going to come up?
- what do you think the probability of heads is?
- using N chips, how would you distribute them between heads and tails in a roulette scenario to maximize your expected winnings?
What would be a reasonable observation model for the expert responses? For the first type of response, should we consider it on equal par with an observation of the coin or should we use some second-order notion, i.e. the expert’s hypothetical coin is generated from the same hierarchical prior as the true coin enabling a sort of pooling? Should we take into account that the expert is solving a decision problem?
I think the last type of response is most interesting since there’s both a high amount of information in the response and it articulates probabilities in a relatable manner, but the observation model seems challenging. Maybe one could consider the chips as drawn from a multinomial distribution and pool with the true random process using a beta/dirichlet prior?
Another option would be to consider his response as being based on a latent dataset of draws experienced by the expert, with his response being either a draw from or a maximum over his personal posterior belief.
Have you seen SHELF ? More specifically, maybe Savchuk & Matz, 1994 is worth looking into.
I think I stumbled across MATCH, but it seems that both are just fitting densities directly to the expert judgment? The third response in my list corresponds to their roulette method, but I have seen it called bins and chips elsewhere.
This is probably not an immensely problematic way to go about it as we are just using it to construct a reasonable prior, but I still think it would be interesting to see the same kind of elicitation in a fully Bayesian setting. Your second article looks interesting, I’ll take a look, thanks!
I don’t have a reference or any experience doing this, but I have always believed the quantile function is the easiest thing to elicit with. I talked about this a little bit on pages 8 – 10 of https://mc-stan.org/workshops/Rmedicine2018/ . Basically, there are these quantile parameterized distributions — which are distributions whose parameters are quantiles — that I implemented in “Helper functions”. So, you can asked the purported expert things like “What would be your over / under (median) on this unknown?” or “If I gave you three-to-one odds, at what point would you switch which side you bet on?”. Basically, you can elicit quantiles without necessarily using the word quantile and then directly plug in the answers as parameters in the appropriate (for the parameter space) quantile function.
1 Like
Hadn’t heard about the quantile parameterized distributions before, that’s a pretty nifty trick. Although the construction seems a bit obtuse; it’s flexible for sure, but within the family of distributions with particular 25-50-75 quantiles it’s unclear what the QPD selects for aside from smoothness? I assume there is no obvious maximum-entropy argument given that they are unlikely to be in the exponential family…
That aside, while QPD is a good elicitation strategy, it’s not really Bayesian in the sense I was looking for. It seems that QPD is fit with least-squares (or simple matrix inverse), but what if we wanted to add the expert to our full joint model as an observation and then condition on him?
AFAIK, there are only a few quantile parameterized distributions:
- metalogistic when the parameter space is all real numbers
- q-normal when the parameter space is all real numbers
- transformations based on the normal or logistic distribution when the parameter space is bounded on one or both sides
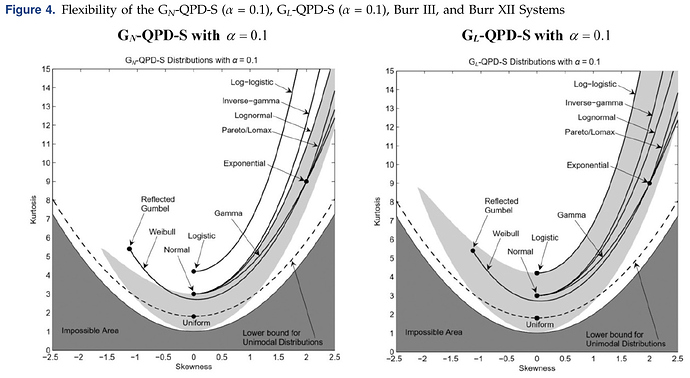
So, there are not really enough choices to get overly concerned about choosing within the applicable family. But the papers on http://www.metalogdistributions.com/publications.html do have some justifications in them. The metalogistic is essentially a Taylor series and so it could approximate anything analytic with enough terms. There is a more recent paper that shows transformations of the logistic do a better job than the normal at covering possible combinations of skewness and kurtosis (in light grey)
For the metalogistic and the q-normal, the first step is to elicit pairs of p and \theta from the expert and then in the second step, the prior is formed by doing a least-squares thing on what the expert said. Then in the subsequent steps, you condition on the data to get posterior pairs of p and \theta. So, it is fully compatible with Bayesian inference, although you would need to model the dependence between the unknowns in your model.
3 Likes