Hi everyone,
I made an attempt to code up the Double Pareto LogNormal Distribution in Stan. The attached R file shows DPLN data generation using equation 6 of Reed and Jorgensen (https://www.math.uvic.ca/faculty/reed/dPlN.3.pdf) and the file DPLN-fit.stan fits the model using the pdf in the form of equations 8 and 9 (noting the typo in Eq 9, where alpha should be theta). I wrote two different version of the function, one which takes in scalars and one for vectors (I comment out the one I don’t want as I go), but the guts are the same.
The model with the vector version of the function is:
functions {
real dpln_log(vector x, real alpha, real beta, real nu, real tau){
vector[num_elements(x)] prob;
real lprob;
real leadfraction;
leadfraction <- (alpha*beta)/(alpha + beta);
for(i in 1:num_elements(x)){
prob[i] <- leadfraction*( exp(alpha*nu + 0.5*square(alpha*tau))*pow(x[i],(-alpha-1))*Phi(inv(tau)*(log(x[i]) - nu - alpha*square(tau))) + exp(-beta*nu + 0.5*square(beta*tau))*pow(x[i],(beta-1))*(1 - Phi(inv(tau)*(log(x[i]) - nu + beta*square(tau)))) );
}
lprob <- sum(log(prob));
return lprob;
}
}
data {
int N;
vector[N] x;
}
parameters {
real<lower=0> alpha;
real<lower=0> beta;
real nu;
real<lower=0> tau;
}
model {
// priors
alpha ~ cauchy(0,5);
beta ~ cauchy(0,5);
nu ~ normal(0,50);
tau ~ cauchy(0,5);
// likelihood
x ~ dpln(alpha, beta, nu, tau);
}
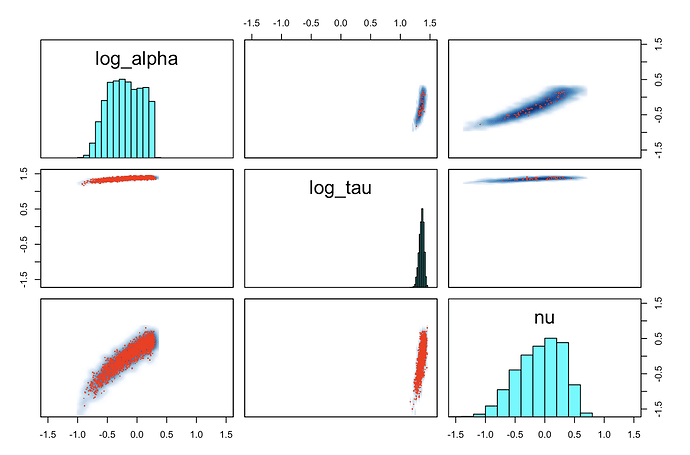
The sampling behaviour is very unhealthy and the inference is mediocre (although actually sometimes ok, and usually in fact not as bad as it should be given how bad the sampling is!). The attached traceplots show something weird: some of the chains look ok but some are essentially degenerate / perfectly autocorrelated. I haven’t see this happen before. Is anyone familiar with these patterns, or alternatively, with these kinds of composite distributions?
As you can see, the number of effective draws is laughable in this case, but I noticed it’s also quite variable across runs:
I may have made a typo in the definition of the function – but the presence of the good chains makes me think it’s not that. Also, I did check that my function can be used to generate data that looks approximately right to me when I switch the parameters / data blocks around (see second part of the attached R file and the DPLN-generate.stan files – yes I did it in the model block, I see this as a check not a serious data generation attempt, and I include it just in the interest of completeness).
The DPLN might just be a badly-behaved distribution, and certainly it only has moments smaller than the alpha parameter, but I have tried with larger values of alpha (eg 10) and did not see much improvement.
I wondered if the half-cauchy priors are just too wide for this relatively complex distribution, and I tried once with tighter!half-normal priors – that actually made it worse, all the chains were badly autocorrelated. Curious!
Any insight much appreciated! Hopefully once we get to the bottom of this all stan users will be able to enjoy the DPLN. :)
Cheers
Rachael
DPLN-fit.stan (1.3 KB)
DPLN-generate.stan (1.2 KB)
DPLN-test.R (2.2 KB)