Diagnosing convergence under label-switching

[g_lewis]

Hi all,
This is a little different than other label-switching questions I’ve found here, and it’s not really covered by Betancourt’s excellent vignette. Sorry for the long post. The quick summary is that I’m facing label-switching, which isn’t a problem for my application except that it messes up diagnostics such as R-hat and ESS. Correcting for label-switching (post-hoc relabeling) makes the diagnostics much better, but I still seem to need long-ish runs (8 chains, 4000 warmup, 5000 sampling so far) to make the corrected diagnostics closer to the recommended values (still not there yet), perhaps indicating deeper issues with sampling.

More detail:

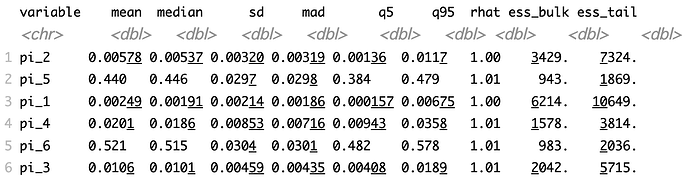
I am using a fully exchangeable mixture of 6 multivariate Gaussians as a prior on hierarchical regression coefficients (vectors length 3). I don’t mind label-switching itself in my MCMC chains, since I’m not trying to make (unidentifiable) inferences about specific mixture components. And if I use careful priors, cmdstanr’s HMC sampling runs fairly quickly without divergences, so I don’t think it’s crazy to fit 6 multivariate components. But the R-hat and ESS automatically produced by cmdstanr look terrible (see below; these are the estimated mixture weights \pi).

Now, we know that label-switching, or more precisely exchangeability, can fool naive R-hat: e.g. R-hat doesn’t know that a chain sampling near mode (\theta_1 = 0, \theta_2 = 1) is actually equivalent to that chain sampling near mode (\theta_1 = 1, \theta_2 = 0) if these parameters are exchangeable. So it can look like two chains haven’t mixed, or one chain isn’t stationary (e.g. first half of the chain appears to be sampling a different mode than the second half) — when actually all is well. That is what I’m hoping is causing most of the problem.

So currently I’ve been doing the very simplest post-hoc relabeling (there’s a whole literature on this that I’ve been trying desperately to ignore). After sampling, within each chain, for each iteration/draw, I (arbitrarily) re-order the mixture indices by the size of the mixture weight (i.e. I re-order so that mixture weights \pi_1 < \pi_2 < \dots). Exchangeability says this is valid. And R-hat and ESS do look dramatically better for the variables that have had their indices re-ordered.

After:

But R-hat and ESS vary a lot between mixture components, and there’s a slightly fishy pattern that after re-ordering the larger mixture weights tend to have much worse diagnostics, not sure if that’s indicative of something.

So I’m looking for an explanation and a better solution. One obvious possibility is to change the model so that the mixture weights are an ordered simplex. But there seems to be confusion in the Stan forums about whether that’s slow or unstable or plain dumb, and I don’t have a good intuition about sensible ordered simplex priors (or what it would mean to declare an ordered Dirichlet). And the other symmetry-breaking schemes don’t play nicely with my multivariate model (and frankly look like pretty weird priors).

[avehtari]

If there is overlap in the mixture weight distributions, re-ordering can cause dependency, too. In your “After” table, the diagnostic looks just fine.

[g_lewis]

Thanks, Dr. Vehtari! That makes sense about creating correlations —I’m imagining starting with an uncorrelated 2d distribution that spans the 45 degree line (overlap); folding the distribution along the 45 degree line then creates a correlated distribution. Perhaps you’re saying that this can produce low ESS/high R-hat without an actual problem in sampling?

I’m still trying to gain an intuition for whether there’s a real problem in my case, where ESS for my biggest mode looks like it’s just under the recommended 1,000 — partly because my real ambition is to use many more than 6 components so it’s a closer approximation of a Dirichlet Process mixture model, and I expect this seemingly-low-ESS phenomenon to get worse with more components.

[Bob_Carpenter]

@g_lewis

Now, we know that label-switching, or more precisely exchangeability, can fool naive R-hat:

There are multiple ways of looking at this. R-hat’s just measuring that each chain gets the same answer. When there’s label switching, each chain does not get the same answer if you use the labels. On the other hand, if you marginalize the labels out in the expectations you evaluate, then the problem goes away.

@g_lewis

just under the recommended 1,000

That should be more than enough for inference. We usually recommend on the order of 100. The standard error will be the posterior standard deviation divided by the square root of the effective sample size.

@g_lewis

Exchangeability says this is valid.

I’m afraid this isn’t legal. Here’s a simple example to illustrate. I’ll use the simplest possible exchangeable distribution, a 2D standard normal.

y ~ \text{normal}(0, \text{I}_2),

If we order each row so that the largest element is in the first column and the smallest in the second column, you’re going to distort the posterior means. Here’s an example.

> X <- matrix(rnorm(2000), nrow = 1000, ncol = 2)

> X <- cbind(pmin(X[, 1], X[, 2]), pmax(X[, 1], X[, 2]))

> colMeans(X)
[1] -0.5691052  0.5481322

> sd(X[, 1])
[1] 0.8475725

> sd(X[, 2])
[1] 0.8356001

These are the means and standard deviations of the order statistics of two standard normals.

You can, on the other hand, order the parameters in the model, as that’s going to preserve uncertainties properly. @betanalpha has a nice case study here:

Identifying Bayesian Mixture Models

@g_lewis

One obvious possibility is to change the model so that the mixture weights are an ordered simplex. But there seems to be confusion in the Stan forums about whether that’s slow or unstable or plain dumb

I’m not sure what you’re seeing here, but if it’s a mixture, then the mixture weights will be a simplex. I’m not sure what you mean by “ordered simplex”—you mean making sure the component balances are the same? You can do that in the prior. Declaring an “ordered Dirichlet” is easy, but it doesn’t lead to ordered simplexes. To create an ordered simplex you can do this:

parameters {
  pos_ordered[N] x;
}
transformed parameters {
  simplex[N] theta = softmax(x);
}

Without any other constraints, this is going to give you an improper posterior because pos_ordered is unbounded (above—it’s bounded below). But if you have other constraints on theta it might be OK.

It’s more typical to order the means of the mixture components than to order the simplex.

[g_lewis]

@Bob_Carpenter

if you marginalize the labels out in the expectations you evaluate, then the problem goes away.

I agree that label-switching is not a problem for posterior inferences from a model that ran properly; but as I said in the original post, I’m trying to diagnose convergence.

@Bob_Carpenter

That should be more than enough for inference.

Great to hear! Hoping this holds up in bigger models — the pattern of declining ESS in the larger mixture components isn’t encouraging.

@Bob_Carpenter

I’m afraid this isn’t legal.

At least for posterior inferences, I don’t think I’m breaking the law you’re warning about. Yes, sorting the elements of a random vector means that the first element of the sorted vector now has a different distribution than the first element of the original vector, as shown in your example. But because I know my model is exchangeable, for posterior inferences I’m only interested in exchangeable functions of the parameters (e.g. an order statistic of the random vector). So in your example, it’d be precisely the distribution of the row-wise max or min (or average, sum, etc) that I’d care about; sorting each row won’t give me the wrong distribution, provided I don’t misinterpret the result.

For diagnostics, it seems to follow that post-hoc relabeling the parameters according to the size of the mixture weights in each simulation should be fine — if it’s ok to check the MCMC convergence of the variables corresponding to the order statistics of the mixture weights. Is it not? Surely if these are sampling fine, then so are the parameters before relabeling? Maybe I’m missing something about how the diagnostics work.

@Bob_Carpenter

You can, on the other hand, order the parameters in the model, as that’s going to preserve uncertainties properly. @betanalpha has a nice case study

Yes, I’d really prefer to implement the solution where @betanalpha keeps the same exchangeable prior while enforcing an ordering during simulations (instead of post-hoc as I’ve done). But just for reasons of simplicity I’ve been reluctant to break apart my multivariate Gaussian mean-vectors only to arbitrarily order one of their elements (I understand it’s completely valid mathematically). Also, it’s more relevant and interpretable for me to directly get a posterior for the largest, smallest, etc. mixture weight.

So (little knowing how complicated my pursuit of simplicity would become!) that’s why I asked about an “ordered simplex” distribution. By that I meant the distribution of a random vector that obeys the simplex constraint and the further constraint that the elements of the random vector are ordered. One example (I know Stan wouldn’t implement it this way) is the distribution induced by drawing Dirichlet vectors and keeping only draws that satisfy the ordering, similar to the \pi' distribution in the case study — which would be great for me, but is apparently not the distribution created in Stan you try to declare an ordered simplex with a Dirichlet prior.

[True, the “ordered simplex” scheme I describe wouldn’t produce Dirichlets — but as @betanalpha shows, all exchangeable functions of the resulting vectors would behave exactly as though they contained Dirichlets, good enough for me].

Sorry for these giant messages, just trying to be clear. And despite my quibbling, everyone’s input is greatly appreciated.

[Bob_Carpenter]

@g_lewis

as I said in the original post, I’m trying to diagnose convergence.

You can diagnose convergence with the quantities of interest. Technically, you do not achieve convergence of label IDs when you have switching.

@g_lewis

the pattern of declining ESS in the larger mixture components isn’t encouraging.

Is this real or simulated data? If the model doesn’t match the data generating process, ESS typically suffers and if the misspecification is too bad, it can seriously hinder sampling.

@g_lewis

I don’t think I’m breaking the law you’re warning about.

:-). I don’t make the laws or even enforce them. The problems arise when the uncertainties overlap in the two cases. For example, if I have a mixture of normal(-1, 1) and normal(1, 1), then there’s going to be a lot of overlap in their uncertainties and I can’t disentangle a draw as coming from one or the other other than probabilistically (that is, I can figure out the posterior probability of the component responsible).

@g_lewis

“ordered simplex” distribution. By that I meant the distribution of a random vector that obeys the simplex constraint and the further constraint that the elements of the random vector are ordered.

@g_lewis

Maybe I’m missing something about how the diagnostics work.

The diagnostics like ESS and R-hat assume the input is a Markov chain, not something that you have permuted. For example, if you take the output draws from a Markov chain and then permute them, you’ll find that ESS improves dramatically even though your inferences don’t change at all (you still use the plug-in).

@g_lewis

little knowing how complicated my pursuit of simplicity would become

Mixtures are a pain! They tend to also be unstable computationally. They have problems with components dropping to size 1 and variance dropping to zero (which David MacKay describes as “EM goes boom” in his book when using EM to fit, but the same problems arise in Bayesian inference).

I’m still a bit unclear on what you mean by ordered Dirichlet. Just so we’re on the same page, there’s no parameterization alpha of theta ~ dirichlet(alpha) that will lead to theta’s components being ordered. If the gaps between the alpha are big enough, then you will expect outputs that are ordered, but it’s a very crude way to control it. You can do this:

theta ~ dirichlet(alpha);
theta_sorted = sort_asc(theta);

The random variable theta_sorted does not have a Dirichlet distribution. This is what I meant by sorting destroying the distributional properties. But then a dirichlet isn’t exchangeable unless alpha is constant. For example if I take a Dirichlet like this

theta ~ dirichlet(rep_vector(a, 10));

then the theta components are exchangeable. But even then, sort_asc(theta) does not have a Dirichlet distribution.

You can also use rejection sampling to keep drawing from a Dirichlet and throwing out anything that’s not ordered. The resulting random variable you are sampling does not have a Dirichlet distribution.