I want to compare two models with WAIC/PSIS, see the code below (the models were reparametrised for better sampling). First model describes a single normally distributed population, and the second model is mixture of two normal populations. In simple language, I want to see if there is one or two populations in my data, according to the models.
Question: what should I use in the “generated quantities” blocks for lpd_pointwise[i] = ... for each model? These are log probability density values for each data point used by WAIC and PSIS.
My brain is too stupid for this :).
Model 1: single gaussian
// Single Gaussian population model
data {
int<lower=1> n; // Number of data points
real y[n]; // Observed values
real uncertainties[n]; // Uncertainties
real sigma_stdev_prior;// Prior for standard deviation of population spread
}
parameters {
real mu; // Population location
real<lower=0> sigma; // Population spread
// Normally distributed variable
vector[n] z1;
}
transformed parameters {
// Non-centered parametrization
vector[n] y_mix1 = mu + sigma*z1;
}
model {
// Set priors
sigma ~ normal(0, sigma_stdev_prior);
mu ~ normal(0, 1);
// Normally distributed variables for non-centered parametrisation
z1 ~ std_normal();
// Loop through observed values and calculate their probabilities
// for a Gaussian distribution, accounting for uncertainty of each measurent
for (i in 1:n) {
target += normal_lpdf(y[i] | y_mix1[i], uncertainties[i]);
}
}
generated quantities{
vector[n] lpd_pointwise;
for (i in 1:n) {
lpd_pointwise[i] = ???
}
}
Model 1: mixture of two gaussians
// Guassian mixture model
data {
int<lower=1> n; // Number of data points
real y[n]; // Observed values
real uncertainties[n]; // Uncertainties
real sigma_stdev_prior;// Prior for standard deviation of population spread
}
parameters {
real<lower=0,upper=1> r; // Mixing proportion
ordered[2] mu; // Locations of mixture components
real<lower=0> sigma; // Spread of mixture components
// Normally distributed variables
vector[n] z1;
vector[n] z2;
}
transformed parameters {
// Non-centered parametrization
vector[n] y_mix1 = mu[1] + sigma*z1;
vector[n] y_mix2 = mu[2] + sigma*z2;
}
model {
// Set priors
sigma ~ normal(0, sigma_stdev_prior);
mu[1] ~ normal(0, 1);
mu[2] ~ normal(0, 1);
r ~ beta(2, 2);
// Normally distributed variables for non-centered parametrisation
z1 ~ std_normal();
z2 ~ std_normal();
// Loop through observed values
// and mix two Gaussian components accounting for uncertainty
// of each measurent
for (i in 1:n) {
target += log_mix(1 - r,
normal_lpdf(y[i] | y_mix1[i], uncertainties[i]),
normal_lpdf(y[i] | y_mix2[i], uncertainties[i]));
}
}
generated quantities{
vector[n] lpd_pointwise;
for (i in 1:n) {
lpd_pointwise[i] = ???
}
}
What I tried (and failed)
I naively tried copy-pasting code from model block into generated quantities. For single gaussian model:
lpd_pointwise[i] = normal_lpdf(y[i] | y_mix1[i], uncertainties[i]);
and this for the two gaussians:
lpd_pointwise[i] = log_mix(1 - r,
normal_lpdf(y[i] | y_mix1[i], uncertainties[i]),
normal_lpdf(y[i] | y_mix2[i], uncertainties[i]));
This did not work because in the two-gaussian model the results from normal_lpdf functions are multiplied by (1 - r) and r. And if, for example, r is 0.5 (equal mixture of two gaussians), and a data point is above the peak of the first gaussian, the result of the log_mix function will be about two times smaller than the result from normal_lpdf in the single gaussian model (I plotted posterior distribution on Fig. 4, 5 to help visualise this). Since WAIC are just sums of the log of mean probability density values across sampling iterations (minus effective number of parameters), and the log probability densities for the two-gaussian model are about two times smaller, it follows that the WAIC for the two-gaussian model would also be about two times lower than than that from the single-gaussian model. As a result, the model comparison will always prefer a single-gaussian model, even if the data come clearly from two populations. We are comparing apples with oranges here, I think.
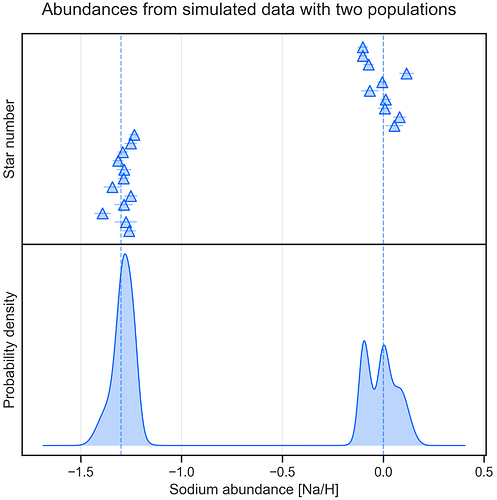
I checked this by synthesising observations with two very distinct gaussian populations shown on Fig.1. Both WAIC and PSIS preferred single gaussian model (see Fig. 2 and 3).
Figure 1: Synthesised observations
Figure 2: Comparing models with WAIC
Figure 3: Comparing models with PSIS
Plots of observations and posterior distributions
The thick line on bottom halves of the plots is probability density of observations (not posterior mean). The multiple thin lines are posterior distributions from first 50 iterations. The dashed vertical lines are “true” locations of two synthesised populations.
Figure 4: posterior distributions from one-gaussian model
Figure 5: posterior distributions from two-gaussian model
Full code
The full code to compare the models and make the above plots is located here: