time_cost_calculated.CSV (1.9 MB)
mtc_equity-v4.R (2.2 KB)
I’ve been working on this model for a few months to get it running in a reasonable time. I now have it running but am having some divergence issues. I’m running it again with a higher adapt_delta (0.9 vs. 0.8) and additional warmup iterations, but I know that’s not the preferred solution. The model is being run on a GPU with 9 threads per chain, so I wondered if having so many independent threads might be affecting the results. I currently use the default init values.
I was also thinking it might be helpful to check my prior predictive distribution, but I haven’t done that before. This is a simplified model from a version that will have additional contextual variables in a[n] that describe person attributes. The hope is to also introduce correlation between some parameters.
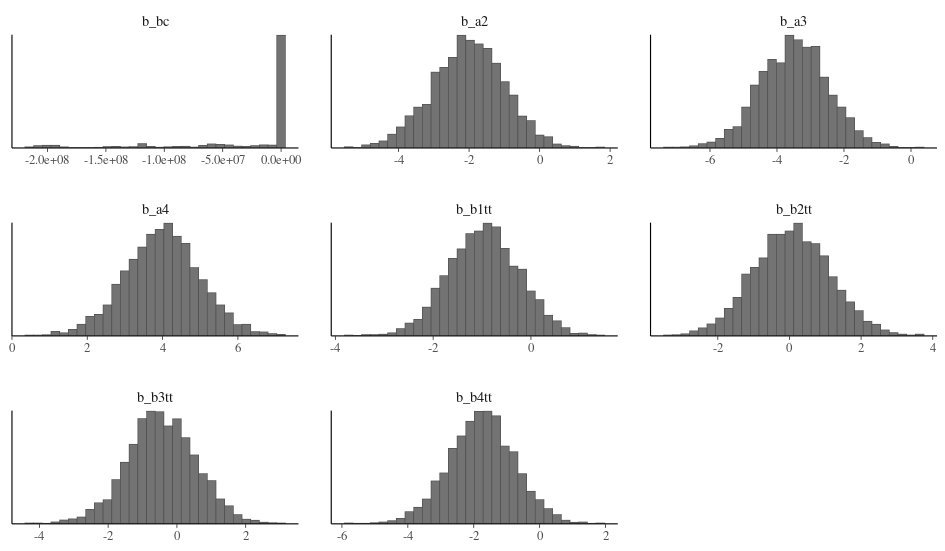
I’d adjusted my priors based on a previous run, but they are clearly not exploring the full parameter space. I tried some visual diagnostics.
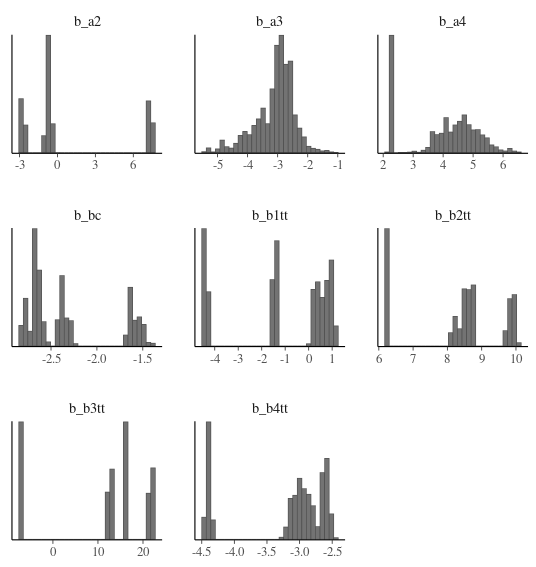
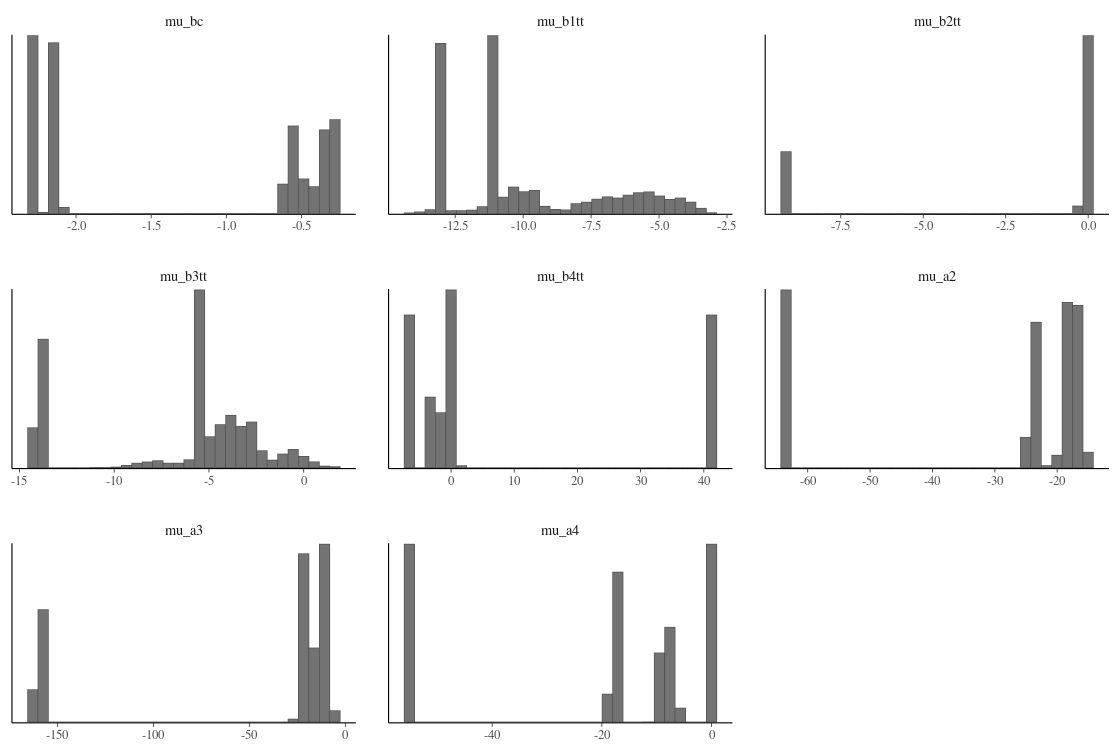
My parameter plot looks quite different from the examples. There seem to be a few tight regions explored across iterations.
My standard deviations are also clustered rather than having the normal distribution found in the online examples. Either they are truly multi-modal or my model/priors are wrong.
Same pattern for the beta parameters.
functions {
int[] sequence(int start, int end) {
int seq[end - start + 1];
for (n in 1:num_elements(seq)) {
seq[n] = n + start - 1;
}
return seq;
}
real partial_log_lik_lpmf(int[] seq, int start, int end,
data int ncat, data int nvar, data int ntotvar, data int[] Y, data matrix x1, data matrix x2, data matrix x3, data matrix x4, data int[] J_1, data int[] J_2, matrix r_1, matrix r_2,
real b_a2, real b_a3, real b_a4, real b_btc, real b_b1tt, real b_b2tt, real b_b3tt, real b_b4tt) {
real ptarget = 0;
int N = end - start + 1;
// Define matrices/vector for x, alpha, beta
matrix[ncat,nvar] x;
vector[ncat] alpha;
matrix[nvar,ncat] beta;
array[N] row_vector[ncat] a = rep_array([0,b_a2,b_a3,b_a4], N);
// initialize linear predictor term
// Terms are btc, b1tt, b2tt, b3tt, b4tt
array[N] row_vector[ntotvar] b = rep_array([b_btc,b_b1tt,b_b2tt,b_b3tt,b_b4tt], N);
for (n in 1:N) {
int nn = n + start - 1;
// add to linear predictor term
a[n] += [0,r_1[J_1[nn],1] + r_2[J_2[nn],1], r_1[J_1[nn],2] + r_2[J_2[nn],2], r_1[J_1[nn],3] + r_2[J_2[nn],3]];
// add to linear predictor term
// Terms are btc, b1tt, b2tt, b3tt, b4tt
b[n] += [r_1[J_1[nn],4] + r_2[J_2[nn],4], r_1[J_1[nn],5] + r_2[J_2[nn],5], r_1[J_1[nn],6] + r_2[J_2[nn],6],r_1[J_1[nn],7] + r_2[J_2[nn],7],r_1[J_1[nn],8] + r_2[J_2[nn],8]];
b[n] = exp(b[n]);
// Each x and beta is a matrix with dimensions alts x variables
// Our x will be the time/cost coming in as inputs
x = to_matrix([x1[nn],x2[nn],x3[nn],x4[nn]]);
// Our betas will be the hierarchical slope parameters (2 x 4)
beta = [b[n,1] * b[n,2:5], rep_row_vector(b[n,1],ncat)];
// Our alphas will be the hierarchical intercept parameters
alpha = [a[n,1], b[n,1] * a[n,2], b[n,1] * a[n,3], b[n,1] * a[n,4]]';
ptarget += categorical_logit_glm_lupmf(Y[nn] | x, alpha, beta);
}
return ptarget;
}
}
data {
int<lower=1> N; // total number of observations
int<lower=2> ncat; // number of categories
int<lower=2> nvar; // number of variables for each alternative
int<lower=2> ntotvar; // number of total variables
int grainsize; // grainsize for threading
array[N] int Y; // response variable
// covariate matrix for alt1
matrix[N,nvar] x1; // matrix[N,nvar] x1;
// covariate matrix for alt2
matrix[N,nvar] x2; // matrix[N,nvar] x2;
// covariate matrix for alt3
matrix[N,nvar] x3; // matrix[N,nvar] x3;
// covariate matrix for alt4
matrix[N,nvar] x4; // matrix[N,nvar] x4;
// data for group-level effects of ID 1
int<lower=1> N_1; // number of grouping levels
int<lower=1> M_1; // number of coefficients per level
array[N] int<lower=1> J_1; // grouping indicator per observation
// group-level predictor values
int<lower=1> NC_1; // number of group-level correlations
// data for group-level effects of ID 2
int<lower=1> N_2; // number of grouping levels
int<lower=1> M_2; // number of coefficients per level
array[N] int<lower=1> J_2; // grouping indicator per observation
int prior_only; // should the likelihood be ignored?
}
transformed data {
int seq[N] = sequence(1, N);
}
parameters {
real b_btc; // population-level effects
real b_a2; // population-level effects
real b_a3; // population-level effects
real b_a4; // population-level effects
real b_b1tt; // population-level effects
real b_b2tt; // population-level effects
real b_b3tt; // population-level effects
real b_b4tt; // population-level effects
row_vector<lower=0>[8] sd1; // group-level standard deviations
row_vector<lower=0>[8] sd2; // group-level standard deviations
matrix<multiplier = rep_matrix(sd1, N_1)>[N_1, 8] r_1;
matrix<multiplier = rep_matrix(sd2, N_2)>[N_2, 8] r_2;
}
model {
// likelihood including constants
if (!prior_only) {
target += reduce_sum(partial_log_lik_lpmf, seq,
grainsize, ncat, nvar, ntotvar, Y, x1, x2, x3, x4, J_1, J_2,
r_1, r_2, b_a2, b_a3, b_a4, b_btc, b_b1tt, b_b2tt, b_b3tt, b_b4tt);
}
// priors
target += normal_lpdf(b_btc | 0, 5);
target += normal_lpdf(b_a2 | 0, 25);
target += normal_lpdf(b_a3 | 0, 25);
target += normal_lpdf(b_a4 | 0, 25);
target += normal_lpdf(b_b1tt | 0, 5);
target += normal_lpdf(b_b2tt | 0, 2.5);
target += normal_lpdf(b_b3tt | 0, 1.5);
target += normal_lpdf(b_b4tt | 0, 5);
target += student_t_lpdf(sd1 | 3, 0, 2.5);
target += student_t_lpdf(sd2 | 3, 0, 2.5);
for (k in 1:8) {
r_1[, k] ~ normal(0, sd1[k]);
r_2[, k] ~ normal(0, sd2[k]);
}
}
}