Firstly we have to keep in mind that samples and contour slices do not visualize the same object. Contour slices visualize a conditional distribution, say one specified by the conditional density function
\pi(\theta_{1}, \theta_{2} \mid \theta_{3} = \tilde{\theta}_{3}, \ldots, \theta_{I} = \tilde{\theta}_{I})
where as projected samples visualize a marginal distribution, say one specified by the marginal density function
\pi(\theta_{1}, \theta_{2}) =
\int \mathrm{d} \theta_{3} \ldots \mathrm{d} \theta_{I} \,
\pi(\theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{I} ).
These will be different unless
\pi(\theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{I} )
=
\pi(\theta_{1}, \theta_{2}) \, \pi(\theta_{3}, \ldots, \theta_{I} )
in which case there’s no reason to consider \theta_{3}, \ldots, \theta_{I} at all.
Constructing contours for the marginal density would require be able to evaluate the marginal density function and hence the above integral, which is rarely feasible. At the same time conditional samples can be generated only be filtering the available samples around some tolerance of the conditioning values \tilde{\theta}_{3}, \ldots, \tilde{\theta}_{I}. For more than a few dimensions there is not much probability of having any samples within a small tolerance and increasing the tolerance to allow more samples distorts the local conditional behavior.*
Also I’ll mention my distaste for highest density posterior intervals which are parameterization dependance, not always well-defined especially in more than one-dimension, and prone to erratic behavior at higher probability containments.
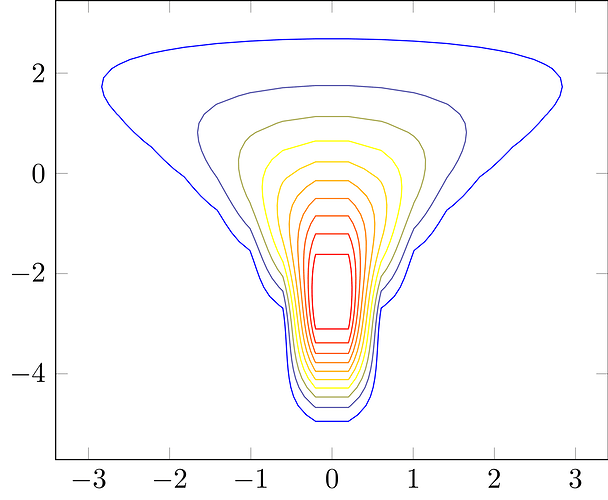
I’m not sure that there’s a solution adequate for the intended goal, but if we remove the samples and just consider the conditional contours then I’ve found that the trick is to use nonlinear levels; see for example Markov Chain Monte Carlo in Practice. This allows for a high density of level sets in regions of strong curvature and a lower density of level sets in regions of weaker curvature, although identifying a useful nonlinearity and then the right grid along the nonlinearity will in general be nontrivial.
*In theory this would be possible if one had access to the full numerical Hamiltonian trajectories and one ran those trajectories much, much longer than needed for statistical exploration. The resulting figure would resemble a Poincare section/map, Poincaré map - Wikipedia. Anyways very much not practical when working with Hamiltonian Monte Carlo output alone, but I wanted to mention it because the pictures are fun.