Hi Stan Forum!
I am currently trying to implement the use of the excellent projpred package (thanks @fweber144 and colleagues!) for variable selection with brms parametric survival models that use a Weibull response distribution (with the default scale = “log” and shape = “identity” link functions). As in Catalina (2021) you can use the latent space projection approach to do this. This works OK with the GitHub branch (v2.0.5.9000) that the authors refer to in the paper; however, I’m hoping to implement it in projpred v2.8.0 to make use of the latest features and as an exercise to improve my understanding.
Following the threads of the above paper – and other related posts on this forum and GitHub – to the relevant vignette and documentation, implementing Weibull models with projpred v.2.8.0 requires passing custom functions for latent_ilink(), latent_ll_oscale(), and latent_ppd_oscale() to extend_family(). Following the vignette, I’ve implemented these functions for the Weibull distribution as in the reprex below. This works and provides more-or-less identical results to projpred v2.0.5.9000 with the same (correct) variables being selected in the same order. Despite this, I have a few questions:
-
Have I implemented these
extend_family()functions correctly? -
projpred v2.0.5.9000sets the latent Weibull reference model dispersion parameter (dis) to1by default.projpred v2.8.0sets this toNA(presumably because there’s no default forweibullmodels); however, if I manually set this to1, I can fully reproduce the results fromprojpred v2.0.5.9000. My ignorance is on full display here, but given its presence inv2.0.5.9000, I assume this is an acceptable thing to do? -
Having to pass
refm_shapethrough tolatent_ll_oscale_weib()andlatent_ppd_oscale_weib()means that the parallelisation fails, as this global environment object isn’t exported to the parallel workers. I see this issue has been raised on GitHub, but I wondered if there’s a short-term workaround by manually editing the call toforeachdirectly? -
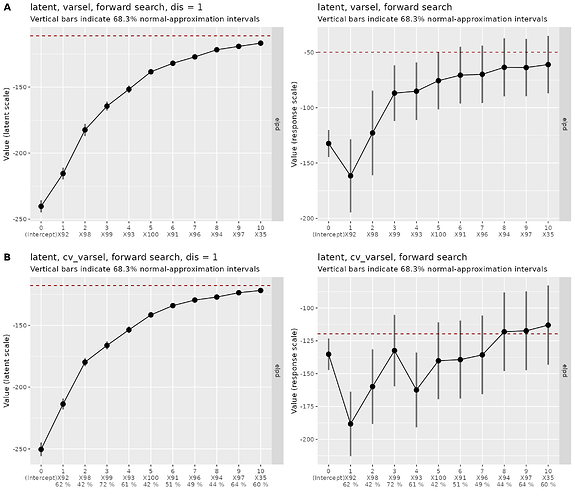
The
elpdplots look good when on the latent scale, but bad on the original response scale (resp_oscale = TRUE) – is this problematic? I assume this is kind of the point of the approach?
The actual problem case is very high-dimensional (p ~ 2,500, n ~ 250) and hierarchical in nature, but I’ve first simulated some simpler, non-hierarchical, lower-dimensional data (p = 100, n = 100) to make a reprex below.
## Packages ----
library(brms)
library(devtools)
library(dplyr)
library(MASS)
library(Matrix)
devtools::install_github("stan-dev/projpred", ref = "latent_projection") # v2.0.5.9000
library(projpred)
library(trialr)
## Simulate data ----
# Sample from LKJ distribution for a randomised correlation matrix
set.seed(1234)
cor_mat <- trialr::rlkjcorr(n = 1, K = 100, eta = 1)
# First and second variable sets correlate with each another within each set
cor_mat[91:95, 91:95] <- matrix(rep(0.5, times = 25), ncol = 5)
cor_mat[96:100, 96:100] <- matrix(rep(0.5, times = 25), ncol = 5)
# First and second variable sets do not correlate with one another between sets
cor_mat[91:95, 96:100] <- matrix(rep(0, times = 25))
cor_mat[96:100, 91:95] <- matrix(rep(0, times = 25))
diag(cor_mat) <- 1
# Sample some standard deviations of the variables
sd <- rgamma(100, 1, 2)
# Convert the correlation matrix to a covariance matrix
cov_mat <- diag(sd) %*% cor_mat %*% diag(sd)
# Sample variables from the multivariate normal distribution
vars <- MASS::mvrnorm(
n = 100
,mu = rnorm(100, 30, 2.5)
,Sigma = Matrix::nearPD(cov_mat)$mat
)
# Scale the variables
scaled_vars <- apply(vars, 2, scale, scale = TRUE)
# Draws from Weibull distribution where only the last set of variables have predictive information
shape <- 1.2
predictors <- scaled_vars[,91:100] %*% rep(c(0.5, -0.5), each = 5)
linpred <- exp(0 + predictors)
scale_pred <- linpred / (gamma(1 + (1 / shape))) # brms AFT parameterisation
y <- rweibull(
n = 100
,shape = shape
,scale = scale_pred
)
cens <- runif(100, 0, 4)
time <- pmin(y, cens)
status <- as.numeric(y <= cens)
df_sim <- data.frame(
time = time
,status = status
,censored = 1 - status
,vars
)
## Fit model with all variables (ignore a few divergent transitions for now)
model_hs <- brm(
time | cens(censored) ~ 1 + .
,family = weibull
,data = df_sim |> dplyr::select(-status)
,chains = 4
,iter = 3000
,prior = c(
prior(normal(0, 100), class = Intercept)
,prior(horseshoe(par_ratio = 0.1), class = b)
,prior(gamma(1, 0.5), class = shape)
)
,seed = 1234
,cores = 4
,control = list(adapt_delta = 0.95, max_treedepth = 15)
,save_pars = save_pars(all = TRUE)
)
## projpred v2.0.5.9000 ----
# Generate the reference model object with latent projection
refm_hs <- get_refmodel(model_hs, latent_proj = TRUE)
refm_hs$dis # all equal to 1 by default
ncores <- 10
doParallel::registerDoParallel(ncores)
# cv_varsel with official latent reference model
refm_hs_vsel_l1 <- cv_varsel(
refm_hs
,method = "L1" # purely for speed
,cv_method = "LOO" # purely for speed
,seed = 1234
,validate_search = TRUE
,parallel = TRUE
,nterms_max = 10
)
## projpred v2.8.0 ----
install.packages("projpred") # install v2.8.0 from CRAN
# Custom extend_family() functions for Weibull family latent projection as per
# https://mc-stan.org/projpred/articles/latent.html#negbinex
refm_shape <- as.matrix(model_hs)[, "shape", drop = FALSE]
latent_ilink_weib <- function(
lpreds
,cl_ref
,wdraws_ref = rep(1, length(cl_ref))
) {
ilpreds <- exp(lpreds) # mu parameter link = "log"
return(ilpreds)
}
latent_ll_oscale_weib <- function(
ilpreds
,y_oscale
,wobs = rep(1, length(y_oscale))
,cl_ref
,wdraws_ref = rep(1, length(cl_ref))
) {
y_oscale_mat <- matrix(
y_oscale
,nrow = nrow(ilpreds)
,ncol = ncol(ilpreds)
,byrow = TRUE
)
wobs_mat <- matrix(
wobs
,nrow = nrow(ilpreds)
,ncol = ncol(ilpreds)
,byrow = TRUE
)
refm_shape_agg <- cl_agg(refm_shape, cl = cl_ref, wdraws = wdraws_ref)
ll_unw <- dweibull(
y_oscale_mat
,shape = refm_shape_agg
,scale = ilpreds / gamma(1 + 1 / as.vector(refm_shape_agg)) # brms AFT parameterisation
,log = TRUE
)
return(wobs_mat * ll_unw)
}
latent_ppd_oscale_weib <- function(
ilpreds_resamp
,wobs
,cl_ref
,wdraws_ref = rep(1, length(cl_ref))
,idxs_prjdraws
) {
refm_shape_agg <- cl_agg(refm_shape, cl = cl_ref, wdraws = wdraws_ref)
refm_shape_agg_resamp <- refm_shape_agg[idxs_prjdraws, , drop = FALSE]
ppd <- rweibull(
prod(dim(ilpreds_resamp))
,shape = refm_shape_agg_resamp
,scale = ilpreds_resamp / gamma(1 + 1 / as.vector(refm_shape_agg_resamp)) # brms AFT
)
ppd <- matrix(ppd, nrow = nrow(ilpreds_resamp), ncol = ncol(ilpreds_resamp))
return(ppd)
}
# Generate the custom reference model object with latent projection
refm_hs_weib <- get_refmodel(
model_hs
,latent = TRUE
,dis = rep(1, times = 6000) # to match v2.0.5.9000
,latent_ilink = latent_ilink_weib
,latent_ll_oscale = latent_ll_oscale_weib
,latent_ppd_oscale = latent_ppd_oscale_weib
)
# cv_varsel with custom latent reference model
refm_hs_weib_vsel_l1 <- cv_varsel(
refm_hs_weib
,method = "L1" # purely for speed
,cv_method = "LOO" # purely for speed
,seed = 1234
,validate_search = TRUE
,parallel = FALSE # won't run due to `refm_shape`
,nterms_max = 10
)
# Check the selected predictors
identical(
refm_hs_vsel_l1$solution_terms
,refm_hs_weib_vsel_l1$predictor_ranking
) # TRUE
# Check the ELPD values (effectively identical)
round(refm_hs_vsel_l1$summary$elpd.loo, 1)
# [1] -239.5 -215.7 -186.3 -172.6 -165.6 -158.2 -151.5 -141.5 -134.5 -128.1 -126.7
round(summary(refm_hs_weib_vsel_l1, resp_oscale = FALSE)$perf_sub$elpd, 1)
# [1] -250.4 -226.3 -185.3 -177.7 -166.4 -159.2 -147.0 -135.5 -129.6 -126.7 -124.5
- Operating System: Ubuntu 24.04.2 LTS (running in WSL2)
- brms Version: 2.22.0
- projpred Version(s): 2.0.5.9000 and 2.8.0
- trialr Version: 0.1.6
Thanks in advance!