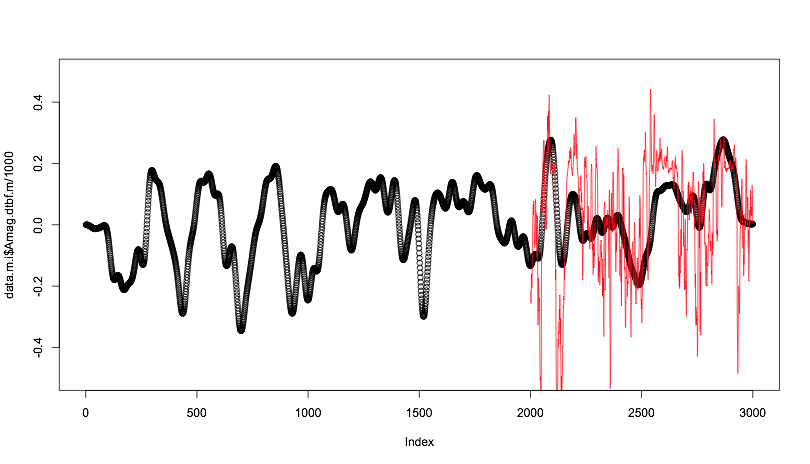
Real quick, I’ll respond to the other stuff in a bit, but
f = L * z + L being the Cholesky factor of a covariance of an RBF + z ~ normal(0, 1) implies that the prior on f is f ~ multi_normal(0, rbf_covariance)
So you don’t need g ~ normal(f, sigma_gp);
There are two hyperparameters of the RBF GP, one corresponding to the input scale (length scale, or rho in the manual) and one corresponding to the output scale (alpha in the manual). You can keep alpha outside the Cholesky – if that makes sense? Like, you can do the Cholesky assuming alpha = 1 and then scale the Cholesky as you like to still sample sigma. I’m probably not saying that clearly… Anyway, the thing you probably want is this:
transformed parameters {
vector[N] g = L * z * sigma_gp; // non-centered parameterization;
}
Along with z ~ normal(0, 1) to do the GP, and then get rid of g as an extra random variable.
Full modified model:
data {
int<lower=1> N; // number of (time) points in series
matrix[N,N] L;
int<lower=0> K; // number of predictos
matrix[N, K] X; // predictor design matrix
vector[N] response; // vector of Alongshore current speeds
//prediction
int<lower=1> S; // length of wind series to simulate over
int<lower=0> sK; // number of predictors for simulation
matrix[S, sK] SIM; // matrix of ismulated values
}
parameters {
vector[K] B; // coefficients of the model (both intercepts and slopes)
vector[N] z;
real<lower=0> sigma_response;
real<lower=0> sigma_gp;
real<lower=0> inv_rho_sq;
}
transformed parameters {
vector[N] g = L * z * sigma_gp; // non-centered parameterization;
}
model {
vector[N] mu;
B[1] ~ normal(0,1); // intercept prior
B[2:K] ~ normal(0,1); // slope priors
g ~ normal(0, 1);
z ~ normal(0, 1);
sigma_response ~ normal(0, 1);
sigma_gp ~ normal(0, 1);
mu = X * B + f ;
response ~ normal(mu, sigma_response);
}
generated quantities{
vector[S] sim_cur; //simulated response output
vector[N] mu_pred;
vector[N] pred_cur;
vector[N] log_lik;
vector[N] resids;
sim_cur = SIM * B; // simulated response across the range of params
mu_pred = X*B + g; //+ approx_L(M, scale, Distance, inv_rho_sq) * g;
for(i in 1:N){
pred_cur[i] = normal_rng(mu_pred[i], sigma_response); // posterior predictions of the model
log_lik[i] = normal_lpdf(response[i] | mu_pred[i], sigma_response); // compute log likelihood for us in AIC
}
resids = response - mu_pred;
}
Hahaha yeah, +1