Unexpected behavior when applying normal error to Inverse-Gamma distribution

[gregor]

Hi,

I’m an absolute newbie to the forums and fairly new to Stan + Bayesian Modeling, so please forgive the noobness of this question.

In a nutshell: I run into unexpected behavior when adding normally distributed error to an inverse-gamma distributed random variable. I’m almost certain this is because of misspecification (in line with the warnings I’m receiving) but I’d love some pointers as to why this is the case.

I’m simulating inverse-gamma distributed values (using PyStan) with

sim_code = """
data {
    int<lower=1> N;
}
generated quantities {
    real y[N];
    for (i in 1:N)
        y[i] = inv_gamma_rng(30, 300);
}
"""

sim = pystan.StanModel(model_code=sim_code).sampling(
    data={'N': 100},
    chains=1,
    iter=1,
    seed=17,
    warmup=0,
    algorithm='Fixed_param'
)

As expected I can recover alpha=30, beta=300 perfectly with

data {
    int<lower=1> N;
    real y[N];
}
parameters {
    real<lower=0> alpha;
    real<lower=0> beta;
}
model {
    y ~ inv_gamma(alpha, beta);
}

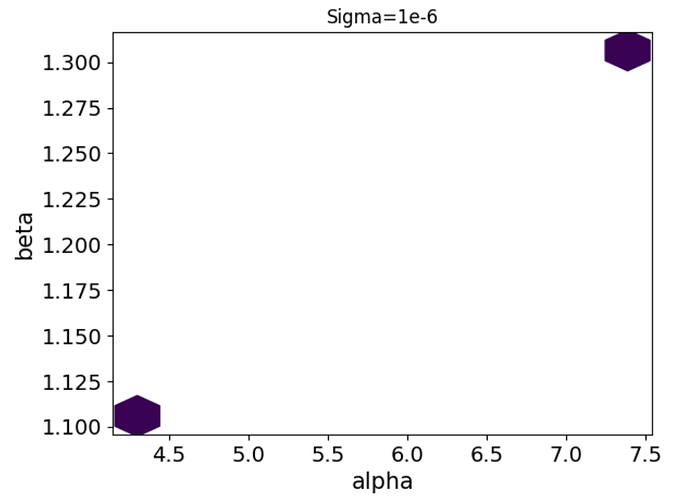
However, if I assume there’s additional normally distributed error, I receive E-BFMI warnings, a handful of divergences, and a weirdly bi-modal distribution of alphas and betas which is way off. Here’s the code I’m using:

data {
    int<lower=1> N;
    real y[N];
}
transformed data {
    real sigma = .001;
}
parameters {
    real<lower=0> alpha;
    real<lower=0> beta;
    real<lower=0> noise_free_y[N];
}

model {
    noise_free_y ~ inv_gamma(alpha, beta);
    y ~ normal(noise_free_y, sigma);
}

Of course, there is no normally distributed error in my simulation but my understanding would be that wrapping the inverse-gamma distribution with a normal distribution (here with marginal variance) should not corrupt the model. What am I missing?

Few notes:

• I deliberately left out priors here to keep things brief, in this simple example I would expect negligible impact
• In case you’re wondering why I’m considering adding normally distributed error: I’m planning to regress on y using additional variables linearly summed with the inverse-gamma random variables
• I’m aware of this but feels this goes deeper than needed at the moment

Thanks in advance for engaging on this basic matter!

[mike-lawrence]

Can you post the pairs plot for alpha & beta?

[gregor]

@mike-lawrence Thanks for getting back to me on this!

For the first model (without normal noise) the pairs plot look like expected:

For the second model with normal noise the pairs plot exhibit the weirdly bimodal behavior while being totally off:

I might be missing something obvious here, curious for pointers

BTW: I pulled the pairs plots using arviz. Not sure if there’s a better/nicer way for Python

[mike-lawrence]

I wonder if the scale of the true values being so far from the typical initialisation range is part of the problem. How does it perform when you do:

data {
    int<lower=1> N;
    real y[N];
}
transformed data {
    real sigma = .001;
}
parameters {
    real<lower=0> alpha;
    real<lower=0> beta;
    real<lower=0> noise_free_y[N];
}

model {
    alpha ~ std_normal();
    beta ~ std_normal();
    noise_free_y ~ inv_gamma(alpha*1e2, beta*1e3);
    y ~ normal(noise_free_y, sigma);
}

?

Also, try decreasing your input sigma to like 1e-6 then gradually increase to see if you can discern what is going on as it transitions from low-noise to higher-noise scenarios.

[gregor]

Hi @mike-lawrence, thanks a lot!

It seems your initial hunch was right but there’s another issue going on:

1. Setting inv_gamma(alpha*1e1, beta*1e2) does recover alpha and beta fairly closely (alpha*10=27, beta*100=280) [you suggested alpha*1e2, beta*1e3, I went with one order of magnitude lower matching those of the original values]

2. What’s still unclear to me is the effect of sigma: I was able to recover the values above using sigma=1. Setting sigma=1e-3 leads to 3/2000 divergences and a wrong bimodal parameter distribution, setting sigma=1e-6 leads to 1005/2000 divergences and an equally wrong bimodal parameter distribution. Higher noise, sigma=1, oddly seems to work fine. This is counterintuitive to me, unless the normal noise introduces some instabilities causing HMC to deteriorate (or there’s a simple mistake here somewhere).

For reference, here’s the code:

data {
    int<lower=1> N;
    real y[N];
}
transformed data {
    real sigma = 1;
}
parameters {
    real<lower=0> alpha;
    real<lower=0> beta;
    real<lower=0> noise_free_y[N];
}

model {
    alpha ~ std_normal();
    beta ~ std_normal();
    noise_free_y ~ inv_gamma(alpha*1e1, beta*1e2);
    y ~ normal(noise_free_y, sigma);
}
generated quantities {
    real noise_free_y_pred[N];
    real y_pred[N];
    for (i in 1:N) {
        noise_free_y_pred[i] = inv_gamma_rng(alpha*1e1, beta*1e2);
        y_pred[i] = normal_rng(inv_gamma_rng(alpha*1e1, beta*1e2), sigma);
    }
}