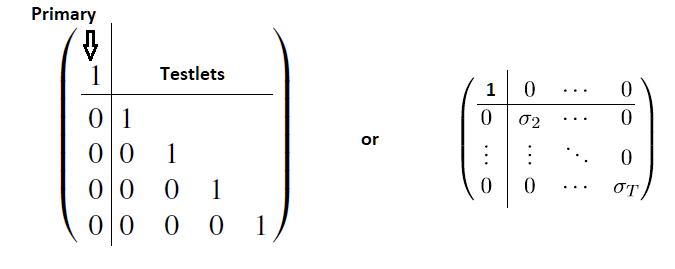Dear readers,
I want to implement an IRT testlet model and a kind oftwo-tier model (see Cai, 2010; https://link.springer.com/article/10.1007/s11336-010-9178-0) as an extention to that in brms. I wonder if this is possible in brms and how the corresponding formula might look. Let’s begin with a quick overview on my data structure.
I use a dataset of 74 items with 575 persons answering these items. The items are nested in testlets because they have to make multiple decissions (answer multiple items) to each of 17 item stems. The item stems can be assigned to different primary factors (one of three) in theory.
For a unidimensional 1PL model I came up with the following code:
formula_PCK_1D_1pl <- bf(
response ~ 1 + (1 | item) + (1 | ID) + (0 + testlet_char | ID),
family = brmsfamily("bernoulli", link = "logit")
)
The testlet assignment is given by an string. My problem is that I have to define a special covariance structure towards the model. In the unidimensional case it should have diagonal form. So there should be no correlation between the testlet factors and the testlet factors with the primary factor. Using the || operator semms not to set the correlation to 0 but just doesn’t calculate the cor, right?
I wondered if I could do something appropriate with the fcor term? Or setting lkj(100) to get at least very low correlations? How can I set up correlation between (1 | ID) and the (0 + testlet_char | ID) terms?
For a 3PL multidimensional model (where each item is assigned to exactly a single primary factor/dimension) I tried:
formula_PCK_3D_3pl <- bf(
response ~ gamma + (1 - gamma) * inv_logit(beta + exp(logalpha) * theta + testlet),
nl = TRUE,
theta ~ 0 + (0 + dimension_char | ID),
beta ~ 1 + (1 | item),
logalpha ~ 1 + (1 | item),
logitgamma ~ 1 + (1 | item),
nlf(gamma ~ inv_logit(logitgamma)),
testlet ~ 0 + (0 + testlet_char | ID)
family = brmsfamily("bernoulli", link = "identity")
)
Am I on the right way? Can you help me an formula for a dataset with, lets say, four different testlets?
Right now even the 1PL unidimensional models needs a huge amount of time to finish. I tried code for the rstan package as well which finishes much faster but doesn’t show convergance (for the code used see Luo et Jiao, 2018; https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6096466/). The modles via ML (mirt::bfactor, TAM::tam.fa) converged well for up to 2PL already.
- Operating System: Win 10x64 1909
- brms Version: 2.13.5
Sincerely, Simon