Truncated normal linear regression

Modeling
1

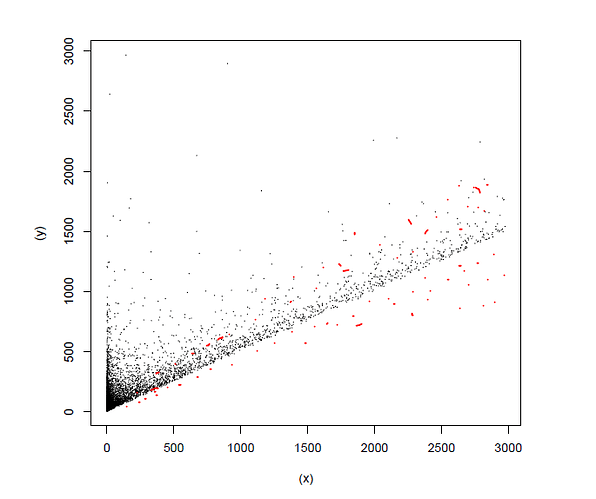
Hello,

I have a system where the noiseless data (BLACK dots) has a half normal-like regression

image.png685×574 25.6 KB

While the noise (RED dots) is heteroshedastic, and breaks the truncated data structure (or not?)

  1. Should I use a truncated linear regression?
  2. And what about the heterochedastic noise?
  3. In case, what is the best way to code truncate linear regression (y[n] ~ normal(x[n] * a, sigma) T[??,];)

Thanks

2

There’s a lot going on near small values, have you looked at the log-log plot for this data? It’s hard to say much without visualizing this more.

3

Yes,

even if the density is higher for small values it’s still linear.

At the moment I am using log log regression (especially for heterochedasticity), however for some low values there is some complication

Here is the log-log plot (noiseless)

image.png547×506 12.5 KB

4

I’m pretty sure you’ve posted this model before (or somebody else is working with the same data (?)). Doing a truncated model might work well if you have an expression for that line, it’s clearly not just half-normal on the lower end.

5

Quite some time ago, and it’s working well, in log-log version, but now before to close test I want to do the last check if better model is possible. (I approached truncated models just recently, and I had this thing in mind)

Do you mean log plot or raw plot? The log plot the line follows log(b0 + x * b1)

I would like truncated on raw data (NON-log transformed). What do you think?

6

I think the joy of discovery is well worth it.

7

Eheh, Yes at this stage the joy of discovery should be replaced by the joy of publishing. But I will take some time to rule this possibility in/out.

The question to start from something is:

can in principle, in this format y[n] ~ normal(x[n] * a, sigma) T[??,];

?? be replaced with regression variables T[x[n] * a,] ?

Thanks

8

Think about it this way:

target += normal_lpdf(y[n] | x[n] * a, sigma) 
  + normal_cdf(x[n] * a | x[n] * a, sigma);

Sampler provides a and sigma, you provide x and y. It’s a density and life goes on. I don’t think this holds as a good model for the lower end of your tail so I doubt it will work but I always have to plot more.