I am replicating the model introduced in this paper, which uses item-response theory to indirectly estimate support for militant groups in Pakistan by a so-called endorsement experiment. Specifically, I am following the simpler model described in section 4.1. I am also using the paper’s replication data, which includes several JAGS models. I am attaching the relevant one for convenience.
ModelSimulationsDivision.txt (1.9 KB)
I have translated their model into Stan.
data {
int<lower=1>
N, // number of respondents
J, // number of questions
K, // number of political actors (not including control group)
D, // number of divisions
P; // number of provinces
int<lower=2> L; // number of choices for each response (5 for Likert scale)
array[N, J] int<lower=1, upper=L> Y; // Y_{ij}
array[N, J] int<lower=0, upper=K> T; // T_{ij}
array[N] int<lower=1, upper=D> division;
array[D] int<lower=1, upper=P> province; // division -> province
}
transformed data {
int treated = 0;
for (i in 1:N) for (j in 1:J)
if (T[i, j] > 0) treated += 1;
int control = N * J - treated;
// For all (i, j) pairs not in a treatment group, a unique index. (0 otherwise)
array[N, J] int treated_index;
{
int idx = 1;
for (i in 1:N) for (j in 1:J)
if (T[i, j] > 0) {
treated_index[i, j] = idx;
idx += 1;
} else
treated_index[i, j] = 0;
}
}
// Translation of ModelSimulationsDivision.txt in the original paper supplement to Stan
parameters {
vector[N] x;
vector[D] delta; // AKA "delta.division"
/* Note: s_{ij0} = 0, i.e. s is zero wherever respondent i,
* question j was assigned to the control group, (endorser number zero).
* So we only parametrize s over the treated (i, j) pairs */
vector[treated] s_treated;
array[K, D] real lambda;
vector<lower=0, upper=10>[K] omega;
vector[P] mu; // AKA "delta.province"
vector<lower=0, upper=10>[P] sigma;
array[K, P] real theta;
array[J] ordered[L - 1] alpha; // \alpha_{jl} increases across l: alpha[j, 1] < alpha[j, 2] < ...
vector<lower=0>[J] beta;
array[K, P] real<lower=0, upper=10> phi;
}
model {
x ~ normal(delta[division], 1);
for (i in 1:N) {
int div = division[i];
real x_i = x[i];
for (j in 1:J) {
int endorser = T[i, j];
if (endorser > 0)
s_treated[treated_index[i, j]] ~ normal(lambda[endorser, div], omega[endorser]);
// s_{ij0} = 0
real s = (endorser > 0) ? s_treated[treated_index[i, j]] : 0;
/* It can be shown that the model given in equation (4) of the paper
* is equivalent to Stan's built-in ordered probit model
* (https://mc-stan.org/docs/functions-reference/bounded_discrete_distributions.html#ordered-probit-distribution),
* assuming that the epsilon stochastic error terms are i.i.d. Normal(0, 1).
* Note that the above link uses k where we use l.
*/
real eta = beta[j] * (x_i + s);
Y[i, j] ~ ordered_probit(eta, alpha[j]); // c := \alpha_j
}
}
beta ~ lognormal(0, 1);
for (j in 1:J) alpha[j] ~ normal(0, 10);
delta ~ normal(mu[province], sigma[province]);
mu ~ normal(0, 10);
for (k in 1:K) {
lambda[k] ~ normal(theta[k, province], phi[k, province]);
theta[k] ~ normal(0, 10);
}
}
Note that their model increases K by one, counting the control group as well. Additionally, they set the first element each (corresponding to the control group) of the lambda, theta, and omega parameters to zero, whereas I omit that index entirely and case on the control/treatment group before using them. This requires a different parametrization of the s matrix to skip over all the indices (i, j) for which the treatment T_{ij} = 1. (I initially just put a soft \text{Normal}(0, 0.0001) constraint on the first values of lambda, theta, and omega, but halving the size of s also makes the model much faster.) They also hand-code the distribution statement for Y[i, j] using an auxiliary p matrix; I switched to Stan’s builtin ordered_probit distribution after confirming doing so would be mathematical equivalent. Lastly, I drop all the provinces with zero interviewees so that there aren’t any delta parameters with no information.
Here are my results as an .Rdata file
However, I get \hat{R} values greater than 3 for some parameters, including all elements of omega, the standard deviation hyperparameter for s. (This was especially true before I boosted adapt_delta to 0.99.) I know that JAGS uses the relatively unreliable Gibbs sampler, but isn’t that supposed to be for underreporting divergences? I get relatively few divergences now but high rhat, low ESS, and warnings about BFMI.
0.0761141 per iter (2025-07-27 06:10:24.33535)
# A tibble: 15,611 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 alpha[2,3] -0.510 -0.550 0.510 0.380 -1.31 0.503 3.11 4.55 11.6
2 alpha[3,4] 0.819 0.795 0.405 0.302 0.193 1.66 3.08 4.55 11.2
3 alpha[2,4] 1.04 0.949 0.519 0.447 0.240 2.08 3.07 4.56 11.2
4 delta[4] 0.460 0.457 0.341 0.255 -0.0840 1.14 3.06 4.56 11.4
5 delta[5] -0.0281 -0.0408 0.337 0.248 -0.552 0.678 3.05 4.56 11.5
6 alpha[3,3] -0.405 -0.468 0.406 0.335 -1.04 0.421 3.05 4.56 11.5
7 delta[11] 0.0588 0.0332 0.368 0.378 -0.530 0.722 3.03 4.57 10.9
8 delta[8] 0.612 0.595 0.357 0.345 0.0568 1.31 3.00 4.58 11.3
9 delta[9] -0.308 -0.344 0.358 0.348 -0.880 0.367 2.99 4.59 11.0
10 delta[10] -0.190 -0.181 0.351 0.305 -0.733 0.509 2.97 4.59 11.0
# ℹ 15,601 more rows
# ℹ Use `print(n = ...)` to see more rows
Warning messages:
1: There were 57 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them.
2: There were 1046 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 10. See
https://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded
3: There were 4 chains where the estimated Bayesian Fraction of Missing Information was low. See
https://mc-stan.org/misc/warnings.html#bfmi-low
4: Examine the pairs() plot to diagnose sampling problems
5: The largest R-hat is 3.1, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat
6: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess
7: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess
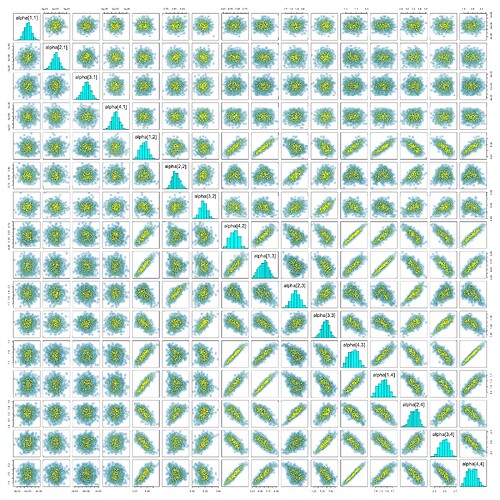
Some pairs plots:
R driver code:
rm(list = ls())
# Replicate the first experiment from the Bullock, Imai, and Shapiro paper
# but using Stan instead of JAGS
library(endorse)
library(dplyr)
library(rstan)
library(posterior)
df <- pakistan
stopifnot(nrow(df) == 5212)
seed <- 1
set.seed(seed)
# a: control
# b: militant groups in Kashmir
# c: militant groups in Afghanistan
# d: Al-Qaeda
# e: Firqavarana Tanzeems
groups <- c("a", "b", "c", "d", "e")
qs <- c("Polio", "FCR", "Durand", "Curriculum")
endorser <- list()
for (q in qs) {
cols <- sapply(groups, \(g) paste0(q, ".", g))
df[[q]] <- do.call(coalesce, df[, cols])
stopifnot(!anyNA(df[[q]]))
endorser[[q]] <- as.matrix(!is.na(df[, cols])) %*% (0:4)
stopifnot(!anyNA(endorser[[q]]))
}
endorser <- data.frame(endorser)
# division -> province
province <- c(rep.int(1, 8), rep.int(2, 5), rep.int(3, 7), rep.int(4, 6))
# Recode the divisions so that there aren't any missing divisions
bij <- sort(unique(df$division)) # new to old bijection
bij_inv <- match(1:26, bij) # old to new
data <- list(
N = nrow(df), J = length(qs), K = length(groups) - 1, D = length(bij), P = 4, L = 5,
Y = df[, qs],
T = endorser,
division = bij_inv[df$division],
province = province[bij]
)
param_counts <- with(data,
list(
x = N, delta = D, s_treated = sum(endorser > 0), lambda = K * D,
omega = K, mu = P, sigma = P, theta = K * P,
alpha = J * (L - 1), beta = J, phi = K * P)) |>
data.frame(row.names = "param_counts") %>%
mutate(total = sum(.))
print(param_counts)
model <- stan_model("pakistan.stan", model_name = "pakistan1")
print("Starting:")
start_time <- Sys.time()
print(start_time)
iter <- 1000
warmup <- 500
fit_ <- sampling(model,
iter = iter,
warmup = warmup,
data = data,
seed = seed,
init = 0,
chains = 4,
cores = 8,
sample_file = "samples",
diagnostic_file = "diagnostic",
refresh = 10,
control = list(adapt_delta = 0.99)
)
end_time <- Sys.time()
elapsed <- difftime(end_time, start_time, units = "mins")[[1]]
cat(sprintf("%.7f per iter (%s)\n", elapsed / iter, toString(end_time)))
ext <- extract(fit_, permuted = FALSE)
summary_ <- summarize_draws(ext)
print(summary_[order(summary_$rhat, decreasing = TRUE), ])
delta_summ <- summary_[startsWith(summary_$variable, "delta"), ]
delta_count <- sapply(1:data$D, \(d) sum(df$division == d))
plot(delta_count, delta_summ$rhat) # or $ess_bulk or $ess_tail
save.image(file = paste0("pakistan.r (", end_time, ").Rdata"))
Thank you for any responses!