The new M4 Apple Silicon chips look to have pretty impressive performance.
Has anyone tried Stan on the an M4 Mac yet?
If so, have you had any technical issues?
Are you getting noteworthy speed ups compared to your old set-up?
The M2 and M3 Macs perform really well for Stan. This is because we’re largely memory bottlenecked in large models and the ARM series is much better at dealing with asynchronous memory access.
I got one of the base-level $500 M4 Mac Minis to play around with – have only run a few Stan models on it so far, but noticing a 1.5-3x speedup relative to my laptop (a 2019 MBP w/ an i9-9980HK), which is consistent with the ~2.5x difference in Geekbench 6 scores. Note also this was using 8 chains in parallel and taking the average across chains (to better reflect the 4p + 6e core composition of the 10c M4 chip).
@jroon @Bob_Carpenter this might also interest you – I did a quick test of within-chain parallelization via reduce_sum in a toy model, comparing my Macbook’s performance to the new M4 Mac Mini’s:
functions {
real partial_sum_lpdf(array[] real y_subset, int start, int end, real mu, real sigma) {
return normal_lpdf(y_subset | mu, sigma);
}
}
data {
int<lower=1> N;
array[N] real y;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(0, 10);
sigma ~ exponential(1);
int grainsize = 1;
target += reduce_sum(partial_sum_lpdf, y, grainsize, mu, sigma);
}
as a sort of empirical “benchmark” of Amdahl’s law (with BF sales, I could get a base M4 Mac Mini for ~$400, so I snagged another 3 and currently have them daisy chained together and to my macbook via TB4 bridge, distributing jobs – including Stan runs – via GNU Parallel. So I can either distribute embarassingly parallelizable runs across all of them, or do eg four independent chains with within-chain parallelization across all 4, or some combination thereof).
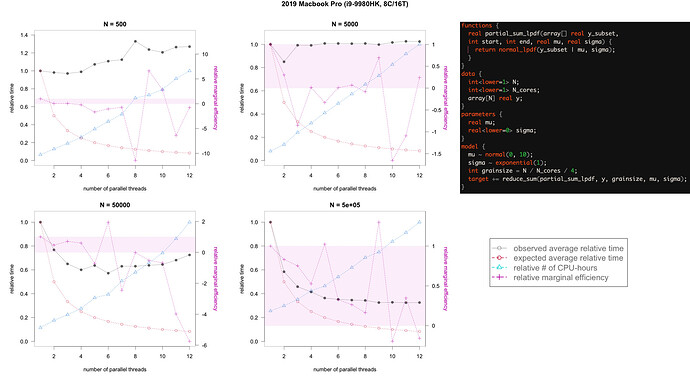
So anyway, I simulate N ∈ {5E2, 5E3, 5E4, 5E5} samples from a normal(2, 1.5) with the same seed and fit the above model with 1, 2, 3, 4… 12 threads, with 50 replicate fits from independent initializations (500 warmup, 500 sampling iterations), using CmdStanR calls to CmdStan. On the MBP I get this scaling:
and on the Mac Mini I get this scaling:
The left axis is in “relative time”, where I divided by the maximum time across 1-12 threads to get everything in (0,1]. So:
Grey closed circles: observed average completion time for a single run (incl warmup), rescaled to a proportion of a single-threaded run
Red open circles: theoretical ideal completion time, just 1 / (1, 2, 3, 4…, 12), with no other bottlenecks (eg i/o)
Blue triangles: relative # of CPU hours using within-chain parallelization, equivalent to the average completion time x the # threads
Pink plusses: Marginal per-thread speed-up of each subsequent thread relative to the theoretical speedup. In other words, the ratio of the differenced grey values to the differenced red values. Axis switches over to the right, and a horizontal pink band marks the [0,1] interval. When near 1, adding a core at the margin improves completion time near the theoretical upper bound. When at 0, adding a core does nothing to speed up the total completion time. When <0, adding a core makes the total completion time go up, worse than doing nothing (the cost of overhead exceeds the cost of more parallel compute). When >1, an average over 50 runs was just too noisy, and the preceding observed average was probably just really bad so the current one probably regressed to (or past) the mean.
Overall, I was curious about a few things:
-
there are benefits to within-chain parallelization in this implementation even with very small models (N=500) – I’d have expected overhead to dominate even at 2 threads.
-
the Mac Mini plateaued at 4 threads – this makes some sense (bc it has 4 performance cores, so maybe once those are used up the efficiency cores can only “pay for themselves” – but I’d still not have expected such exact balance), but it was odd that it did not curve back up, even after 10 threads?
Thanks for the analysis, @NikVetr.
You see this with JAX models, too. It depends on whether your hardware can keep the memory local enough for this to be a win.
I have no idea about the performance vs. efficiency cores, but given what you say, this shouldn’t be too surprising.
Thanks very much for the stats above. The bit I’ve quoted here - I didn’t know this could be done. Do you know any good guides on setting up the TB4 / GNU parallel on multiple apple silicon machines for Stan?
hm, not off the top of my head – the thunderbolt bridge stuff just entailed plugging them all in, going to System Settings > Network > Thunderbolt Bridge, and then Manually configuring them to have the same Subnet mask (I used 255.255.255.0) and different IP addresses (I used 10.0.0.1, 10.0.0.2, 10.0.0.3, 10.0.0.4), and the OS handled the rest. I’m also planning to set up a parallel ethernet network through a 10G/2.5G switch and then only use the thunderbolt bridge to ferry larger files across to prevent whatever minor overhead there is in the daisy-chained communication (eg, I am using tmux + htop to monitor CPU usage across all nodes:
which I have polling every second or so. Additionally, I don’t have admin privileges to my main wifi network, so I used tailscale to set up remote access. At the moment it just looks like this:
For the GNU Parallel stuff, I actually moved away from it 😅 because I couldn’t quite figure out how to get it to survive me shutting down my laptop, or otherwise the node issuing the command restarting etc. So I instead just wrote a few shell scripts implementing my own minimalist job queue system that spawns some specified # of independent workers on each node, which then read from and modify a central queue on the networked drive, logging to job and worker-specific log files and using directory locking to avoid race conditions. So far it’s worked quite well, and I have a good sense of what’s going on under the hood, so it’s easy to modify or extend as needed. But for using GNU parallel any generic tutorial should apply fine, eg: GNU Parallel Tutorial — GNU Parallel 20250122 documentation
Thanks very much thats gives me somewhere to start! In terms of the workflow from the Stan point of view - you are first compiling the Stan program on the main computer and then via the Shell distributing jobs to the worker machines? (i.e. I am assuming you cannot use this distributive computing across machines approach from an interactive Rstudio session… or can you?)
Edit: I managed to set up a cluster without GNU parallel following instructions here for anyone interested: Parallel Workers on Other Machines
That’s a great analysis!
@NikVetr would you mind trying to run this using cmdstan’s across chain sampling? I’d be curious how much sharing the data would help the small and large data models get closer to the peak efficiency
Nice comparison!
A grainsize of 1 is not ideal in this setting. I wonder if one could get better efficiency for the larger sample sizes if one would use some other heuristic here. I’d try a grain size relative to the number of cores and sample size, e.g. to have around 10 chunks of work per CPU. This should reduce the cost of chunking the workload as the Intel TBB (the workhorse under the hood) has a better clue on how to split this up.
No problem! Feel free to ping me if you have any questions, too a bit of trial and error to get everything up and running. :]
you are first compiling the Stan program on the main computer and then via the Shell distributing jobs to the worker machinesA
ah so that’s one hitch I encountered – even though both the hardware and software on the machines is identical (and system paths, up to unique identifiers), I kept getting errors when trying to run a model compiled on one machine on another, so for now I just have them compile each model locally (which takes <1min and needs only happen once across datasets, vs 10-100+ minutes to actually fit the model, so not a huge extra burden)
I am assuming you cannot use this distributive computing across machines approach from an interactive Rstudio session… or can you
I don’t know of any off-the-shelf solutions, but you could just wrap system() calls from R to whatever shell functionality is doing all the work behind the scenes. I’ve been meaning to try to write something to replicate foreach / mclapply type functionality with all the nodes, just haven’t gotten around to it yet. It would be easy enough if you explicitly specify all the dependencies along with the code (to save and transfer all the required data objects in a list, perform the necessary namespace qualification, etc.), but harder if wanting to dynamically identify everything on the fly (but there are lotsa tools to help here, eg codetools::findGlobals, utils:find, pryr::where, etc.)
edit: oh hey, maybe this parallelly package already does all of that, nice find!
So I got it to work off the shelf eventually last night within Rstudio using the parallelly package and the future_apply package (I have a strong preference for the future_xxxxx because you can basically prototype your code with lapply and family commands, and just drop in the future_lapply() etc when you wish to go parallel with minimal extra effort).
So on what worked once I had the ssh stuff set up at the OS level as described here: Parallel Workers on Other Machines, was something like this (missing the actual data/model code here!):
library(parallelly)
library(future.apply)
library(progressr) # to have a progress bar :)
library(rstan)
# set up network worker machines
worker1 <- rep("x.x.x.2", 6) # rep for the numer of cores you want to use on remote machine
worker2 <- rep("x.x.x.3", 6) # rep for the numer of cores you want to use on remote machine
cl_remote1 <- makeClusterPSOCK(worker1,
user = rep("username", 6), # worker1 username
rscript = "/worker1path/Rscript") # remote Rscript path provided here
cl_remote2 <- makeClusterPSOCK(worker2,
user = rep("username", 6), # worker2 username
rscript = "/worker2path/Rscript") # remote Rscript path provided here
# set up on your local machine if you want to use it too
workers_local <- rep("localhost", 10)
cl_local <- makeClusterPSOCK(workers_local)
# combine all workers
cl <- c(cl_local, cl_remote1, cl_remote2)
# lets say you have M datasets to fit stan to
M <- 200
# sim M datasets
### now future apply stuff
plan(cluster, workers = cl)
### progress bar setup
handlers("progress")
with_progress({
p <- progressor(along = 1:M)
# ok fit models with future_lapply()
models_list <- future_lapply(1:M, function(i){
# fit the model
# update the progress update
p(sprintf("i=%g", i))
# return your fit models
return(models_list)
}, future.seed = TRUE) # check future_lapply() help file for details of future.seed
})
plan("sequential") # stop using the workers
N.B. - it wasn’t working for a long time for me becuase I lacked the rscript argument to makeClusterPSOCK(). By default it assumes workers use the same path to Rscript as your local machine - but for me thats not true. (Took me about 2 hours to figure this out, I wish parallelly put this in their example!!)
Also if you set up a .ssh/config file somehow you can avoid passing the worker usernames etc… I just didnt’ get to that yet.
In terms of the workers I didn’t need to pass any variables or anything, I just needed to make sure they had the relevant R packages installed in their R environment which was a do once task!
hm good point. The Stan User’s guide says
The rational for choosing a sensible
grainsizeis based on balancing the overhead implied by creating many small tasks versus creating fewer large tasks which limits the potential parallelism.In
reduce_sum,grainsizeis a recommendation on how to partition the work in the partial sum into smaller pieces. Agrainsizeof 1 leaves this entirely up to the internal scheduler and should be chosen if no benchmarking of other grainsizes is done. Ideally this will be efficient, but there are no guarantees.In order to figure out an optimal
grainsize, if there areNterms andMcores, run a quick test model withgrainsizeset roughly toN / M. Record the time, cut thegrainsizein half, and run the test again. Repeat this iteratively until the model runtime begins to increase. This is a suitablegrainsizefor the model, because this ensures the caculations can be carried out with the most parallelism without losing too much efficiency.For instance, in a model with
N=10000andM = 4, start withgrainsize = 2500, and sequentially trygrainsize = 1250,grainsize = 625, etc., etc.It is important to repeat this process until performance gets worse. It is possible after many halvings nothing happens, but there might still be a smaller
grainsizethat performs better. Even if a sum has many tens of thousands of terms, depending on the internal calculations, agrainsizeof thirty or forty or smaller might be the best, and it is difficult to predict this behavior. Without doing these halvings until performance actually gets worse, it is easy to miss this.
So I was just leaving it at 1 to not do any more intensive benchmarking.
I tried it again setting grainsize to
int grainsize = N / N_cores / 4;
where N_cores is what I set for threads_per_chain in the model$sample() call in cmdstanr, and then reran my earlier script on the i9 MacBook to get:
and on the M4 Mac Mini:
with points here being the average of 50 replicate chains (still a lot of sample variance though given how the curves swing around! also note that these were all fit to the same data).
Focusing on the Mac Mini results, when grainsize=1 before, we had a pretty sharp drop in efficiency going from 4 → 5 cores at high N (5E4, 5E5) and a more gradual drop going with increasing # of cores at low N (5E2, 5E3). With the larger grainsize, it looks like at high N going from 1 to 4 and then from 4 to 5 cores does improve performance, and actually gives an “outsized” jump in performance going from 4 to 5 cores, almost double what it should give? And then a big drop in performance going from 5 to 6 cores? And then at low N yields almost no improvement across the board. I can only assume this has something to do with the 4 performance and 6 efficiency core thing, and how they interact with system memory, but no idea what’s going on past that 😅
Sure, happy to! Though I’m not sure what that actually is. I assume it’s the functionality described in this thread? Cross-chain warmup adaptation using MPI (though sampling suggests it’s not just about fancy pooling during adaptation?)
I have Open MPI installed – do you know if the workflow has been updated any from the above, or would I still want to eg manually add flags in make/local and such?
Oh my. I’m just realizing we never wrote about this feature in our docs and I need to do that.
When running sampling for nuts directly from cmdstan (and pycmdstan) there are command line options for num_chains and num_threads. Setting num_chains=N and num_threads=M will run N chains where all chains run in parallel with access to the M threads. Since all chains share a thread pool in cmdstan you can have multiple chains running in parallel which also use multi threading within the chains. Here is an example setting the chains and threads arguments
./examples/bernoulli/bernoulli sample num_chains=4 data file="./examples/bernoulli/bernoulli.data.R" num_threads=4
The main benefit is that all of the data between the chains is shared so it reduces a lot of memory pressure.
We did:
https://mc-stan.org/docs/cmdstan-guide/parallelization.html#running
https://mc-stan.org/docs/cmdstan-guide/mcmc_config.html#sampler-num-chains
That was me experimenting an idea, and I stopped working on it mainly because:
- The gain comes from a heuristic concept and an ad hoc setting that I was not able to generalize.
- The MPI design is not compatible with existing multi-threading design. At least it requires a major rewrite, with an unclear ROI.