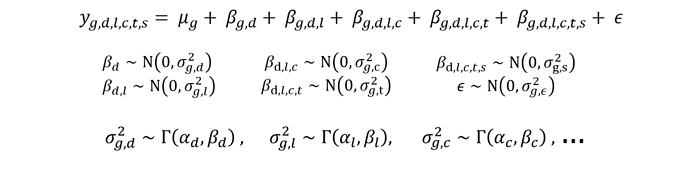I’m trying to fit a linear mixed model of the form attached to some data across multiple genes, g:
I’ve managed to do this without the gamma hyperpriors by fitting separately for each gene with brms.
However, I’d now like to make the model hierarchical across all genes by now incorporating the gamma priors across all genes, where the gamma hyperparameters have noninformative hyperpriors.
I’ve been looking at the Stan code generated by brms in the hope that I could use rstan to fit this model or preferably brms (using something like what has been suggested here ).
My attempt with brms. The problem I’m having here is that the parameter estimates I get back are the sigmas across all genes. I’m hoping to get sigma estimates per gene.
bprior <- set_prior("gamma(alpha_d, beta_d)", class = "sd",group="d:g") +
set_prior("gamma(alpha_l, beta_l)", class = "sd",group="l:d:g") +
set_prior("gamma(alpha_c, beta_c)", class = "sd",group="c:l:d:g")
set_prior("target += student_t_lpdf(alpha_d | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17) + student_t_lpdf(beta_d | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17);", check = FALSE) +
set_prior("target += student_t_lpdf(alpha_l | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17) + student_t_lpdf(beta_l | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17);", check = FALSE) +
set_prior("target += student_t_lpdf(alpha_c | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17) + student_t_lpdf(beta_c | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17);", check = FALSE)
stanvars <- stanvar(scode = "real<lower=0> alpha_d; real<lower=0> beta_d;
real<lower=0> alpha_l; real<lower=0> beta_l;
real<lower=0> alpha_c; real<lower=0> beta_c;", block = "parameters")
model = brm(value ~ 1+(1|g) + (1|d:g) +
(1|l:d:g) +
(1|c:l:d:g) +
(1|t:c:l:d:g) +
(1|s:d:c:l:d:g),
sim_data,cores=ncores,iter=niters,
chains=nchains,silent = TRUE,refresh=0,prior = bprior,stanvars = stanvars)
My attempt in Stan. The problem I’m having here is that the estimates for the beta hyperprior parameters seem to be wild (e.g. 2.238115e+22).
```
data {
int<lower=1> N; // number of observations
vector[N] Y; // response variable
// data for group-level effects of ID 1
int<lower=1> N_1;
int<lower=1> M_1;
int<lower=1> J_1[N];
vector[N] Z_1_1;
// data for group-level effects of ID 2
int<lower=1> N_2;
int<lower=1> M_2;
int<lower=1> J_2[N];
vector[N] Z_2_1;
// data for group-level effects of ID 3
int<lower=1> N_3;
int<lower=1> M_3;
int<lower=1> J_3[N];
vector[N] Z_3_1;
// data for group-level effects of ID 4
int<lower=1> N_4;
int<lower=1> M_4;
int<lower=1> J_4[N];
vector[N] Z_4_1;
// data for group-level effects of ID 5
int<lower=1> N_5;
int<lower=1> M_5;
int<lower=1> J_5[N];
vector[N] Z_5_1;
int prior_only; // should the likelihood be ignored?
}
transformed data {
}
parameters {
real temp_Intercept; // temporary intercept
real<lower=0> sigma; // residual SD
vector<lower=0>[M_1] sd_1; // group-level standard deviations
vector[N_1] z_1[M_1]; // unscaled group-level effects
vector<lower=0>[M_2] sd_2; // group-level standard deviations
vector[N_2] z_2[M_2]; // unscaled group-level effects
vector<lower=0>[M_3] sd_3; // group-level standard deviations
vector[N_3] z_3[M_3]; // unscaled group-level effects
vector<lower=0>[M_4] sd_4; // group-level standard deviations
vector[N_4] z_4[M_4]; // unscaled group-level effects
vector<lower=0>[M_5] sd_5; // group-level standard deviations
vector[N_5] z_5[M_5]; // unscaled group-level effects
//hyperpriors
real<lower=0> alpha_1;
real<lower=0> beta_1;
real<lower=0> alpha_2;
real<lower=0> beta_2;
real<lower=0> alpha_3;
real<lower=0> beta_3;
real<lower=0> alpha_4;
real<lower=0> beta_4;
real<lower=0> alpha_5;
real<lower=0> beta_5;
}
transformed parameters {
// group-level effects
vector[N_1] r_1_1 = (sd_1[1] * (z_1[1]));
// group-level effects
vector[N_2] r_2_1 = (sd_2[1] * (z_2[1]));
// group-level effects
vector[N_3] r_3_1 = (sd_3[1] * (z_3[1]));
// group-level effects
vector[N_4] r_4_1 = (sd_4[1] * (z_4[1]));
// group-level effects
vector[N_5] r_5_1 = (sd_5[1] * (z_5[1]));
}
model {
vector[N] mu = temp_Intercept + rep_vector(0, N);
for (n in 1:N) {
mu[n] += r_1_1[J_1[n]] * Z_1_1[n] + r_2_1[J_2[n]] * Z_2_1[n] + r_3_1[J_3[n]] * Z_3_1[n] + r_4_1[J_4[n]] * Z_4_1[n] + r_5_1[J_5[n]] * Z_5_1[n];
}
// priors including all constants
target += student_t_lpdf(temp_Intercept | 3, -6, 17);
target += student_t_lpdf(sigma | 3, 0, 17)
- 1 * student_t_lccdf(0 | 3, 0, 17);
target+= gamma_lpdf(sd_1|alpha_1,beta_1);
target+= gamma_lpdf(sd_2|alpha_2,beta_2);
target+= gamma_lpdf(sd_3|alpha_3,beta_3);
target+= gamma_lpdf(sd_4|alpha_4,beta_4);
target+= gamma_lpdf(sd_5|alpha_5,beta_5);
target += normal_lpdf(z_1[1] | 0, 1);
target += normal_lpdf(z_2[1] | 0, 1);
target += normal_lpdf(z_3[1] | 0, 1);
target += normal_lpdf(z_4[1] | 0, 1);
target += normal_lpdf(z_5[1] | 0, 1);
// likelihood including all constants
if (!prior_only) {
target += normal_lpdf(Y | mu, sigma);
}
}
generated quantities {
// actual population-level intercept
real b_Intercept = temp_Intercept;
}
```
I am very new to brms/Stan and so am not very confident I’ve done the right thing in either case. Any help on how to approach this would be much appreciated!! Let me know if any more information is needed.
Please also provide the following information in addition to your question:
- Operating System: Windows 10 Pro
- brms Version: 2.8.0