Spatial data with 'highways'

Modeling
1

Hi all,

I’m not sure where this question fits in. I am trying to find a model to capture a very specific scenario.
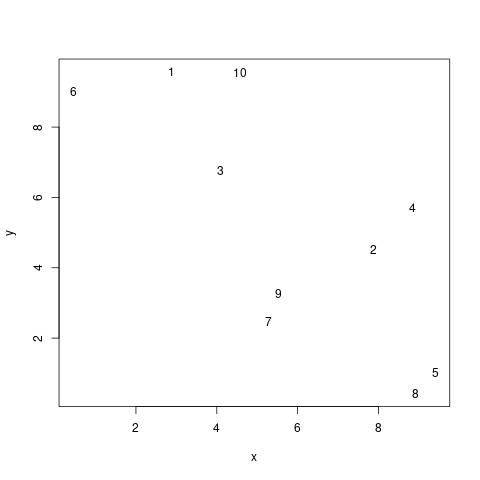
I have data which I assume are spatially correlated. Something like in the following plot:

example

Assuming I’m predicting a gaussian outcome, I would normally do something like:

brm(y ~ 1 + gp(x, y) ...)

To account for the spatial correlation. However, I know that there is a highway (in this case a river) which is connecting 6, 3, 2, and 4.

(1) In the simplest scenario, I would like to be able to account for a higher rate of contact (is that the right word?) between the observations on the highway than between the rest of observations.
In a way, the model should know that the distance between 6, 3, 2, and 4 is reduced.

(2) In the more complex scenario, I would also like to specify that the highway acts as a barrier, so there is a penalty for crossing it. In this toy example, the distance between 10 and 9 should be larger than it would otherwise be were it not for the highway.

One idea I had was to group the observations into three groups c(1, 10), c(6, 3, 2, 4) and c(7, 9, 5, 8) and then do

brm(y ~ 1 + gp(x, y, by = group) ...)

But if I understand it correctly, this assumes that there is no contact across groups. Additionally, this means I have to manually decide which observations belong to which group. But this isn’t always clear.

Is there any way of doing either (1) or (2) in either brms or directly in Stan?

Thanks!

2

Can you use something like osrm to estimate a distance matrix based on drive times from an actual graph of the highway and interstitial road network?

edit: I forgot that the ‘highway’ is a river here. So osrm probably wont work. Still some kind of distance matrix might be helpful.

3

Hi. I could get the river distance between two points. However, the riverdistance will always be larger than the euclidean distance. And there is no riverdistance between a point on the river and a point not on the river. There might also be several non-connecting rivers…

Edit: or maybe the river does a big U turn, so two observations will be on the same river, but the river distance is so much larger than the non-river distance, that the river distance plays no role.