Hello all,
Really struggling with what may just be a non-identified model.
This is an SIRD model being applied to Brazil deaths in 2020. The data is included in the Stan model:
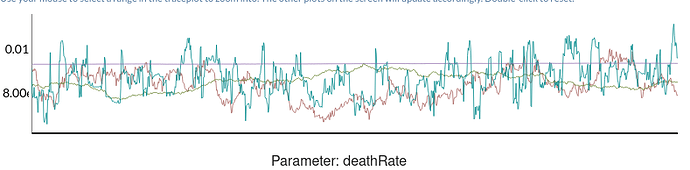
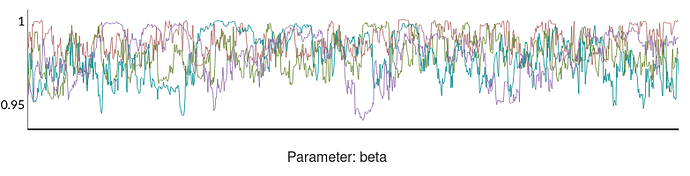
The shinystan output shows poorly mixed chains:
Gamma:
Beta:
DeathRate
Summary has bad Rhats as one might expect:
# A tibble: 5 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta 0.795 0.900 0.173 0.135 0.546 0.987 2.29 5.04 34.4
2 gamma 0.803 0.908 0.173 0.135 0.554 0.995 2.30 5.04 34.9
3 deathRate 0.00863 0.00870 0.000672 0.000797 0.00742 0.00940 1.27 11.8 53.9
4 sigma_deaths_sd 0.0857 0.0856 0.00301 0.00391 0.0821 0.0912 1.23 13.5 129.
5 iDay1_est 2993. 2683. 797. 770. 2124. 4189. 1.76 6.08 32.4
Code to run and graph results:
library(cmdstanr)
library(ggplot2)
library(rstan)
library(tidyr)
library(shinystan)
set_cmdstan_path("/home/breck/.cmdstanr/cmdstan-2.27.0")
model <- cmdstan_model(here::here("stan", "postSIRD.stan"))
fit <- model$sample(data=list(),
parallel_chains = 4,
iter_warmup = 1000,
iter_sampling = 1000,
chains = 4,
seed = 4857)
fit$summary(variables = c('beta', 'gamma', 'deathRate',
'sigma_deaths_sd', 'iDay1_est'))
fit$cmdstan_diagnose()
rstanfit <- rstan::read_stan_csv(fit$output_files())
launch_shinystan(rstanfit)
And finally the relevant Stan code, data is included:
/*
Modified from https://mc-stan.org/users/documentation/case-studies/boarding_school_case_study.html
*/
// include /home/breck/git/codatmo/dataGeneratingProcess1/stan/ode_solvers.stan
functions {
vector sird(real t, vector y, real beta, real gamma, real deathRate, real N) {
real S = y[1];
real I = y[2];
real R = y[3];
real D = y[4];
vector[4] states;
real dS_dt = -beta * I * S / N;
real dI_dt = beta * I * S / N - gamma * I ;
real dR_dt = gamma * I - deathRate * R;
real dD_dt = deathRate * R;
return to_vector({dS_dt, dI_dt, dR_dt, dD_dt});
}
}
data {
}
transformed data {
int<lower=1> n_days = 291;
vector[n_days] deaths =
to_vector({0,1,3,7,11,18,25,34,47,59,77,93,115,139,166,202,244,305,365,445,496,
569,691,826,959,1073,1141,1237,1350,1557,1760,1962,2173,2375,2491,2598,2772,
2940,3349,3722,4074,4301,4606,5092,5534,5980,6438,6810,7073,7381,7972,8597,
9273,10027,10695,11172,11659,12503,13281,14070,14983,15702,16201,16925,18073,
19058,20109,21148,22196,22863,23590,24642,25705,26895,28032,28895,29367,30105,
31473,32667,34152,35253,36054,36530,37393,38586,39824,41092,41935,42792,43426,
44190,45522,46707,47946,49118,50100,50709,51444,52851,53955,55135,56128,57159,
57742,58473,59791,60877,62136,63349,64410,64965,65651,66952,68126,69347,70646,
71578,72195,73030,74324,75602,76902,78026,78870,79578,80346,81663,82959,84272,
85437,86536,87117,87802,89037,90259,91461,92727,93668,94193,94794,96152,97519,
98744,99830,100648,101226,102009,103209,104361,105635,106642,107364,107951,
108747,110099,111263,112499,113551,114378,114834,115551,116760,117839,118824,
119673,120570,120971,121618,122768,123972,124839,125688,126292,126736,127070,
127584,128752,129726,130574,131341,131746,132204,133286,134248,135117,135945,
136626,136977,137443,138237,139169,139964,140786,141508,141845,142238,143096,
143964,144851,145504,146093,146451,146844,147654,148379,149114,149768,150302,
150580,150774,151152,151884,152698,153341,153756,153991,154317,154965,155535,
156041,156604,156991,157192,157526,158052,158556,159107,159680,159972,160175,
160339,160628,161246,161849,162120,162348,162538,162724,162922,163496,164429,
165005,165739,165879,166135,166814,167568,168218,168731,169088,169266,169621,
170248,170870,171581,172140,172684,172917,173268,173953,174630,175393,176070,
176718,177057,177482,178280,179132,179902,180562,181241,181536,182049,182983,
183924,184985,185802,186461,186879,187441,188410,189375,190135,190617,190913,
191250,191788,192839,194056,195072});
int Npop = 214110287;
int<lower = 0, upper = 1> compute_likelihood = 1;
int<lower = 0, upper = 1> scale = 1;
int n_compartments = 4;
int sCompartment = 1;
int iCompartment = 2;
int rCompartment = 3;
int dCompartment = 4;
real ts[n_days];
real meanDeaths = 0;
real sdDeaths = 1;
if (compute_likelihood == 1){
if (scale == 1) {
sdDeaths = sd(deaths);
if (sdDeaths == 0) {
reject("Standard deviation of zero for deaths");
}
}
}
ts[1] = 1.0;
for (i in 2:n_days) {
ts[i] = ts[i - 1] + 1;
}
if (compute_likelihood == 0) {
print("Not running likelihood");
}
}
parameters {
real<lower = 0, upper = 1> gamma;
real<lower=0, upper = 1> beta;
real<lower=0, upper = 1> deathRate;
real<lower=0> sigma_deaths_sd;
real<lower=0> iDay1_est;
}
transformed parameters{
vector[4] y0;
y0[sCompartment] = Npop - iDay1_est;
y0[iCompartment] = iDay1_est;
y0[rCompartment] = 0;
y0[dCompartment] = 0;
real t0 = 0.0;
vector[4] y[n_days] = ode_rk45(sird, y0 , t0, ts, beta, gamma, deathRate, Npop);
}
model {
beta ~ normal(0, 1);
gamma ~ normal(0, 1);
deathRate ~ normal(0, 1);
sigma_deaths_sd ~ normal(0,1);
iDay1_est ~ uniform(0,10000);
if (compute_likelihood == 1) {
for (i in 1:n_days) {
deaths[i]/sdDeaths ~ normal(y[i, dCompartment]/sdDeaths, sigma_deaths_sd);
}
}
}
generated quantities {
real pred_deaths[n_days];
vector[n_days] actual_deaths = deaths;
real D[n_days] = y[, dCompartment];
for (i in 1:n_days) {
pred_deaths[i] =
normal_rng(y[i, dCompartment] / sdDeaths, sigma_deaths_sd) * sdDeaths;
}
}