Hello, there. I am implementing a one-way linear mixed-effects model in rstan.
Y_{ij}=\mu+\sigma (t_i+b_j)+\epsilon_{ij},\quad\epsilon_{ij}\overset{\text{i.i.d.}}{\sim}\mathcal{N}(0,\sigma^2),\quad\text{for }i=1,\dotsb,a;\ j=1,\dotsb,n,
where \mu is the grand mean, t_i is the standardized treatment effects, b_j is the standardized subject-specific random effects, a is the number of levels, n is the number of subjects. Such a statistical model is often used in the within-subject (repeated measures) designs, e.g., Rouder et al. (2012 & 2017).
The priors are
(1) \pi(\mu,\sigma^2)\propto\sigma^{-2} (Jeffreys prior),
(2) t_i\mid g_t\overset{\text{i.i.d.}}{\sim}\mathcal{N}(0,g_t),
(3) g_t\sim\text{Scale-inv-}\chi^2(1,h_t^2),
(4) b_j\mid g_b\overset{\text{i.i.d.}}{\sim}\mathcal{N}(0,g_b),
(5) g_b\sim\text{Scale-inv-}\chi^2(1,h_b^2).
And, one effect is independent of another. The marginal prior for b_j's (or t_i's) is multivariate Cauchy.
My current working Stan model file is
data {
int<lower=1> N; // number of subjects
int<lower=2> C; // number of conditions
vector[C] Y[N]; // responses
real<lower=0> ht; // scale parameter of the standardized treatment effects
real<lower=0> hb; // scale parameter of the standardized subject-specific random effects
}
parameters {
real mu; // grand mean
real<lower=0> sigma; // standard deviation of the error
real<lower=0> gt; // variance of the standardized treatment effects
real<lower=0> gb; // variance of the standardized subject-specific random effects
vector[C] t; // standardized treatment effects
vector[N] b; // standardized subject-specific random effects
}
transformed parameters {
real<lower=0> eta; // sd of the treatment effects
real<lower=0> tau; // sd of the subject-specific random effects
eta = sigma * sqrt(gt);
tau = sigma * sqrt(gb);
}
model {
// linear mixed-effects model
for (i in 1:N) {
Y[i] ~ normal(mu + t + b[i], sigma);
}
t ~ normal(0, eta);
b ~ normal(0, tau);
// priors
// mu ~ implicit uniform prior // Jeffreys prior
target += -2* log(sigma); // Jeffreys prior
gt ~ scaled_inv_chi_square(1, ht);
gb ~ scaled_inv_chi_square(1, hb); // Rouder et al. (2012)
}
Plus, the R script (data source) is
mat <- matrix(c(10,6,11,22,16,15,1,12,9,8,
13,8,14,23,18,17,1,15,12,9,
13,8,14,25,20,17,4,17,12,12), ncol = 3,
dimnames = list(paste0("s", c(1:10)),
c("Level1", "Level2", "Level3")))
datlist <- list(Y = mat, C = 3, N = 10, ht = 0.5, hb = 1)
model1 <- rstan::stan_model(file.choose())
mcmc <- rstan::sampling(model1, data = datlist,
pars = c("mu", "sigma"), refresh = 0,
warmup = 200, iter = 2200, chains = 2)
rstan::summary(mcmc)
The code runs without warnings. Eventually, I want to extend the model to a heteroscedastic case, i.e., the error variance \sigma_i^2 is not constant across the different levels of the treatment. Hence, the variable sigma becomes a vector instead of a real number.
data {
int<lower=1> N; // number of subjects
int<lower=2> C; // number of conditions
vector[C] Y[N]; // responses
real<lower=0> ht; // scale parameter of the standardized treatment effects
real<lower=0> hb; // scale parameter of the standardized subject-specific random effects
}
parameters {
real mu; // grand mean
vector<lower=0>[C] sigma; // standard deviations of the error
vector<lower=0>[C] gt; // variances of the standardized treatment effects
real<lower=0> gb; // variance of the standardized subject-specific random effects
vector[C] t; // standardized treatment effects
vector[N] b; // standardized subject-specific random effects
}
transformed parameters {
vector<lower=0>[C] eta; // sds of the treatment effects
real<lower=0> tau; // sd of the subject-specific random effects
real<lower=0> sigma_pooled; // pooled sd of the error (geometric mean)
sigma_pooled = exp(sum(log(sigma))/C);
eta = sigma_pooled * sqrt(gt);
tau = sigma_pooled * sqrt(gb);
}
model {
// linear mixed-effects model
for (i in 1:N) {
Y[i] ~ normal(mu + t + b[i], sigma);
}
t ~ normal(0, eta);
b ~ normal(0, tau);
// priors
// mu ~ implicit uniform prior // Jeffreys prior
target += -2* log(sigma_pooled); // Jeffreys prior
gt ~ scaled_inv_chi_square(1, ht);
gb ~ scaled_inv_chi_square(1, hb); // Rouder et al. (2012)
}
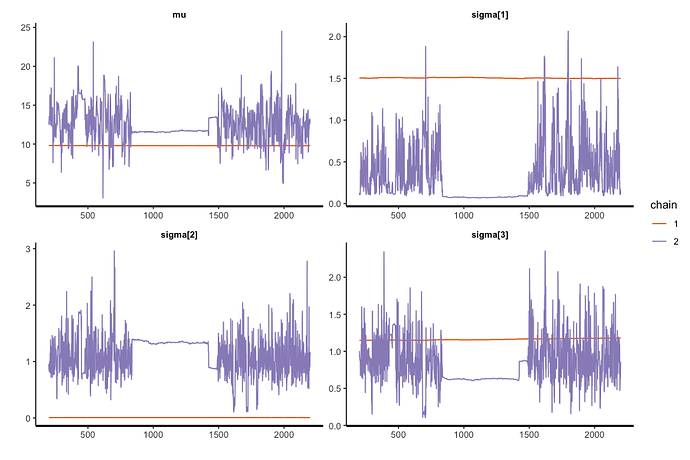
Ideally, the new code should conduct the same work as the previous one in a case of homoscedasticity. However, the console presents some warnings such as “There were 178 divergent transitions after warmup.”.
Any comments on this modeling issue are much appreciated. Thanks.