I am trying to model some data that is Poisson-Binomially distributed. The Poisson-Binomial distribution was discussed here and there is a great implementation for Stan in that thread that was written by Bob Carpenter (thanks!), which I am using.
As I’ve written the model I am getting very poor coverage on simulated data. I am unclear on whether this is because 1.) what I am trying to do is impossible or 2.) the way I’m trying to do it is wrong. So I’ll describe the problem I’m trying to solve in case any of you have some better ideas about how to model it. The problem I’m working on is historical financial data (19th c.) so the data is limited in particular ways and certain gaps cannot be filled in.
The problem
I have a sample of stocks (index i), and each stock falls into a group (index g). There is a binary outcome associated with each stock that I want to model. Let’s call this outcome y_{ig}^* \in \{0,1\}.
For each stock I observe some characteristics that I think should predict the outcome: x_{ig}. In fact, lets stipulate that
where g() is a link function like logit or probit (I try both). So far so straightforward.
Here comes the twist: I mostly don’t observe y_{ig}^*, instead what I observe is y_g = \sum_{i \in g} y_{ig}^*. In words, I don’t observe the binary outcome, instead I observe the sum of these outcomes within each group. I say mostly because for a subset of the data (~30%) I do observe the outcome y_{ig}^* but only for stocks where y_{ig}^*=0.
Thus what I am observing is the sum of independent but not identically distributed bernoulli trials, and this is the definition of the Poisson-Binomial distribution. So I have
where N_g is the number of observations in group g. What I have been doing so far is treating observations I know the outcome for as groups of size 1, so for those observations the model collapses to a standard logit/probit.
Stan code
So the model in stan looks like
//
// This Stan program implements a poisson binomial
// regression where the probability vector is
// parameterized as a logit. The object is to
// recover the logit coefficients
// I use a poisson_binomial_lpmf function taken from the
// Stan forums, see: https://discourse.mc-stan.org/t/poisson-binomial-distribution-any-existing-stan-implementation/
functions {
/**
* Return the Poisson-binomial log probability mass for the specified
* count y and vector of probabilities theta. The result is the log
* probability of y successes in N = size(theta) independent
* trials with probabilities of success theta[1], ..., theta[N].
*
* See: https://en.wikipedia.org/wiki/Poisson_binomial_distribution
*
* @param y number of successes
* @param theta vector of probabilities
* @return Poisson-binomial log probability mass
*/
real poisson_binomial_lpmf(int y, vector theta) {
int N = rows(theta);
matrix[N + 1, N + 1] alpha;
vector[N] log_theta = log(theta);
vector[N] log1m_theta = log1m(theta);
if (y < 0 || y > N)
reject("poisson binomial variate y out of range, y = ", y,
" N = ", N);
for (n in 1:N)
if (theta[n] < 0 || theta[n] > 1)
reject("poisson binomial parameter out of range,",
" theta[", n, "] =", theta[n]);
if (N == 0)
return y == 0 ? 0 : negative_infinity();
// dynamic programming with cells
// alpha[n + 1, tot + 1] = log prob of tot successes in first n trials
alpha[1, 1] = 0;
for (n in 1:N) {
// tot = 0
alpha[n + 1, 1] = alpha[n, 1] + log1m_theta[n];
// 0 < tot < n
for (tot in 1:min(y, n - 1))
alpha[n + 1, tot + 1]
= log_sum_exp(alpha[n, tot] + log_theta[n],
alpha[n, tot + 1] + log1m_theta[n]);
// tot = n
if (n > y) continue;
alpha[n + 1, n + 1] = alpha[n, n] + log_theta[n];
}
return alpha[N + 1, y + 1];
}
}
data {
int<lower=0> N; // N obs
int<lower=0> K; // N covariates
int<lower=0> G; // number of groups
int<lower=0> y[G]; //
matrix[N, K] X; // covariates
int<lower=1> gsize[G]; // vector of group sizes
}
// The parameters accepted by the model. We
// estimate an intercept and the covariates delta
parameters {
real mu;
vector[K] delta;
}
// Make the probability param
transformed parameters {
vector[N] p; // probability
p = inv_logit(mu + X * delta);
}
// The model to be estimated. We model the output
// 'y' to be poisson-binomially distributed with
// individual probabilities p that are a function of
// the parameters delta and mu
model {
int pos;
pos = 1;
mu ~ std_normal();
delta ~ normal(0,5);
for (g in 1:G) {
target += poisson_binomial_lpmf(y[g] | segment(p, pos, gsize[g]));
pos = pos + gsize[g];
}
}
The structure of the problem is similar to some ecological inference problems, with the advantage of knowing some individual covariate information. I’m not the first to see the link between the poisson-binomial distribution and classical ecological regression problems like voting totals and individual characteristics.[^1] In the Rosenman paper the poisson binomial is approximated with a normal distribution. Others have tried to approximate it with a binomial distribution. Perhaps this is because the problem is otherwise intractable? I tried a normal approximation and it went attrociously (not included) but include a binomial approximation which works generally worse than the main model.
Problems
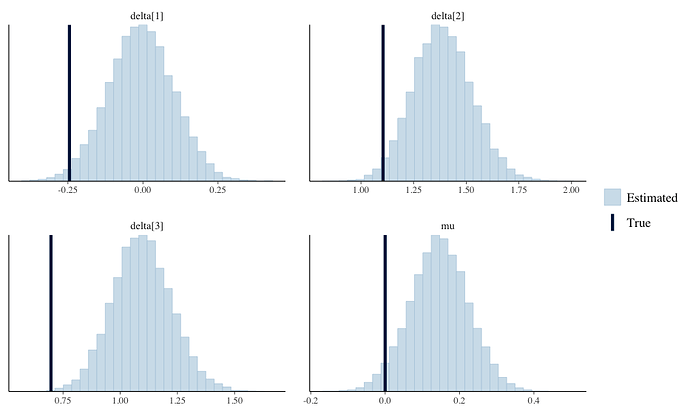
Anyway, what I am finding is that the estimated coefficients are consistently too shrunk towards 0 (the prior) and coverage is poor. The posterior parameter estimates typically appear to be ‘moving in the right direction’ but don’t quite get there. Estimates are rarely terrible, but they’re certainly not great. See for instance this output from the logit model as an example (this is generated from the attached R script):
As you can see the posteriors are all a bit off. In simulation a 95% interval traps the true paramater like ~10% of the time, which is obviously not good.
More promisingly, the estimated probabilities are not atrocious. These are the median estimates of p from the model above:
For these 1000 p parameters, about half of them are putting the true parameter in the central 95% of the posterior distribution. You can see a common pattern here, which is that when p_{ig} is close to 0 or 1 the model shrinks its prediction towards .5 which yields a sort of flipped-sigmoid-curve look.
On the one hand, this is not great. On the other hand, it is much better than the “mean approximation” model I have included as an alternative. For the “mean approximation” model I just average the p_{ig} terms in each group and then estimate a binomial model Y_g \sim Bin(N_g, mean(p_{ig})). This approach is consistently less accurate.
Advice
I’m at a dead-end in terms of ideas about how to improve the model. The probit version of the model is the correct generative model of the simulated data, but the stan code is not recovering the parameters. I’ve tried fiddling the priors, or running the models longer, etc, and haven’t noticed a difference. Perhaps I need to be doing something more with the subsample of the data I observe more fully? I’m not sure how it could be used more aggresively.
Any advice about how to either 1.) improve the approach I’m currently pursuing or 2.) rethinking the problem would be much appreciated. Its unclear to me whether what I am trying to do is feasible: I cannot seem to find discussion of a sort of GLM approach to poisson binomial as I am doing here.
Obviously I would like to perfectly estimate all the parameters, but if that is impossible that I care more about getting p_{ig} well approximated so that I can make smart guesses about y_{ig}^*.
I attach 3 stan programs (logit link function, probit link function, and the mean approximation) and an R script that generates fake data and runs the models. There is also a wrapper function in the R script that can be run to look at coverage but that takes a bunch of time.
Code
discourse_example_poi_bin.R (6.0 KB)
poisson_binomial_logit.stan (2.8 KB)
poisson_binomial_mean_approx.stan (990 Bytes)
poisson_binomial_probit.stan (2.8 KB)
[^1] Rosenman, “Some New Results for Poisson Binomial Models”, Arxiv gives a good overview.