Plotting and validating survival analysis models

[fsdias]

Hi
I’m learning how to fit survival analysis models in Stan. I’m using a dataset that Richard McElreath used in this lecture (minute 31:00): https://www.youtube.com/watch?v=p7g-CgGCS34&list=WL&index=19

This is a dataset of cat adoptions in an animal care facility. The goal is to determine if black cats are less likely to be adopted than other cats.

I’m attaching the dataset and sharing the code I used for this. I already had help from this forum here.

Data preparation:

d <- AustinCats
d$adopt <- ifelse( d$out_event=="Adoption" , 1L , 0L )
dat <- list(
  N=nrow(d),
  days_to_event = as.numeric( d$days_to_event ),
  color_id = ifelse( d$color=="Black" , 1L , 2L ) ,
  adopted = d$adopt
)

Stan model:

data{
int N;
int adopted[N];
vector[N] days_to_event;
int color_id[N];
}
parameters{
vector[2] a;
}
transformed parameters{
vector[N] lambda;
vector[N] mu;
for ( i in 1:N ) {
mu[i] = a[color_id[i]];
mu[i] = exp(mu[i]);
}
for ( i in 1:N ) {
lambda[i] = 1/mu[i];
}
}
model{
a ~ normal( 0 , 1 );
for ( i in 1:N )
if ( adopted[i] == 0 ) target += exponential_lccdf(days_to_event[i] | lambda[i]);
for ( i in 1:N )
if ( adopted[i] == 1 ) days_to_event[i] ~ exponential( lambda[i] );
}
generated quantities{
real pred[N];
for(i in 1:N){
pred[i]=exponential_rng(lambda[i]);
}
}

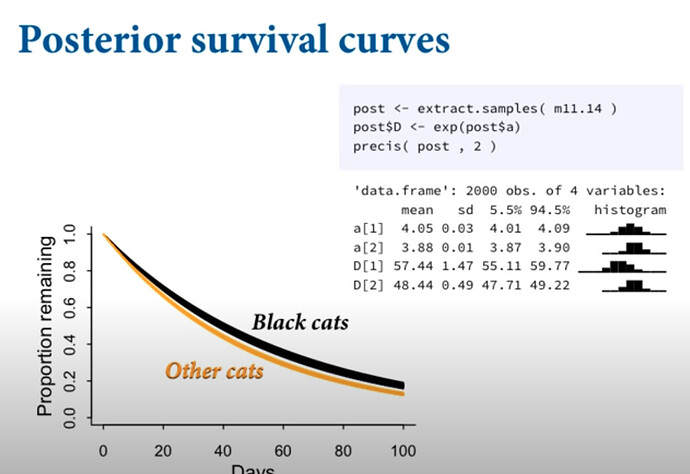
In the slides, Richard McElreath fitted an identical model and plotted it as folllows:

I would like to do two things:

1. learn how to make a similar plot

2. learn how to perform posterior predictive checks so that I can make sure the model fits the data

Can anyone share any hints on how I can do this? Or recommend any resources?

I would like to avoid brms and rstanarm for the time being. I’m trying to learn “pure” Stan.

Thanks

AustinCats.csv (2.8 MB)

[maxbiostat]

@sambrilleman

[fsdias]

I made some progress. I was able to replicate the plot with this code:

post<-rstan::extract(fit)
lambda_black_mean<-1/exp(mean(post$a[,1]))
lambda_black_97.5<-unname(1/exp(quantile(post$a[,1],0.975)))
lambda_black_2.5<-unname(1/exp(quantile(post$a[,1],0.025)))

lambda_other_mean<-1/exp(mean(post$a[,2]))
lambda_other_97.5<-unname(1/exp(quantile(post$a[,2],0.975)))
lambda_other_2.5<-unname(1/exp(quantile(post$a[,2],0.025)))


x=seq(0,100,1)
dat<-data.frame(x=seq(0,100,1),
mean_black=1-pexp(x,lambda_black_mean),
ymin_black=1-pexp(x,lambda_black_97.5),
ymax_black=1-pexp(x,lambda_black_2.5),
mean_other=1-pexp(x,lambda_other_mean),
ymin_other=1-pexp(x,lambda_other_97.5),
ymax_other=1-pexp(x,lambda_other_2.5))

library(ggplot2)
ggplot(dat, aes(x=x, y=mean_black)) + geom_line()+
  geom_ribbon(aes(ymin = ymin_black, ymax = ymax_black),alpha = 1/2)+
  geom_line(aes(x=x, y=mean_other),col="red")+
  geom_ribbon(aes(ymin = ymin_other, ymax = ymax_other),alpha = 1/2)+
  labs(x="days to event",y="Probablity of adoption")

Now, I was wondering if bayesplot has any function for making this type of plot.

Concerning model validation, I also made progress:

days_to_event<-d$days_to_event
pred<-as.matrix(fit,pars=c("pred"))
ppc_dens_overlay(days_to_event,pred[1:500,])

This plot seems to indicate the model doesn’t fit the data very well. Did I do something wrong? Richard McElreath didn’t mention model validation in the lecture, but I’m assuming that he validated the model.

[jonah]

Maybe this new new plot in bayesplot contributed by @fweber144 would be useful?

ppc_km_overlay(): PPC for (right-)censored data

It hasn’t been released on CRAN yet but it’s been merged into the master branch on GitHub so it can be used after installing bayesplot from GitHub.

[fsdias]

Thanks.

library(bayesplot)
days_to_event<-d$days_to_event
pred<-as.matrix(fit,pars=c("pred"))
adopted<-d$adopt
ppc_km_overlay(days_to_event, pred[1:25, ], status_y = adopted)+xlim(0,100)

The code seems to work, but I have two questions:

1. is there a way to make separate curves for black cats and non-black cats? The documentation for ppc_km_overlay() doesn’t mention this, but I was wondering if there is some kind of hack that I can try?

2. is this the right plot to for assessing how well the model fits the data?

[sambrilleman]

Sorry for the late reply (been away for the holiday season), but better late to the party than never I guess.

@fsdias

is there a way to make separate curves for black cats and non-black cats? The documentation for ppc_km_overlay() doesn’t mention this, but I was wondering if there is some kind of hack that I can try?

I’m not familiar with ppc_km_overlay(), so can’t comment on that. But you could take your plot from earlier in the thread – where you plotted the predicted survival curve for each group – and then just overlay the KM estimates for each group by adding a geom_step() to the ggplot object. Something like what we do here in the rstanarm::ps_check() function. But you would add the group variable to the formula in the survival::survfit call so that you get separate KM curves for each group and then extract the group variable from kmfit accordingly and use it as a group in the geom_step() call.

In your setting the psgraph object would be your ggplot from earlier in this thread.

I’m guessing the ppc_km_overlay() function is doing something like that under the hood anyway, although I’m not certain of that since I’ve not seen the code.

@fsdias

1. is this the right plot to for assessing how well the model fits the data?

I guess this plot is checking the overall calibration of the model.

You are probably right to wanna check the calibration by color_id too, which is what you are trying to do in the earlier question.

There are probably a bunch of other checks you could do, things for calibration, prediction error, etc. It would depend how deep you want to go into the validation I guess. @ermeel came up with some pretty cool checks in our StanCon notebook. You could possibly look at that and maybe adopt some ideas if you wanted. I think in rstanarm the only quick check we provide is the plot of KM vs predicted survival like you are doing. Anything more extensive needs to be done somewhat manually using the predictions, kinda like the examples with RMST and Brier score etc in the StanCon notebook I just linked to.

Hope that helps somewhat…

[fsdias]

Thanks @sambrilleman @jonah

I found a package for plotting km curves: https://github.com/michaelway/ggkm and I managed to patch both the km curve and the distribution of predicted values together:

dat_df <- data.frame(
  N=nrow(d),
  days_to_event = as.numeric( d$days_to_event ),
  color_id = ifelse( d$color=="Black" , 1L , 2L ) ,
  adopted = d$adopt
)


post<-extract.samples(fit)
lambda_black_mean<-1/exp(mean(post$a[,1]))
lambda_black_97.5<-unname(1/exp(quantile(post$a[,1],0.975)))
lambda_black_2.5<-unname(1/exp(quantile(post$a[,1],0.025)))

lambda_other_mean<-1/exp(mean(post$a[,2]))
lambda_other_97.5<-unname(1/exp(quantile(post$a[,2],0.975)))
lambda_other_2.5<-unname(1/exp(quantile(post$a[,2],0.025)))

x=seq(0,100,1)
dat_param<-data.frame(x=seq(0,100,1),
                mean_black=1-pexp(x,lambda_black_mean),
                ymin_black=1-pexp(x,lambda_black_97.5),
                ymax_black=1-pexp(x,lambda_black_2.5),
                mean_other=1-pexp(x,lambda_other_mean),
                ymin_other=1-pexp(x,lambda_other_97.5),
                ymax_other=1-pexp(x,lambda_other_2.5))


ggplot(dat_df, aes(time = days_to_event, status = adopted,color=factor(color_id))) + 
  geom_km()+xlim(0,100)+
  geom_ribbon(data=dat_param,aes(x=x, y=mean_black,ymin = ymin_black, ymax = ymax_black),alpha = 1/2, inherit.aes = FALSE)+
  geom_ribbon(data=dat_param,aes(x=x, y=mean_other,ymin = ymin_other, ymax = ymax_other),alpha = 1/2, inherit.aes = FALSE)

Am I correct in concluding the fit is not very good? Or maybe I did something wrong?

[sambrilleman]

@fsdias

I found a package for plotting km curves: GitHub - michaelway/ggkm: Kaplan-Meier plots with at risk table below and I managed to patch both the km curve and the distribution of predicted values together

Awesome!

@fsdias

Am I correct in concluding the fit is not very good? Or maybe I did something wrong?

I’m guessing you did things right, and yeah, the fit is just really poor. It does look like the predicted grey curves are some kind of average of the KM.

The issue is likely that the constant hazard exponential isn’t flexible enough. Try fitting a more flexible model for the baseline hazard – either a parametric model with more parameters, or something like M-splines for the baseline hazard – and then see if that improves thing. Chances are it will – a more flexible baseline hazard will translate to a more flexible shape for the survival curve, so that you are able to catch the “wiggles” in that KM curve shape.

It may also be that the proportional hazards assumption for the two groups isn’t reasonable. But I’d start by using a more flexible baseline hazard (and still assuming proportional hazards) first.

[fsdias]

I spent sometime double checking the plot code. I used “simsurv” to generate data from an exponential distribution, repeated the plotting procedure and it seems to work properly. It seems that it is indeed the fit that’s poor and not my code.

I was thinking about trying a Weibull distribution, but I’m not sure how to formulate the “regression part of the model”. I guess I should write the mean as a function of color_id as I did in the exponential model:

mu=exp(a[color_id])

but I’m a little unsure about the relationship between the Weibull’s parameters alpha and sigma and the mean. The notation on Stan’s manual seems to be different from the one I found on wikipedia. Or maybe I’m missing something. Could you point me to a website/book/paper that clarifies this?

Thanks