Okay, the arguments in this thread have been more difficult to follow than they should have been and that is entirely my fault. Let’s go over some mistakes I’ve made.
Firstly, I’ve provided both code and a picture but I’ve used different names for the same objects. Here’s a quick reference:
P1 = p_sharp_left
P2 = p_sharp_lmiddle
P3 = p_sharp_rmiddle
P4 = p_sharp_right
R1 = rho_left
R2 = rho_right
R3 = rho_subtree
Next, about that picture… it’s supposed to illustrate the new criterion yet depicts a situation where the criterion is redundant and doesn’t even trigger! That’s not helpful, that’s just confusing. Let’s walk through the sampling process step-by-step.
The idea is to build the tree until you find a u-turn. You build a tree with four leapfrog steps. It looks like this:

There is no u-turn here, so you continue and build a second tree. It looks like this:

(Please ignore the fading last node of the first tree, it is not part of this tree.) There is no u-turn here either, so you merge the trees into single big tree. Now the question is, does the big tree have a u-turn? The No-U-Turn criterion we all know and love assumes the tree looks like this:

and tells you: “If the ends of the tree (green) are moving in the general direction of the momenta summed over the whole tree (blue) then there is no u-turn.”
But the tree looks like this:
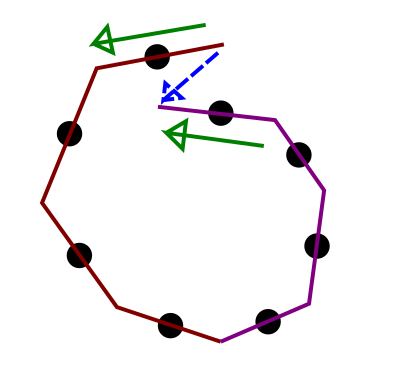
The No-U-Turn criterion gives you the wrong answer.
Reading Betancourt’s posts again made me understand how to think about this in terms of continuous trajectories. The trajectory is continuous but segmented into timesteps and the u-turn condition is checked using the midpoints of the segments, not their boundaries. Suppose the speed and stepsize are such that it takes 14.5 timesteps to go around the great circle once. Once a trajectory is 8 segments long it starts to contract and should be stopped. However, the discretization error effectively chops off half a segment from both ends and makes the actual comparison with points only 7 segments apart. These are still expanding and the trajectory is doubled to 16 segments. The discretization error again removes one segment and we are left with 15 segments. But since that’s more than 14.5 it wraps around and the trajectory is expanding once again. No evidence of a u-turn has been seen. My proposed solution has been to check if the motion during the “skipped segment” in the middle of the trajectory is in fact antiparallel to the total motion between the checked endpoints.
Moving on.
When you file a bug report you should always include a short piece of code that demonstrates the issue. Something which can be found nowhere in my posts. Oops.
import pystan
import pystan.diagnostics
model = pystan.StanModel(model_code="""
data {
int N;
} parameters {
vector[N] x;
} model {
x ~ std_normal();
}""")
fit = model.sampling(data=dict(N=200), chains=20,
control=dict(max_treedepth=12),
refresh=0, check_hmc_diagnostics=False)
pystan.diagnostics.check_treedepth(fit, verbose=3)
WARNING:pystan:24 of 20000 iterations saturated the maximum tree depth of 12 (0.12 %)
WARNING:pystan:Run again with max_treedepth larger than 12 to avoid saturation
I didn’t include rng seed because Stan doesn’t guarantee reproducibility across machines anyway. While the code doesn’t fail every time it does fail often enough that you should have no problem seeing the treedepth warning. You can make the warning happen almost every time by using the default max_treedepth but I wanted the most dramatic example.
The treedepth at which trajectories circle around for this model is 4 because that is what the chains that didn’t blow up have and also what you get with N=500. Those 24 out of 20,000 transitions apparently managed to do 12-4=8 doublings too many which means looping around the origin at least 128 times without noticing a single problem. This is alarming.
And one more thing. I mentioned four alternative new criteria and said that two of them could still miss some u-turns. That was just a guess. Here’s a proper counterexample, a u-turn that the first criterion says isn’t there. (Intermediate points omitted.)
Here R3 and P2 are both downward and even though P3 goes upward it’s so small it has little effect on the average direction at the point where the subtrees join.
It means
(p_sharp_lmiddle + p_sharp_rmiddle).dot(rho_subtree) > 0 and my original proposal would not terminate this trajectory.
Looking at the picture we see that there is no room for P3 to align with R3 without also antialigning with R2 (and violating the u-turn condition on the right subtree). If the lengths of R1 and R2 were reversed we could mirror the image and get the same constraint for P2. So checking if either of p_sharp_lmiddle.dot(rho_subtree) or p_sharp_rmiddle.dot(rho_subtree) is negative is in fact a loophole-free condition, contrary to my guess.
