NB vs. Poisson: LOO and grouped Kfold CV

[jd_c]

Almost always when I work with count data, NB seems to be better than Poisson. But recently I have an interesting problem, where it seems that the Poisson could, oddly, be better. I can’t share the data, but will share the posterior predictive checks, LOO, and grouped K-fold CV results.

I am analyzing an experiment where I have bacteria samples taken from different objects (object). Many experiments (experiment_id) are done for each of many object. For each experiment_id, two control samples are taken, two different treatments applied (experiment_type), and then two post-treatment samples are taken. Thus for each experiment_type there is a matched pair (control and treatment), pair_id. These are ‘within-object’ such that the object serves as it’s own control. The goal is to compare the two treatments.

The model formula is specified like this in brms:

bf(count ~ 1 + treatment + experiment_type + treatment:experiment_type + (1|object/experiment_id/pair_id))

I am interested in the interaction.
My question here is however about NB vs Poisson choice.

I fit one model, m1nb, using family=negbinomial, and one model, m1po, using family=poisson.
The results were very similar, though certainly not the same. Of note, the Poisson model required greater tree_depth and more iter, while the NB model ran fine with defaults on iter and tree_depth.

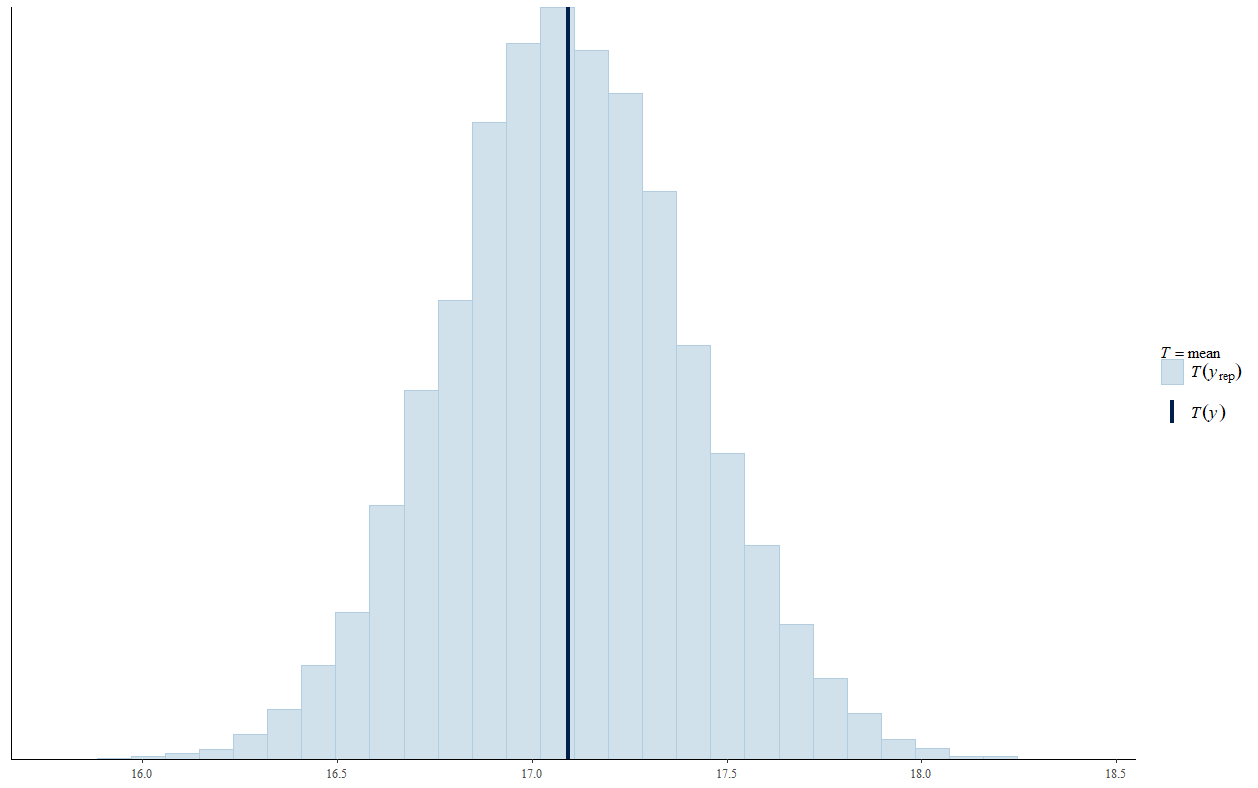
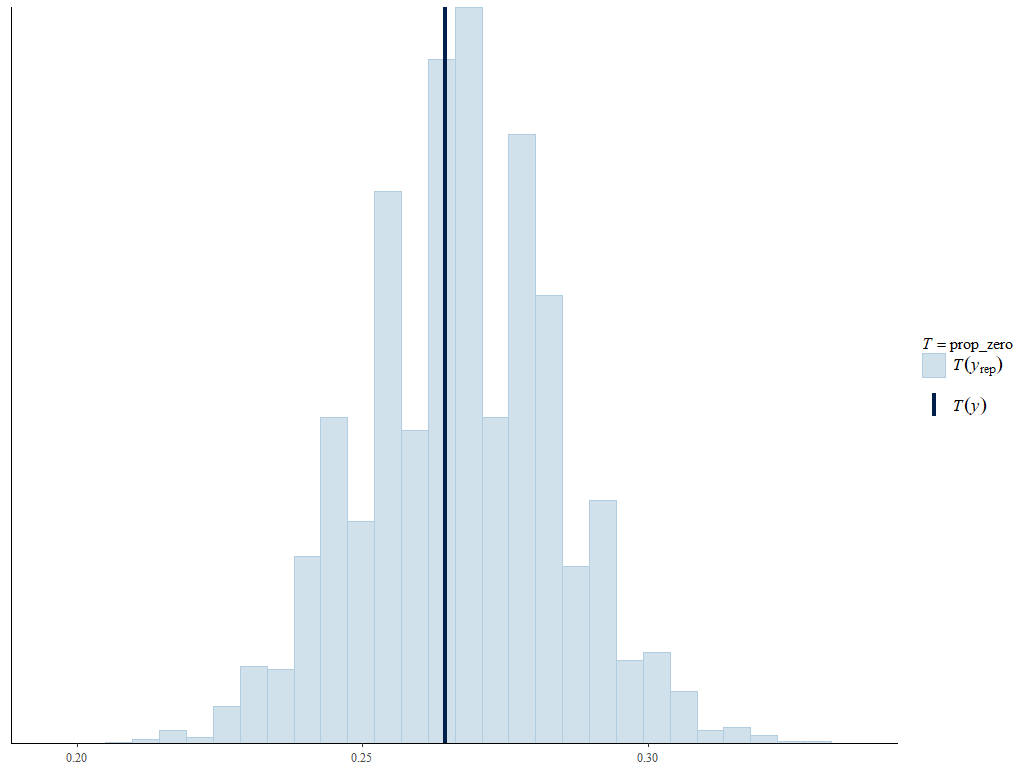
Viewing the posterior predictive checks, the Poisson model looks better.
Poisson:

Negative binomial:

The negative binomial model posterior predictive checks show much higher max counts than seen in the data, and the mean is a little off.

I then ran LOO-CV and obtained these results:

There are many high pareto k’s, especially with the Poisson model. The negative binomial is favored. Referencing the helpful LOO FAQ, I can see that my case here is like the third example in part 16 of the FAQ, where for the Poisson model, p_loo > p and p > N/5, so the posterior predictive checks could be untrustworthy.

Furthermore, thinking about this situation with CV, I think leave-one-out is not what I want with matched pairs, but rather I want ‘leave-pair-out’ CV. Thus I decided to do leave-4 pairs-out K-fold CV, which should be a good estimate. Even leaving four pairs out takes forever to run, as K=44 here. But I run it and obtain these results:

Basically leave-4pairs-out CV is similar for both models, although p_kfold is much higher for the Poisson model, which is I believe due to the varying intercept for pairs acting in place of the dispersion parameter in the NB model. In fact, the estimate for the sd for the varying intercept for pairs in the Poisson model is higher than in the NB model.

As mentioned the results are similar (though certainly not identical) for the two models… I am leaning towards using the results from the NB model, simply based on past experience and the fact the model ran much better and the posterior predictive checks aren’t horrible. I would love for @avehtari or someone else to weigh in on these results. Is there a best model here? If I had to go with one model, which results for inference on the treatment effect should I use?

I was impressed with the difference in LOO and leave-pair-out K-fold CV…I guess not so surprising as they answer different questions, but I will admit being a little surprised.

[Bob_Carpenter]

@jd_c

Furthermore, thinking about this situation with CV, I think leave-one-out is not what I want with matched pairs, but rather I want ‘leave-pair-out’ CV.

You definitely need to be sensitive to groupings for cross-validation. With text, you could cross-validate at the word level or at the sentence level or at the document level, for example. With a hierarchical clinical trial like described in BDA3 chapter 5, you might leave a whole cohort out or leave individual subjects out. With a time series for prediction, you typically leave future observations out. The paper by Gelman, Meng, and Stern has a nice discussion of the same issue for posterior predictive checks, and packages like scikit.learn do a good job of letting you cross-validate by group as well as by item.

Can you leave a pair out with loo by simply taking the log_lik values to be defined over the relevant pairs?

[jd_c]

Thanks! Yes, that is what I thought as well.

@Bob_Carpenter

Can you leave a pair out with loo by simply taking the log_lik values to be defined over the relevant pairs?

I am honestly not sure. Doing the leave pair out was pretty straightforward for the k-fold CV Cross-validation for hierarchical models
It was interesting how different the results were vs LOO.

@Bob_Carpenter

The paper by Gelman, Meng, and Stern has a nice discussion of the same issue for posterior predictive checks,

I’ll have to take a look. Should something different be done in terms of posterior predictive checks? I wasn’t aware of that.

[Bob_Carpenter]

@jd_c

Doing the leave pair out was pretty straightforward for the k-fold CV Cross-validation for hierarchical models

Technically it should work, it’s really just a software question. loo will be a lot faster and you can see if you get basically the same result.

@jd_c

Should something different be done in terms of posterior predictive checks?

I only cited their paper because it discusses individual- vs. group-level validation. Posterior predictive checks are in-sample and cross-validation is out of sample (well, still in your original sample, but not in the “training” data).

[avehtari]

First I want to say that your way to ask the question and provide useful information is great.

@jd_c

The negative binomial model posterior predictive checks show much higher max counts than seen in the data, and the mean is a little off.

The mean (Ty) doesn’t need to be exactly in the middle, and for Poisson the mean being exactly in the middle of ppc results is likely due to the overfitting to the data and the test statistic being far from ancillary. It would be better to use, e.g. max and number of zeros as test statistics. Now you mention much higher counts, but didn’t show the plot with T() being max().

@jd_c

There are many high pareto k’s, especially with the Poisson model. The negative binomial is favored. Referencing the helpful LOO FAQ, I can see that my case here is like the third example in part 16 of the FAQ, where for the Poisson model, p_loo > p and p > N/5, so the posterior predictive checks could be untrustworthy.

See also Roaches cross-validation demo, which resembles your case.

@jd_c

Furthermore, thinking about this situation with CV, I think leave-one-out is not what I want with matched pairs, but rather I want ‘leave-pair-out’ CV.

This makes sense. In theory, you could do this also with PSIS, by summing together log_lik values of the pairs, and then giving the new matrix to loo() function. However, since LOO already was unreliable with many high Pareto k’s, this would be even more unreliable.

@jd_c

Basically leave-4pairs-out CV is similar for both models, although p_kfold is much higher for the Poisson model, which is I believe due to the varying intercept for pairs acting in place of the dispersion parameter in the NB model.

Yes. This also hints that the dispersion distribution is close to gamma (negbin is a gamma-Poisson mixture). You could look at the distribution of the “random effects” in Poisson model and compare that distribution to gamma distribution to check if there is something interesting to see.

@jd_c

I was impressed with the difference in LOO and leave-pair-out K-fold CV…I guess not so surprising as they answer different questions, but I will admit being a little surprised.

I would expect also leave-one-out with K-fold-CV showing similar results that there is not much difference between Poisson and negbin, as the “random effects” can present the same overdispersion as negbin.

@jd_c

I am leaning towards using the results from the NB model, simply based on past experience and the fact the model ran much better and the posterior predictive checks aren’t horrible. I would love for @avehtari or someone else to weigh in on these results. Is there a best model here? If I had to go with one model, which results for inference on the treatment effect should I use?

I would go with negbin due to more stable computation.

@jd_c

(1|object/experiment_id/pair_id)

I would also test what happens if you drop pair_id from here. If the overdispersion over pairs can be modelled with gamma distribution then the performance of the negbin model doesn’t change, but the performance of Poisson model would drop a lot. Compare what happens in Roaches cross-validation demo

[jd_c]

@avehtari

First I want to say that your way to ask the question and provide useful information is great.

Thanks @avehtari!! I try. I appreciate the help so much. Also, can’t believe I missed the Roaches cv demo, as that is pretty similar to what I am doing. I’ll take a look.

@avehtari

It would be better to use, e.g. max and number of zeros as test statistics. Now you mention much higher counts, but didn’t show the plot with T() being max().

Ah ok, will do. Below I show the pp_checks for the proportion of zeros and max value for both the negative binomial and the Poisson.
Proportion of zeroes for negative binomial model:

Proportion of zeroes for the Poisson model:

Max value for the Negative Binomial model:

Max value for the Poisson model:

Interesting. So the NB is better when it comes to predicting the zeroes but worse for the max value. I’m wondering if this hints at the dispersion parameter being estimated a bit low, as it seems maybe it is trying to account for all the zeroes but still capture the mean, which would probably make a low dispersion parameter which also means high max values. Something like zero-inflated-nb might fit a lot better, but I would worry about the interpretation…whenever I have used zinb in the past, I have always thought of 2 separate processes, where one process always results in zeroes. For example, I modeled the bioburden on portable medical equipment using a zinb model, because some equipment is not touched and therefore acquires no bioburden, leading to zero inflation. However, in this experiment there is no process like that. The reason there is a lot of zeroes is that one of the treatments works exceedingly well and reduces the counts to zero in almost all cases…not sure how to think of zinb in a case like this.

@avehtari

I would also test what happens if you drop pair_id from here. If the overdispersion over pairs can be modelled with gamma distribution then the performance of the negbin model doesn’t change, but the performance of Poisson model would drop a lot.

Ok, I tried this and was very surprised that all of the ‘population-level’ parameter estimates were still pretty much the same! In addition, the pp_checks looked pretty good. I had to not only drop pair_id but I also had to drop experiment_id, which I suppose makes sense…still, I thought dropping pair_id would have more effect for the Poisson model, but I think it just used experiment_id like an overdispersion parameter once that happened. Once experiment_id was dropped, the performance of the Poisson became worse in terms of pp_checks.
Here are the pp_checks for the Poisson model when pair_id was removed:

And here are the pp_checks when both pair_id and experiment_id were dropped.

And here I show pp_checks for the NB when both pair_id and experiment_id were dropped.

And here is LOO for all of the models described above (models with “B” have the pair_id dropped and models with “C” have both pair_id and experiment_id dropped). Unfortunately it is too time consuming to run K-fold leave pair out for all of these models.

Finally, I run a zinb model. Here are the pp_checks:

And LOO results comparing to the original NB model:

It takes >24hs to run the leave a pair out K-fold CV, so I didn’t have time to do that.

Contrary to what I predicted above, the zinb doesn’t help. At this point, I think going with the original NB model is the way to go.

[avehtari]

@jd_c

Interesting. So the NB is better when it comes to predicting the zeroes but worse for the max value.

The T(y) line is within the histogram, so you can’t interepret that from that. If you have further information about the feasible maximum values, then you can claim that negbin is predicting too large values.

@jd_c

I had to not only drop pair_id but I also had to drop experiment_id, which I suppose makes sense…still, I thought dropping pair_id would have more effect for the Poisson model, but I think it just used experiment_id like an overdispersion parameter once that happened. Once experiment_id was dropped, the performance of the Poisson became worse in terms of pp_checks.

Ah, I think I did get confused of the role of each of these terms. To clarify, can you clarify the number of levels in each of these factors and does experiment_id have as many levels as there are observations? It seems very much as overparameterized model with all the combinations from object/experiment_id/pair_id if one of these has as many levels as the number of observations.

[jd_c]

@avehtari

Ah, I think I did get confused of the role of each of these terms. To clarify, can you clarify the number of levels in each of these factors and does experiment_id have as many levels as there are observations? It seems very much as overparameterized model with all the combinations from object/experiment_id/pair_id if one of these has as many levels as the number of observations.

Sure! It would be much easier to just share data and results, but unfortunately I can’t. There are 5 levels of object, 86 levels of experiment_id, 172 levels of pair_id, and 344 obs total. This is an experiment where we are testing 2 different treatments on a variety (5) of objects. Each experiment, experiment_id, consists of 4 observations: 2 pairs of control and treatment observations for each of the 2 different treatments. Each single experiment is conducted on the same object, thus it is within-object design, making the two treatments comparable (with assumptions haha). The goal is to compare the difference in the treatment effect (treatment vs control for each pair) between the two types of treatment.
For a linear model, this would be analogous to the linear mixed model or paired T-test in frequentist stats. It has the additional complexity of pairs within experiments and experiments within object types, though. In addition, the outcome is count data (environmental bioburden). While this might seem overly complex, I can assure you that based on much past experience that the variability among objects, among experiments within objects, and even between the pairs within the same experiment on the same object, can be quite high. It wasn’t as high as I have seen in the past, but still there (this from the NB model):

[avehtari]

@jd_c

There are 5 levels of object, 86 levels of experiment_id, 172 levels of pair_id, and 344 obs total.

ok, now it’s clear. Sounds like an interesting analysis,

@jd_c

the variability among objects, among experiments within objects, and even between the pairs within the same experiment on the same object, can be quite high.

I can see that form the results.

@jd_c

And here is LOO for all of the models described above

Based on these I would pick m1nbB as it has practically the same performance as m1nb. Of course it’s good to check the result from leave-pair-out, too

[jd_c]

@avehtari

Based on these I would pick m1nbB as it has practically the same performance as m1nb. Of course it’s good to check the result from leave-pair-out, too

Thanks for all of the input! One question: doesn’t ‘m1nbB’ have the problem of not accounting for the matched pairs though? Since this is a matched pairs design (control matched to treatment in each pair), I would have thought that one would always include the pairs id… similar to how the linear mixed model with a varying intercept for pairs would be analogous to the paired t test. It seems like by design the pairs id should be included…or does it not matter if leave-pair-out CV indicates similar performance and the ‘population-level’ effects are similar?

[avehtari]

@jd_c

One question: doesn’t ‘m1nbB’ have the problem of not accounting for the matched pairs though? Since this is a matched pairs design (control matched to treatment in each pair), I would have thought that one would always include the pairs id… similar to how the linear mixed model with a varying intercept for pairs would be analogous to the paired t test. It seems like by design the pairs id should be included…or does it not matter if leave-pair-out CV indicates similar performance and the ‘population-level’ effects are similar?

That’s a good point. In this case, it seems that the variation between pairs is small, or can be explained by the overdispersion in negbin so that dropping the pair-specific parameter doesn’t affect the other parts of the model that much that it would affect the predictive performance. It is also sensible to include the term, as then you can also directly look at the posterior sd of those terms and the posterior of the terms, directly getting thus more information than from the model that doesn’t include them (given sensible priors, model selection is not needed, and the richest model is the most useful).

If you have time and energy, the roaches example shows how to do integrated LOO, and since you have one parameter per pair, you could also do integrated-leave-pair-out cross-validation with less high khats and faster than K-fold-CV.

[jd_c]

Just as a follow-up for interest, the results for leave-4 pairs-out K-fold CV for the m1nb and m1nbB models are practically the same (other than p_kfold):

@avehtari

can be explained by the overdispersion in negbin so that dropping the pair-specific parameter doesn’t affect the other parts of the model that much that it would affect the predictive performance

This is exactly what happens. The group-level and population-level effects (as called by brms) are very close to identical (with of course no pairs_id sd in m1nbB), but the dispersion parameter is quite a bit lower in the m1nbB model vs the m1nb model.

@avehtari

It is also sensible to include the term, as then you can also directly look at the posterior sd of those terms and the posterior of the terms, directly getting thus more information than from the model that doesn’t include them (given sensible priors, model selection is not needed, and the richest model is the most useful).

I feel a bit more comfortable reporting results for m1nb, simply given the experiment was designed as a matched pairs experiment. Although it does appear unnecessary to keep it.

Thanks again @avehtari for the help! I’ll look into integrated LOO in the future, as this seems like it could be very handy when working with hierarchical models.

[avehtari]

Please share the paper when it’s public!