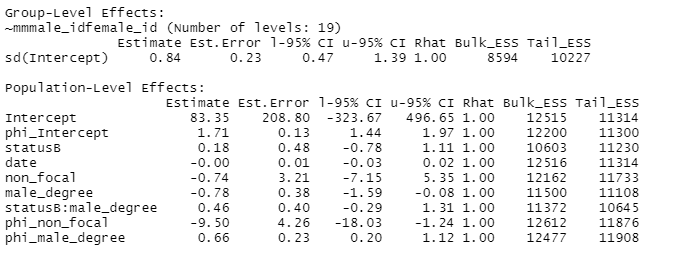
No not quite. A larger phi means less dispersion. A phi closer to zero (some small fraction) means greater dispersion. On the log scale (the output of brms), smaller phi is more negative values and larger phi is more positive values (like, a really small phi might be -5 and a really large 5, since it is log scale). In your example, non-focal contributes to making phi smaller and thus contributes to more dispersion.
If you are modeling phi, and the parameter for some predictor is around zero, then this simply means that the predictor isn’t contributing much to predicting the dispersion parameter. It doesn’t mean that there is no dispersion.
I wrote a simulation with notes, as this might help you understand what is going on. You can easily run the code for yourself. When you simulate data, it makes it explicit how the data generation process works. Notice what phi is actually doing and how it relates to the binomial part of the model.
library(brms)
#Let's program 2 simulations: 1) where phi is very small (close to zero), when phi is really small, there is a large amount of dispersion;
#and 2) when phi is really large, when phi is really large, then there is not much dispersion
#To simulate from beta binomial, you provide a model for mu and phi and then generate p from the beta distribution. Then, you take
#the p that you generated and use it in a binomial distribution to generate the outcome.
#simulation 1, very small phi
#small value for phi, binomial vs beta binomial model
n <- 500 #number of observations
x <- rnorm(n, 0, 1) #predictor x, simply a centered and scaled predictor
mu <- plogis(-1 + 0.5*x) #model for mu, on the logit scale as in brms
phi <- exp(-5 + 0.25*x) #model for phi, on the log scale as in brms
shape1 <- mu * phi #shape 1 for the beta distribution in R
shape2 <- (1 - mu) * phi #shape 2 for the beta distribution in R
p <- rbeta(n, shape1, shape2) #simulate p from beta distribution using shape 1 and shape 2 parameters that we got from our mu and phi models
tr <- rpois(n, lambda=100) #simulate some number of trials for the binomial distribution
y <- rbinom(n, tr, p) #simulate our outcome y from a binomial distribution with our number of trials and our p from the beta distribution
d1 <- cbind.data.frame(y, tr, x) #bind them all in a dataframe
hist(y/tr, breaks=100) #view our outcome as a proportion of outcome y divided by trials. Note this is very dispersed! Most values are near zero or one
#run a binomial and a beta binomial model in brms
m.b <- brm(y | trials(tr) ~ 1 + x, family=binomial, data=d1, cores=4)
m.bb <- brm(bf(y | trials(tr) ~ 1 + x, phi ~ 1 + x), family=beta_binomial, data=d1, cores=4)
m.b
m.bb
#similar values for Intercept and x, which is the mean p on the logit scale
#this can be visualized in posterior predictive checks below, where the mean is similar for both the binomial and the beta binomial models
pp_check(m.b, type='stat')
pp_check(m.bb, type='stat')
#However, since the binomial does not have the dispersion parameter, it cannot model the extreme overdispersion,
#so while the mean is correct, the distribution of p (and thus the y outcome) isn't modeled correctly.
#You can see this in posterior predictive checks with histograms or density plots. The binomial is really bad, but the beta binomial is great.
pp_check(m.b, type='hist')
pp_check(m.bb, type='hist')
pp_check(m.b)
pp_check(m.bb)
#simulation 2, large phi
#now let's look at similar simulation but instead have a large value for phi; binomial vs beta binomial model
n <- 500
x <- rnorm(n, 0, 1)
mu <- plogis(-1 + 0.5*x)
phi <- exp(5 + 0.25*x) #this time we make phi large by making the intercept for phi on the log scale, large and positive
shape1 <- mu * phi
shape2 <- (1 - mu) * phi
p <- rbeta(n, shape1, shape2)
tr <- rpois(n, lambda=100)
y <- rbinom(n, tr, p)
d2 <- cbind.data.frame(y, tr, x)
hist(y/tr, breaks=100) #note this is much less dispersed than the example with small phi
m.b2 <- brm(y | trials(tr) ~ 1 + x, family=binomial, data=d2, cores=4)
m.bb2 <- brm(bf(y | trials(tr) ~ 1 + x, phi ~ 1 + x), family=beta_binomial, data=d2, cores=4)
m.b2
m.bb2
#Again, we have almost the same estimates of Intercept and x for both models, which is the model for the mean
#As expected posterior predictive checks for the mean look similar for both models
pp_check(m.b2, type='stat')
pp_check(m.bb2, type='stat')
#Now let's look at the distribution of the outcome y and compare the two models. Notice that unlike in the first
#example when phi was really small, now the binomial is actually not bad looking. It looks pretty similar to the beta-binomial.
#Why is that? It is because phi is really large, and as phi gets larger and larger, then it approaches the binomial distribution.
pp_check(m.b, type='hist')
pp_check(m.bb, type='hist')
pp_check(m.b2)
pp_check(m.bb2)