Hi all,
I’m hoping to get some pointers that might improve sampling efficiency for a multilevel, binomial logit model I’ve been working on. The current version of the model (below) appears to fit the data well according to comparisons of the ‘n_successes’ observed and the ‘y_new’ detailed in the generated quantities block below. Likewise, the parameters fit closely resemble patterns from a log-normal version of the model I’ve fit previously. In that model, someone else had generated estimates for log-concentrations derived from the raw binomial data. This is digital PCR data.
Here, of course, I’m looking to fit the raw, binomial data; however, the model takes around an hour and a half to fit the N=1850 observations. This is compared to about a minute or less for the log-normal version. Likewise, the sampling appears to less than ideal. Here is a summary from the last run (sorry for formatting: pointers accepted):
Inference for Stan model: stan-45e01a247373.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
b0 -6.84 0.02 0.29 -7.40 -7.03 -6.84 -6.65 -6.28 173 1.02
b1 1.98 0.03 0.24 1.51 1.82 1.97 2.14 2.47 67 1.05
sigma 2.19 0.00 0.04 2.11 2.16 2.18 2.21 2.27 93 1.03
sigma_a[1] 1.36 0.01 0.20 1.02 1.22 1.34 1.48 1.81 255 1.01
sigma_a[2] 0.64 0.02 0.24 0.16 0.49 0.64 0.80 1.15 98 1.02
Omega[1,1] 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.00 2000 NaN
Omega[1,2] -0.29 0.02 0.26 -0.74 -0.47 -0.30 -0.12 0.24 272 1.00
Omega[2,1] -0.29 0.02 0.26 -0.74 -0.47 -0.30 -0.12 0.24 272 1.00
Omega[2,2] 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.00 1995 1.00
lp__ -6473.63 3.99 41.23 -6553.38 -6502.59 -6473.49 -6446.74 -6394.12 107 1.03
Samples were drawn using NUTS(diag_e) at Tue May 22 13:38:43 2018.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
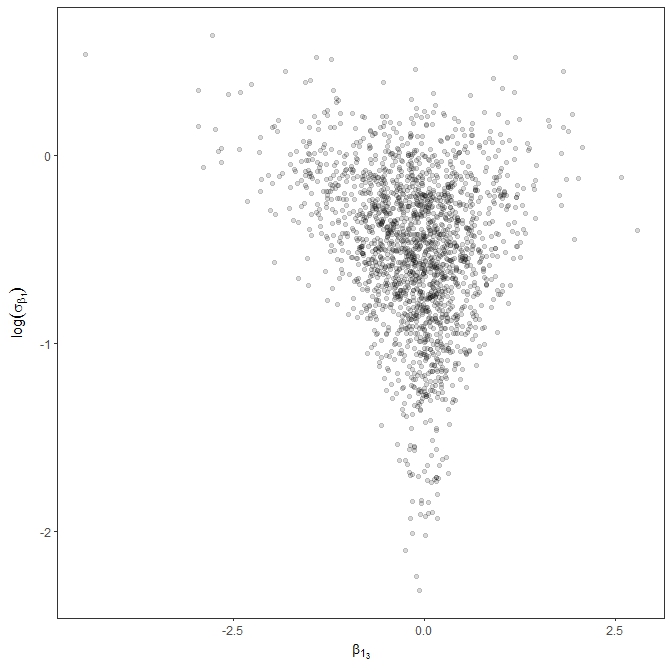
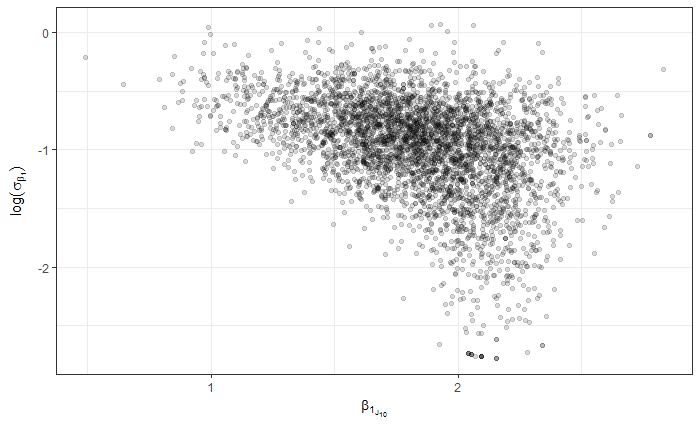
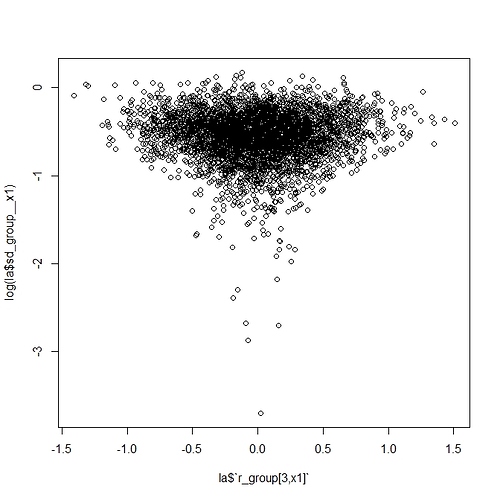
So, all in all, I was hoping maybe I’m missing something with the parameterization or coding that might help me improve the efficiency. I’ll note that the data might be characterized as high N and low p, in the context of Bin( N, p ). For example, the median n_trials is around 16000 and median n_success around 30. So, for p, the vast majority of obs should be much less than p=0.1, but with a few obs as high as 0.8. I’m thinking this is maybe where I’m getting into trouble, but I thought I’d post here to see if there are any glaring errors or other obvious areas for improvement.
Many thanks,
-Roy
Code below:
data{
int<lower=1> N; // number of observations
int<lower=0> y[N]; // n success
int<lower=1> n[N]; // n trials
int<lower=1> J; // n groups
vector[N] x1; // covariate vector: 0/1
int<lower=1, upper=J> group[N]; // indexing J groups to N obs
vector<lower=0>[N] sample_vol; // volume of sample (mL) for gen. quant.
}
parameters{
real b0; // sample-level mean of success (log-odds)
real b1; // sample-level covariate slope
vector[N] eps_z;
matrix[2, J] a_z;
real<lower=0> sigma_z;
vector<lower=0>[2] sigma_a_z;
cholesky_factor_corr[2] L_Omega_J;
}
transformed parameters {
vector[N] p_logit; // success (log-odds)
vector[N] eps; // sample-level error term: eps ~ N(0, sigma)
matrix[J, 2] a; // group-level slopes and intercepts matrix: cbind( \alpha_J , \beta_{1_J} )
vector[J] a_J; // group-level intercepts: \alpha_J
vector[J] b1_J; // group-level slopes: \beta_{1_J}
real<lower=0> sigma; // sample-level sd
vector<lower=0>[2] sigma_a; // group-level sds for intercepts and slopes
cholesky_factor_cov[2] L_Sigma_J; // Chol. cov. matrix for slopes and intercepts
{
sigma = sigma_z * 5; // scaling prior sd
eps = eps_z * sigma; // scaling error term
sigma_a[1] = sigma_a_z[1] * 3; // scale prior for intercepts
sigma_a[2] = sigma_a_z[2] * 3; // scale prior for slopes
L_Sigma_J = diag_pre_multiply(sigma_a, L_Omega_J);
a = (L_Sigma_J * a_z)';
a_J = col(a, 1);
b1_J = col(a, 2);
for (i in 1:N){
p_logit[i] = ( b0 + ( ( b1 + b1_J[group[i]] ) * x1[i] ) + eps[i] ) + a_J[group[i]];
}
}
}
model{
b0 ~ normal( -5 , 3 );
b1 ~ normal( 0 , 5 );
eps_z ~ normal( 0 , 1 );
to_vector(a_z) ~ normal( 0 , 1 );
sigma_z ~ normal( 0 , 1 );
sigma_a_z[1] ~ normal( 0 , 1 ); // \sigma_{\alpha_J}
sigma_a_z[2] ~ normal( 0 , 1 ); // \sigma_{\beta_{1_J}}
L_Omega_J ~ lkj_corr_cholesky(4);
{
target += binomial_logit_lpmf( y | n , p_logit );
}
}
generated quantities{
real p_hat[N];
real conc_hat[N];
real y_hat[N];
real y_new[N];
real conc_new[N];
matrix[2, 2] Omega;
{
Omega = multiply_lower_tri_self_transpose(L_Omega_J);
for ( i in 1:N ) {
p_hat[i] = inv_logit( p_logit[i] );
y_hat[i] = p_hat[i] * n[i];
conc_hat[i] = ( -log( 1 - ( y_hat[i] / n[i] ) ) / 0.00085 ) * ( 1500 / sample_vol[i] );
y_new[i] = binomial_rng( n[i] , p_hat[i] );
conc_new[i] = ( -log( 1 - ( y_new[i] / n[i] ) ) / 0.00085 ) * ( 1500 / sample_vol[i] );
}
}
}