I found one or two example on the website about estimating the ‘mu’ for GMM model, and they set the standard deviation (sigma) equal to a constant. I wonder if I want to estimate the ‘sigma’ for four different Gaussian model, is there any way to do that? What kind of distribution should be assign to ‘sigma’? Should ‘sigma’ also ‘ordered’ as ‘mu’?
Yeah, totally, you can write a model to estimate sigma. There’s always a question of will it work or not :D.
You shouldn’t need an ordering constraint on your sigma parameters. It’s convenient to order the means so that it’s easier to compare posteriors between different chains (so things don’t get swapped). This also assumes each of your different modes needs a different sigma. Do you see this in your data?
To pick a prior for sigma, just pick something on the scale of what you expect the widths of the modes to be. Note you don’t assign any distribution to the posterior of sigma. You can pick a prior but the posterior will probably end up being something else.
Do you have plots of your data? Or the model you are considering?
Hi sorry for the late reply. Recently I am busy with my final exam.
I have the plots of my data.
The first figure is estimation of mux. The purple, red, orange, and green represent the mux values which generate the data. I think it is because of the ‘wrong’ estimation of sigma, the distribution of mux shift to left side. So does the muy distribution. The muy distribution can not find muy=20 (Figure. 2).
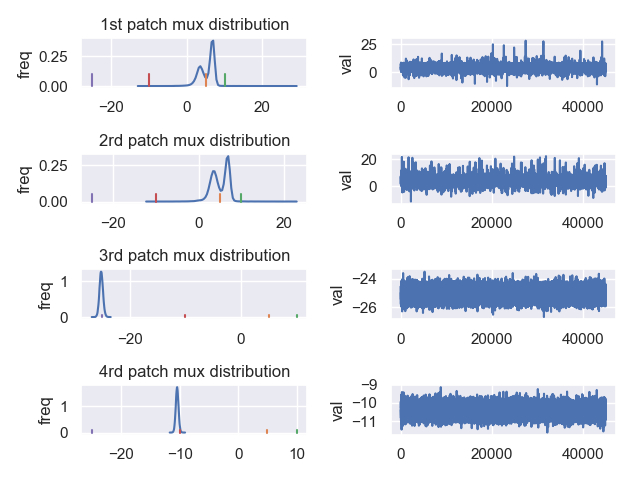

The raw data I used:
The posterior check:
Do you have some specific suggestions to address my concern on sigma estimation? Thanks very much!
Add it as a parameter in your model. Can you post the Stan code? It probably won’t work straight up, but should be easy to add the code to estimate a sigma.
Hi here is the code. I have gave a distribution for sigma, but I don’t think it works well since the estimated sigma value is not similar as the sigma generate the data.
data {
int D; //number of dimensions
int K; //number of gaussians
int N; //number of data
int M; // patch number at time
vector[D] y[N]; // observation data
int O; // prediction day
vector[D] s;//oil spill location
}
parameters {
simplex[K] theta;//mixing proportions
ordered[D] v[K];
positive_ordered[D] p[K];
positive_ordered[D] b[K];
positive_ordered[D] Dif[K];
cholesky_factor_corr[D] L[K]; //cholesky factor of correlation matrix
}
transformed parameters{
vector[D] mu[K];
vector<lower=0>[D] sigma[K]; // standard deviations
for (k in 1:K){
mu[k] = s+v[k]*5;
sigma[k] = 0.05 + sqrt(2*(5)*Dif[k]);}
}
model {
real ps[K];
theta ~ dirichlet(rep_vector(2.0, K));
for (k in 1:K) {p[k] ~ normal(0,10);
v[k] ~ normal(p[k],1);
b[k]~normal(0,1);
Dif[k]~normal(b[k],1);}
for(k in 1:K){
L[k] ~ lkj_corr_cholesky(2);// contain rho
}
for (n in 1:N){
for (k in 1:K){
ps[k] = log(theta[k])+multi_normal_cholesky_lpdf(y[n] | mu[k], diag_pre_multiply(sigma[k],L[k])); //increment log probability of the gaussian
}
target += log_sum_exp(ps);
}
}
generated quantities{
matrix[D,D] Omega[K];
int<lower=0,upper=K> comp[O];
vector[2] ynew[O];
vector[2] munew[K,O];
vector[2] sigmanew[K,O];
matrix[D,D] Sigmanew[K,O];
real<lower=-0.999> ro[K];
for (k in 1:K) {
Omega[k] = multiply_lower_tri_self_transpose(L[k]);
ro[k]=Omega[k,2,1]; }
for (n in 1:M){
for (k in 1:K){
sigmanew[k,n] = 0.05 + sqrt(2*5*Dif[k]);
munew[k,n] = s+v[k]*5;
Sigmanew[k,n] = quad_form_diag(Omega[k], sigmanew[k,n]);
}
}
for (n in 1:M){
comp[n] = categorical_rng(theta);
ynew[n] = multi_normal_rng(munew[comp[n],n],Sigmanew[comp[n],n]);
}
}
'''Hmm, mixture models are often difficult. I’ve not had a lot of fun with GMMs when I’ve tried them, but the way to start this is.
- Fit one normal in 1D with estimated standard deviation
- Fit two normals in 1D with estimated standard deviation
- Fit two normals in 2D with estimated covariance, etc
And just move in bits and pieces step by step.
I didn’t fully dig through the model, but what are each of the parameters doing? p, b, and Dif in particular.

