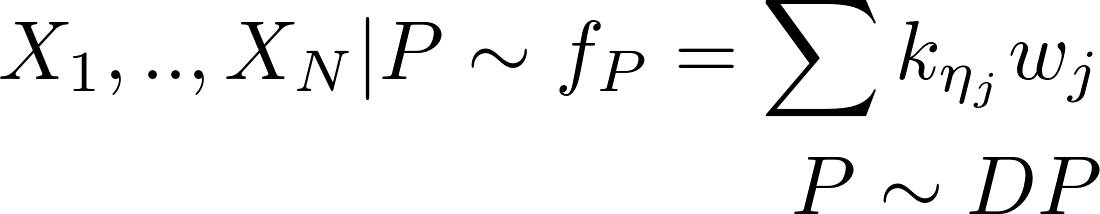Hello,
I would like to implement a DPM model in Stan. My idea was to use the generalized Polya urn algorithm, but in order to do so I need to be able to sample from a mixture of a continuous distribution and a dirac delta. The problem is how to deal with the delta in Stan.
My idea is to approximate it with a normal distribution centred in the support of the delta and with an almost zero variance. How bad is this idea? I am not expert of HMC/MCMC algorithms and I can’t imagine what sampling problems could create this approximation.
Have you any better solution to this problem?
I know that one could implement DPM via stick-breaking (truncated) construction, in this way I can just see the weights and the center of each mixture component, but can’t do clusters analysis! (right?)
Thank you.
1 Like
Sorry this didn’t get answered sooner. I’m not sure what a DPM model is. You can build mixtures of discrete and continuous distributions in Stan in the usual way.
If you try to hack a constant with zero variance normals, Stan has trouble with adapting step sizes—it essentially forces the problem to be ill-conditioned from the get go.
DPM is a Dirichlet Process Model as in the priors used for LDA and other models.
The proposal given here is a bad idea because HMC can’t handle the Dirac delta. You can marginalize out the Dirac which would give you a full mixture model that you can fit in Stan (again, the analogy would be collapsed LDA implementations) but then you’re have to deal with the fact that exchangeable mixture models are terribly ill-posed and Stan’s efficient sampling will just demonstrate how ill-posed they are.
I see—it was the “M” that threw me.
So not just discrete parameters? That you can do in some cases, but if you want to do something like variable selection in a Dirichlet process, it’s going to be combinatorially intractable.
Basically just discrete assignment – the fact that the Dirac might be based at an unknown point can add some more complexity but if you marginalize out enough structure (and assuming some uncertainty on the location of the point mass) then you should end up with a continuous mixture model, albeit one of possibly varying dimensions.
Can you be more detailed in how to do it?
My purpose is clustering, so I need to sample the latent variables (distributed as a DP) in order to have label for my data. It seems to me that if I see my data just as a mixture (so without latent variables), I could use a DP process and find centers and weights of clusters, but can not label my data.
Indeed I can do this way (with stick-breaking):
But it is useless, since no clustering. I need to do in this way:

(Sorry for images size)
You can’t really fit these models with Bayes anyway because of the combinatorial multimodality in the posterior. Stan cant deal with DPs except through approximation. Overall, this whole clustering game runs through heuristics, which is fine for exploratory data analysis.
The manual explains how to code things like LDA up in Stan. Just don’t expect stable Bayesian inference.