Justification for SBC rank uniformity are two:
- theoretical: measure theory that excludes computational/numerical considerations (integration, optimization error)
- experimental: mostly with multivariate normal
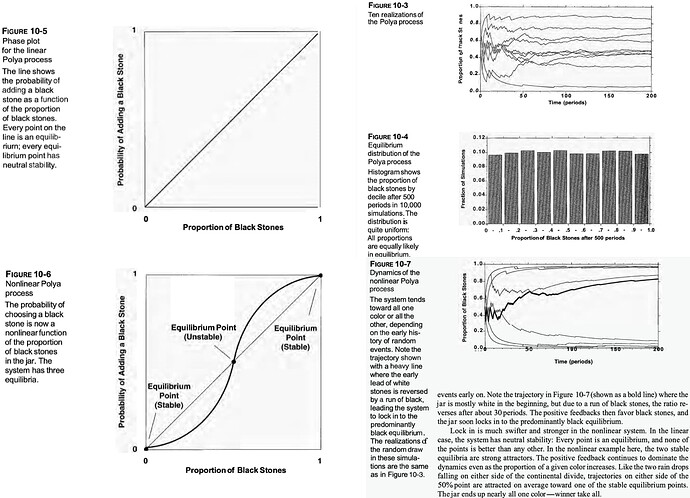
I was curious whether generator’s nonlinearity can impede diagnostics (e.g. ode model). For instance, would rank uniformity equally hold for tight prior near unstable equilibrium point (in fig.10-6)? Could the diverging force in the uni-direction process affect SBC’s self-consistency spirit: prior and posterior are exchangeable conditional on data? Or would SBC be free from these dynamic forces as there exists an honorable screenshot statistical model which cancels out the diverging effect? By screenshot, I mean one version of the statistical model used for data generation and parameter estiamtion, which ideally aggregates across time within a specific length of time window in the process. For instance, we can imagine some representable statistical model within every five periods of time from fig.10-7 where diverging effect is relatively less prominent.
To be honest, the fact that nonlinearity can impede outcome rank uniformity in polya urn model, motivated this post. Compared to linear model where the probability of balls added in each run is linearly proportional to the current proportion which results in uniform rank as in fig.10-3, the nonlinear polya process disrupts this uniformity as in fig.10-7. Aside from numeric issues from integration and optimization approximation (i.e. stuck or inconsistent target density evaluation or its gradient), I am curious whether there exist deeper mechanisms forbidding \theta, \theta' symmetry in \pi(\theta, y, \theta') from this post which delves into SBC proof. Figure’s source is chp.10 path dependence from Business Dynamics.
Note.1. A similar question was asked in Simulation Based Calibration (SBC) for non-linear model. I think is worth revisiting from a specific polya process context and the philosophy of iteration of simulation-based calibration and calibration-based simulation approximate joint space of simulate and calibrate function.
Note.2. I wonder whether the raised question can be sidestepped by considering specific verification procedures for stochastic process e.g. this paper on sbc for gaussian process. There are two pieces to this question: i) does unstable equilibrium point affect their method ii) if not, could we view their model to be rightly calibrated? (statically calibrated, but not dynamically calibrated perhaps)