Compositional Data Dirichlet Regression Question

Modeling
1

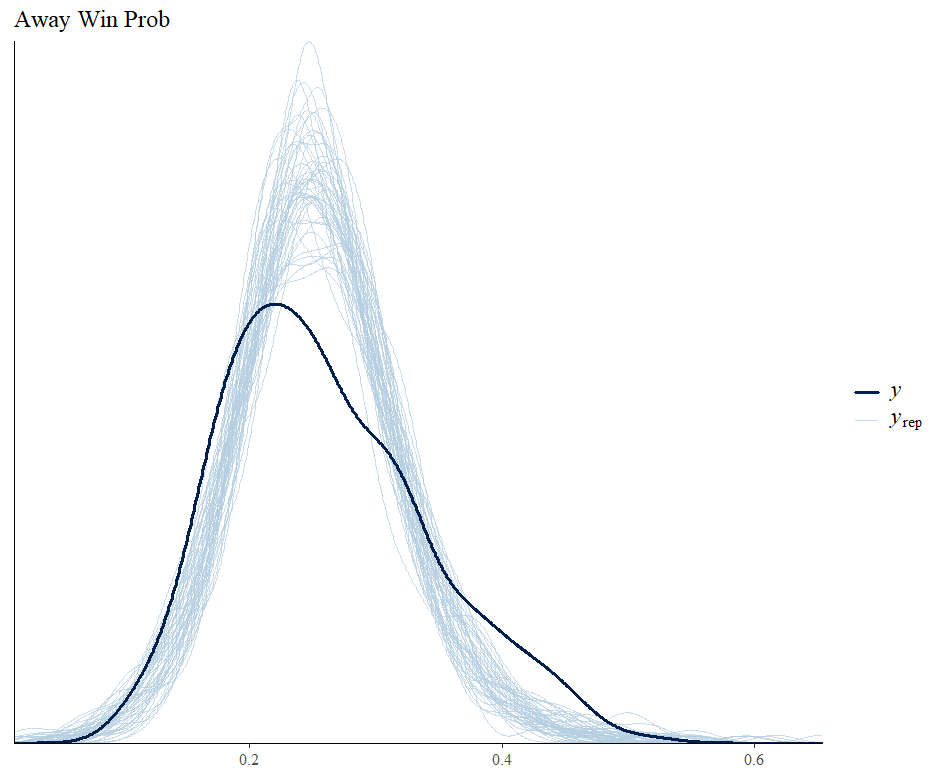
I am working on a soccer model that takes in the home and away team, and outputs the sportsbook betting odds for home team winning, away team winnings, or draw. This is compositional dataset where the outcome probabilities sum to 1. I am using a hierarchical Dirichlet regression, which you can see below.

data {
  int<lower=0> N; // number of rows
  int<lower=0> J; // number of teams
  simplex[3] y[N]; // outcome matrix
  int<lower=0, upper = J> home_team[N]; // home team id
  int<lower=0, upper = J> away_team[N]; // away team id
}

parameters {
  vector[3] beta0; // intercepts
  vector[J] beta; // beta's for each team
  real<lower = 0> sigma_teams; // sigma for pooling

}

model {

  vector[N] alpha1;
  vector[N] alpha2;
  vector[N] alpha3;

  beta0[1] ~ normal(3, 2);
  beta0[2] ~ normal(2, 2);
  beta0[3] ~ normal(2, 2);
  beta ~ normal(0, sigma_teams);
  sigma_teams ~ cauchy(0, 2);

  for (i in 1:N) {
    alpha1[i] = exp(beta0[1] + beta[home_team[i]] + beta[away_team[i]]);
    alpha2[i] = exp(beta0[2] + beta[home_team[i]] + beta[away_team[i]]);
    alpha3[i] = exp(beta0[3] + beta[home_team[i]] + beta[away_team[i]]);
  }

  for (i in 1:N) {
    y[i] ~ dirichlet([alpha1[i], alpha2[i], alpha3[i]]);
  }

}

generated quantities {
  simplex[3] y_rep[N]; // replicated outcomes

  vector[N] alpha1;
  vector[N] alpha2;
  vector[N] alpha3;
[mls_bm_odds_csv.csv|attachment](upload://pGDotk696kzkqNxpKcijWBpBiZo.csv) (29.5 KB)

  for (i in 1:N) {
    alpha1[i] = exp(beta0[1] + beta[home_team[i]] + beta[away_team[i]]);
    alpha2[i] = exp(beta0[2] + beta[home_team[i]] + beta[away_team[i]]);
    alpha3[i] = exp(beta0[3] + beta[home_team[i]] + beta[away_team[i]]);
  }

  for (i in 1:N) {
    vector[3] alpha;
    alpha[1] = alpha1[i];
    alpha[2] = alpha2[i];
    alpha[3] = alpha3[i];
    y_rep[i] = dirichlet_rng(alpha);
  }
}

The issue is that while home and away win prob have roughly the same standard deviation, draw prob has a very tight standard deviation. I think this is what causes my posterior predictive checks to look bad.

dir_home_pp
dir_home_pp942×777 20.9 KB

draw_pp
draw_pp942×777 14.4 KB

away_pp
away_pp942×777 22.8 KB

I don’t have much experience with this type of regression, so any help would be appreciated. For reference, I added the model code and data. Thanks!
mls_implied_odds_model.R (1.7 KB)
mls_bm_odds_csv.csv (29.5 KB)

2

Hi, @dgerth5 and sorry I didn’t see this sooner to answer.

I think your problem is due to adding the abilities in the Dirichlet parameters. What I would think you’d want is something like this, which has the home team (plus home team advantage) vs away team vs. draw, where draw is a new parameter:

for (n in 1:N) {
  vector[3] log_alpha = [beta[home[n]] + home_advantage,
                         beta[away[n]],
                         draw]';
  y[n] ~ dirichlet(exp(log_alpha));
}

Abilities and draws could be set up as regressions if there are covariates. For example, the inverse of absolute difference between home and away ability may influence probability of draw, so you could set it up to be something like draw = gamma / abs(home-ability - away-ability), where gamma is a new parameter.

Home advantage could also vary by team if you have enough data to estimate it.

2 Likes